Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.5 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.5
Question 1.
Solve the following systems of linear equations by Gaussian elimination method:
(i) 2x – 2y + 3z = 2, x + 2y – z = 3, 3x – y + 2z = 1
Solution:
Augmented matrix

Writing the equivalent equations from echelon from.
x – y + 2z = 3 …………. (1)
5y – 6z = -4 ………….. (2)
-z = -4
z = 4
(2) ⇒ 5y – 6z = -4
5y – 24 = -4
5y = -4 + 24
5y = 20
y = 4
(1) ⇒ x – y + 2z = 3
x – 4 + 8 = 3
x = 3 + 4 – 8
x = -1
∴ x = -1, y = 4, z = 4
![]()
(ii) 2x + 4y + 6z = 22, 3x + 8y + 5z = 27, -x + y + 2z = 2.
Solution:
Augmented matrix

Writing the equivalent equations from echelon from.
x + 2y + 3z = 11 …………. (1)
y – 2z = -3 ………….. (2)
11z = 22
z = 2
(2) ⇒ y – 2z = -3
y – 4 = -3
y = -3 + 4
y = 1
(1) ⇒ x + 2y + 3z = 11
x + 2(1) + 3(2) = 11
x + 2 + 6 = 11
x = 11 – 8 = 3
∴ x = 3, y = 1, z = 2
![]()
Question 2.
If ax² + bx + c is divided by x + 3, x – 5, and x – 1, the remainders are 21, 61 and 9 respectively. Find a, b and c. (Use Gaussian elimination method.)
Solution:
Given: f(x) = ax² + bx + c
In Remainder Theorem
f(-3) = 21
a(-3)² + b(-3) + c = 21
9a – 3b + c = 21 ……….. (1)
f(5) = 61
25a + 5b + c = 61 …………. (2)
f(1) = 9
a + b + c = 9 ………… (3)
Augmented matrix
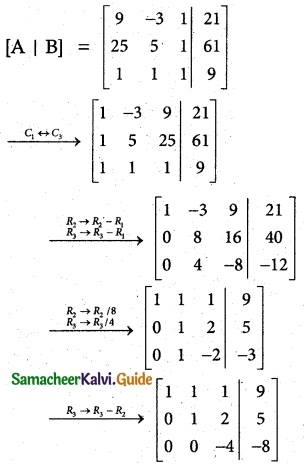
Writing the equivalent equations from echelon from.
a + b + c = 9 …………. (1)
b + 2c = 5 ………….. (2)
-4c = -8
c = 2
(2) ⇒ b + 2c = 5
b + 4 = 5
b = 5 – 4
b = 1
(1) ⇒ a + b + c = 9
a + 1 + 2 = 9
a = 9 – 3
a = 6
a = 6, b = 1, c = 2
![]()
Question 3.
An amount of Rs 65,000 is invested in three bonds at the rates of 6%, 8% and 10% per annum respectively. The total annual income is Rs 5,000. The income from the third bond is Rs 800 more than that from the second bond. Determine the price of each bond. (Use Gaussian elimination method.)
Solution:
Let the amounts of 3 bounds be x, y, z
x + y + z = 65,000

Writing the equivalent equations from echelon from.
x + y + z = 65000 …………. (1)
2y + 3z = 90000 ………….. (2)
21z = 42000
z = 20000
(2) ⇒ 2y = 90000 – 3 × 20000
2y = 30000
y = 15000
(1) ⇒ x + 15000 + 20000 = 65000
x = 30000
∴ x = 30000, y = 15000, z = 20000
![]()
Question 4.
A boy is walking along the path y = ax² + bx + c through the points (-6, 8),(-2, -12), and (3, 8). He wants to meet his friend at P(7, 60). Will he meet his friend? (Use Gaussian elimination method.)
Solution:
y = ax² + bx + c
At(-6, 8) ⇒ 8 = 36a – 6b + c ………… (1)
At(-2, -12) ⇒ -12 = 4a – 2b + c ………… (2)
At(3, 8) ⇒ 8 = 9a + 3b + c ………… (3)
Augmented matrix

Writing the equivalent equations from the echelon.
36a – 6b + c = 8 …………. (1)
3b – 2c = 29 ………….. (2)
5c = -50
c = -10
(2) ⇒ 3b – 2c = 29
3b – 20 = 29
3b = 9
b = 3
(1) ⇒ 36a – 18 – 10 = 8
36a = 8 + 18 + 10
36a = 36
a = 1
At P (7, 60), y = ax² + bx + c
60 = 1(7²) + 3(7) – 10
60 = 49 – 21 – 10
60 = 60
He will meet his friend at P (7, 60)
![]()