Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.7 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.7
Question 1.
Solve the following system of homogeneous equations.
(i) 3x + 2y + 7z = 0; 4x – 3y – 2z = 0; 5x + 9y + 23z = 0
Solution:
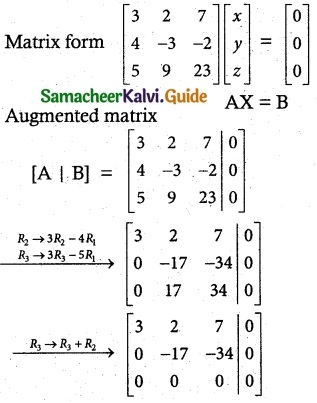
ρ(A) = 2 ρ[A | B] = 2
ρ(A) ρ[A | B] = 2 < n
The system is consistent. It has non trivial solution.
Writing the equivalent equations from echelon form
3x + 2y + 7z = 0 ………… (1)
-17y – 34z = 0 ……….. (2)
Put z = t
(2) ⇒ -17y = 34t
y = \(\frac {34t}{-17}\) = -2t
(1) ⇒ 3x + 2(-2t) + 7t = 0
3x – 4t + 7t = 0
3x + 3t = 0
3x = -3t
x = -t
(x, y, z) (-t, -2t, t) ∀ t ∈ R
![]()
(ii) 2x + 3y – z = 0, x – y – 2z = 0, 3x + y + 3z = 0
Solution:

ρ(A) = 3 ρ[A | B] = 3
ρ(A) = ρ[A | B] = 3
The system is consistent. It has trivial solution.
x = 0, y = 0, z = 0
![]()
Question 2.
Determine the values of λ for which the following system of equations.
x + y + 3z = 0; 4x + 3y + λz = 0, 2x + y + 2z = 0 has
(i) a unique solution
(ii) a non-trivial solution.
Solution:
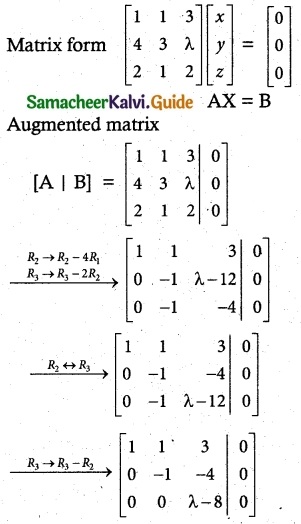
Case (i):
if λ ≠ 8
ρ(A) = 3 ρ(A | B) = 3
ρ(A) = ρ(A | B) = 3 = n
The system is consistent. It has unique (trivial) solution.
∴ Solution x = 0, y = 0, z = 0
Case (ii):
if λ = 8
ρ(A)= ρ(A | B) = 2
ρ(A) = ρ(A | B) = 2 < n
The system is consistent. It has non trivial solution.
![]()
Question 3.
By using Gaussian elimination method, balance the chemical -reaction equation:
C2H6 + O2 → H2O + CO2.
Solution:
We are searching for positive integers x1, x2, x3 and x4
x1 C2H6 + x2 O2 → x3 H2O + x4 CO2 ……….(1)
The number of carbon atoms on the LHS of (1) should be equal to the number of carbon atoms on the RHS of (1) so we get a linear
homogeneous equation.
2x1 x4 = 2x1 – x4 = 0 ……..(2)
6x1 = 2x3 = 6x1 – 2x3 = 0
÷ 2 ⇒ 3x1 – x3 = 0 ………(3)
2x2 = x3 + 2x4 ⇒ 2x2 – x3 – 2x4 = 0 ……… (4)
Equation (2), (3) and (4) constitute a homogeneous system of linear equations in four unknowns.
Augmented matrix

The system is consistent and has an infinite number of solutions.
Writing the equations using the echelon form we get
-2x3 + 3x4 = 0 ……….. (1)
2x2 – x3 – 2x4 = 0 ………… (2)
2x1 – x4 = 0 …………. (3)
Put x4 = t
(3) ⇒ 2x1 – t = 0
x1 = \(\frac {t}{2}\)
(1) ⇒ -2x3 + 3x4 = 0
-2x3 = -3t
x3 = \(\frac {3}{2}\) t
(2) ⇒ 2x2 – x3 – 2x4 = 0
2x2 – \(\frac {3}{2}\) t – 2t = 0
2x2 = \(\frac {3}{2}\) t + 2t = \(\frac {7t}{2}\)
x2 = \(\frac {7t}{4}\)
(x1, x2, x3, x4) = (\(\frac {t}{2}\), \(\frac {7t}{4}\), \(\frac {3}{2}\)t, t) ∀ t ∈ R
since x1, x2, x3 and x4 are positive integers.
Let us choose t = 4

So the balanced equation is
2C2H6 + 7O2 → 6H2O + 4CO2.
![]()