Samacheer Kalvi 12th Maths Guide Chapter 10 Ordinary Differential Equations Ex 10.6

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 Ordinary Differential Equations Ex 10.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.6

Question 1.
Solve the following differential equations.
[x + y cos(\(\frac { y }{ x }\))] dx = x cos (\(\frac { y }{ x }\)) dy
Solution:
The given equation can be written as

On integration we obtain

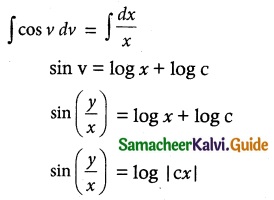
which gives the required solution.

Question 2.
Solve (x³ + y³)dy – x² ydx = 0
Solution:
The given equation can be written as

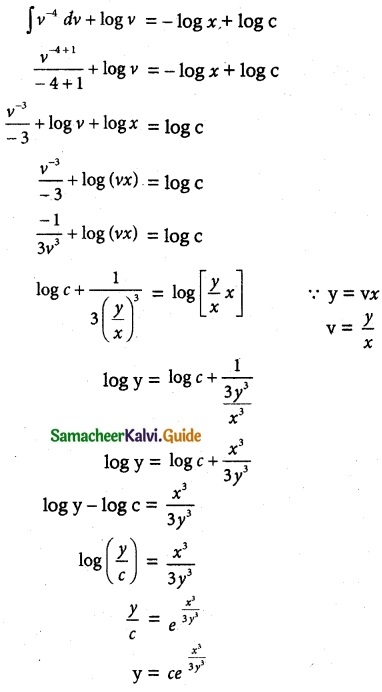
Question 3.
Solve ye^{\(\frac { x }{ y }\)} dx = (x^{\(\frac { x }{ y }\)} + y)dy
Solution:
The given equation can be written as

Question 4.
Solve 2xy dx + (x² + 2y²)dy = 0
Solve ye^{\(\frac { x }{ y }\)} dx = (x^{\(\frac { x }{ y }\)} + y)dy
Solution:
The given differential equation can be written as


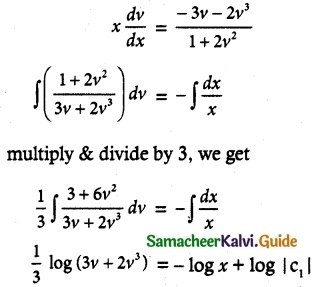
\(\frac { 1 }{ 3 }\) log (3v + 2v³) + log x = log |C₁|
log (3v + 2v³) + 3log (x) = 3 log (C₁)
log (3v + 2v³) + log (x)³ = log (C₁)³
log (3v + 2v³)x³ = log C₁³
(3v + 2v³)x³ = C₁³

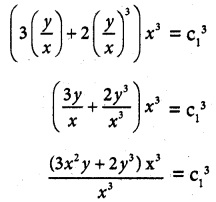
3x²y + 2y³ = C₁³
3x²y + 2y³ = C is a required solution.

Question 5.
(y² – 2xy) dx = (x² – 2xy) dy
Solution:
Given equation is (y² – 2xy) dx = (x² – 2xy) dy
y² – 2xy = (x² – 2xy) \(\frac { dy }{ dx }\)
∴ The equation can written as


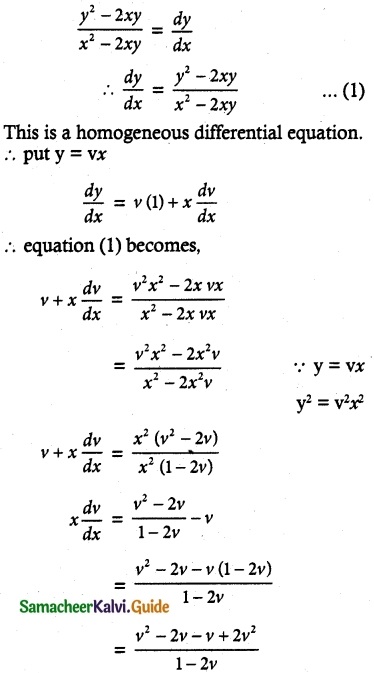
log (3v² – 3v) = – 3 log x + log C
log (3v² – 3v) = – log x³ + log C
= log c – log x³

Question 6.
x \(\frac { dy }{ dx }\) = y – x cos²(\(\frac { y }{ x }\))
Solution:
Given x \(\frac { dy }{ dx }\) = y – x cos² \(\frac { y }{ x }\)
The equation can be written as
\(\frac { dy }{ dx }\) = \(\frac { y-cos^2 \frac { y }{ x } }{ x }\) …….. (1)
This is a homogeneous differential equation.
y = vx
\(\frac { dy }{ dx }\) = v (1) + x \(\frac { dv }{ dx }\)
Substituting \(\frac { dy }{ dx }\) value in equation (1), we get

Integrating on both sides, we get
∫ sec² v dx = -∫ \(\frac { dx }{ x }\)
tan v = – log x + log C
tan v = log C – log x
tan v = log(\(\frac { C }{ x }\))
e^{tan v} = \(\frac { C }{ x }\)
C = x e^{tan v}
C = x e^{tan \(\frac { y }{ x }\)}
Is a required equation.

Question 7.
Solve (1 + 3e^{\(\frac { y }{ x }\)}) dy + 3e^{tan \(\frac { y }{ x }\)} (1 – \(\frac { y }{ x }\)) dx = 0, given that y = 0 when x = 1.
Solution:
The given differential equation may be


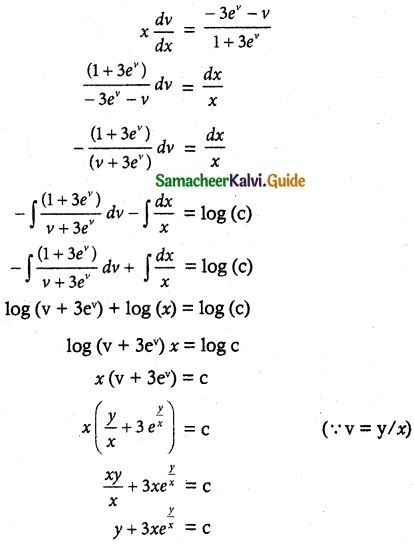
Given that y = 0 when x = 1
0 + 3(1) e° = c
3 = c
∴ y + 3xe^y/x = 3 is a required solution.

Question 8.
(x² + y²) dy = xy dx. It is given that y (1) = y(x₀) = e. Find the value of x₀.
Solution:
The given differential equation is of the form
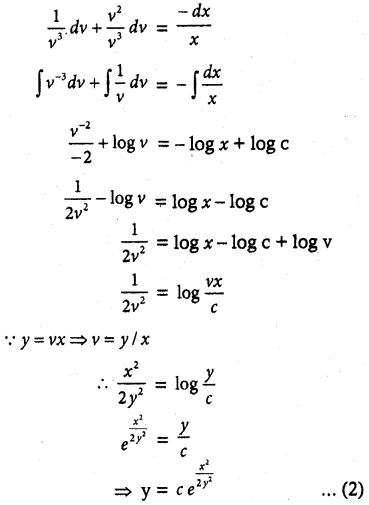
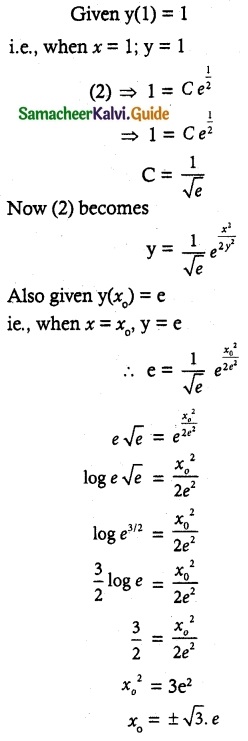