Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 11 Probability Distributions Ex 11.4 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 11 Probability Distributions Ex 11.4
Question 1.
For the random variable X with the given prob-ability mass function as below, find the mean and variance.

Solution:


Var(X)= E(X²) – [E(X)]²
= 8.1 – (2.3)²
= 8.1 – 5.29
= 2.81

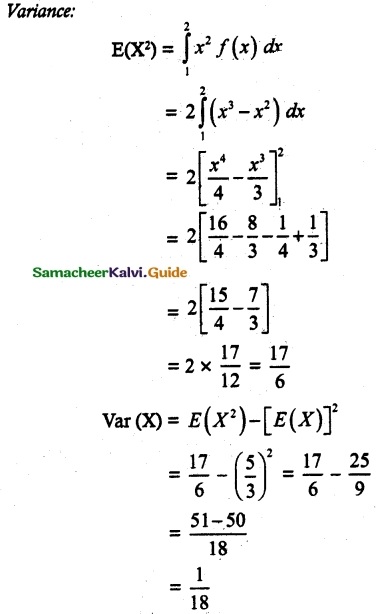
Var (X) = E(X²) – [E(X)]²
= 3.33 – (1.67)²
= 3.33 – 2.79
= 0.54
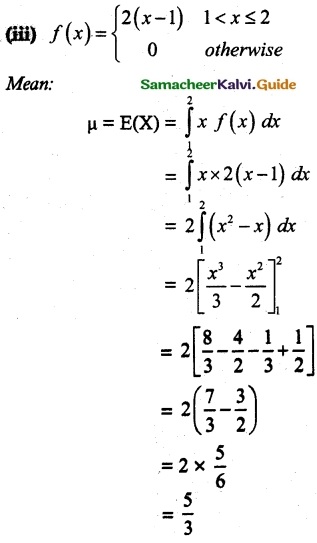

Var (X) = E(X²) – [E(X)]²
= 8 – 4
= 4
![]()
Question 2.
Two balls are drawn in succession without replacement from an urn containing four red balls and three black balls. Let X be the possible outcomes drawing red balls. Find the probability mass function and mean for X.
Solution:
Let X be the random variable that denotes the number of red balls.
X = {0, 1, 2}
Sample space consist of 7C2 = 21
X= 0, X-1 (BB) = 3C2
X= 1, X-1 (BR) = 3C1 × 4C1 = 12
X = 2, X-1 (RR) 4C2 = 6

![]()
Question 3.
If µ and σ² are the mean and variance of the discrete random variable X and E(X + 3) = 10 and E(X + 3)² = 116, find µ and σ²
Solution:
Given E(X + 3) = 10
E(aX + b) = aE(X) + b
E(X + 3) = 10 ⇒ E(X) + 3 = 10
⇒ µ = E(X) = 7
E(X + 3)² = 116
E(X² + 6X + 9) = 116
E(X²) + 6E(X) + 9 = 116
E(X²) + 6(7) + 9 = 116
E(X²) = 65
σ² = Var (X) = E(X²) – [E(X)]²
= 65 – 49
= 16
![]()
Question 4.
Four fair coins are tossed once. Find the probability mass function, mean and variance for a number of heads that occurred.
Solution:
Let X be the random variable that denotes the number of heads when four coins are tossed once.
X ={0, 1, 2, 3}
n(S) = 16
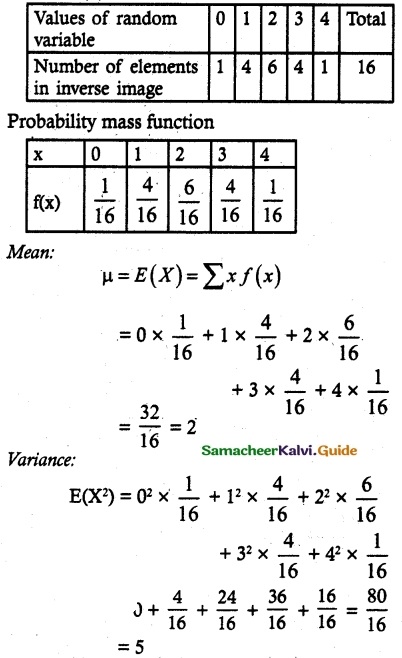
Var (X) = E(X²) – [E(X)]²
= 5 – 4
= 1
![]()
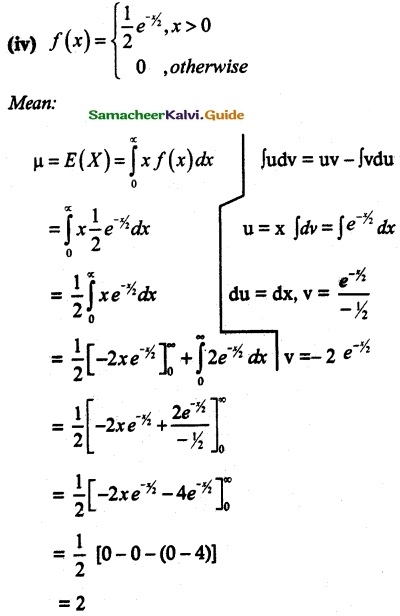
Question 5.
A commuter train arrives punctually at a station every half hour. Each morning, a student leaves his house to the train station. Let X denote the amount of time, in minutes, that the student waits for the train from the time he reaches the train station. It is known that the pdf of X is
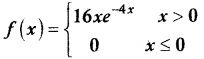
Obtain and interpret the expected value of the random variable X.
Solution:
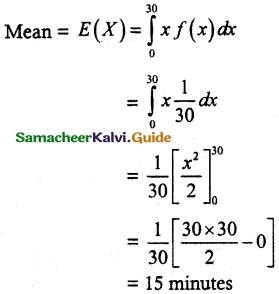
The average waiting time for the student is 15 minutes.
![]()
Question 6.
The time to failure in thousands of hours of an electronic equipment used in a manufactured computer has the density function
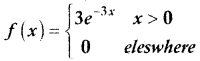
Find the expected life of this electronic equipment.
Solution:
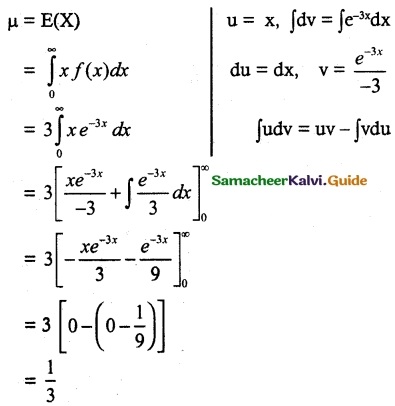
Expected life of the electronic equipment = \(\frac { 1 }{ 3 }\)
![]()
Question 7.
The probability density function of the random variable X is given by
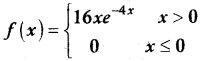
find the mean and variance of X.
Solution:
Mean:

Var (X) = E(X²) – [E(X)]²
\(\frac { 3 }{ 8 }\) – \(\frac { 1 }{ 4 }\)
= \(\frac { 1 }{ 8 }\)
![]()
Question 8.
A lottery with 600 tickets gives one prize of Rs 200, four prizes of Rs 100 and six prizes of Rs 50. If the ticket costs is Rs 2, find the expected winning amount of a ticket.
Solution:
Let X be the random variable denotes the amount win in the lottery
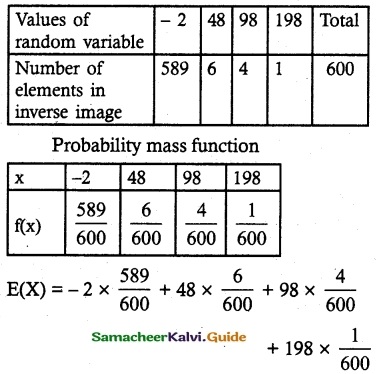
= 0.5
Loss = Rs 0.5
![]()