Samacheer Kalvi 12th Maths Guide Chapter 11 Probability Distributions Ex 11.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 11 Probability Distributions Ex 11.5 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 11 Probability Distributions Ex 11.5

Question 1.
Compute P(X = k) for the binomial distribution, B(n, p) where
(i) n = 6, p = \(\frac { 1 }{ 3 }\), k = 3
(ii) n = 10, p = \(\frac { 1 }{ 5 }\), k = 4
(iii) n = 9, p = \(\frac { 1 }{ 2 }\), k = 7
Solution:

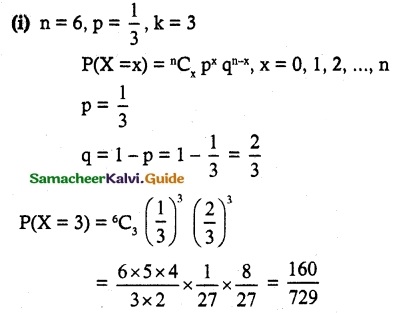
Question 2.
The probability that Mr. Q hits a target ait any trial is \(\frac { 1 }{ 4 }\). Suppose he tries at the target 10 times. Find the probability that he hits the target (i) exactly 4 times (ii) atleast one time
Solution:
Let p be the probability of hitting the target
n = 10, p = \(\frac { 1 }{ 4 }\), X ~ B(n, p)
P(X = x) = ⁿC_x p^x q^n-x, x = 0, 1, 2, …. n
q = 1 – p = \(\frac { 3 }{ 4 }\)
(i) Probability of hitting the target exactly 4 times

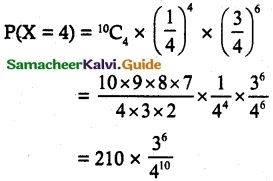
(ii) Probability of hitting atleast one time
P(X ≥ 1) = 1 – P(X < 1) = 1 – P(X = 0)
= 1 – ¹⁰C₀ × (\(\frac { 1 }{ 4 }\))° × (\(\frac { 3 }{ 4 }\))¹⁰
= 1 – \(\frac { 3^{10} }{ 4^{10} }\)

Question 3.
Using binomial distribution find the mean and variance of X for the following experiments
(i) A fair coin is tossed 100 times and X denotes the number of heads.
(ii) A fair die is tossed 240 times and X denotes the number of times that four appeared.
Solution:
(i) Let p be the probability of getting heads
⇒ p = \(\frac { 1 }{ 2 }\)
n = 100, p = \(\frac { 1 }{ 2 }\), X ~ B(n, p)
q = 1 – p = \(\frac { 1 }{ 2 }\)
Mean = np
= 100 × \(\frac { 1 }{ 2 }\)
= 50
Variance = npq
= 50 × \(\frac { 1 }{ 2 }\)
= 25

(ii) Let p be the probability of getting 4 when a die is thrown
n = 240, p = \(\frac { 1 }{ 6 }\), X ~ B(n, p)
q = 1 – p = \(\frac { 5 }{ 6 }\)
Mean = np
= 240 × \(\frac { 1 }{ 6 }\) = 40
Variance = npq
= 40 × \(\frac { 5 }{ 6 }\) = \(\frac { 100}{ 3 }\)

Question 4.
The probability that a certain kind of component will survive a electrical test is \(\frac { 3 }{ 4 }\). Find the probability that exactly 3 of the 5 components tested survive.
Solution:
Let p be the probability of a certain component survive in an electrical test.
n = 5, p =\(\frac { 3 }{ 4 }\), X ~ B(n, p), k = 3
q = 1 – p = \(\frac { 1 }{ 4 }\)
P(X = x) = ⁿC_x p^x q^n-x, x = 0, 1, 2, …. n

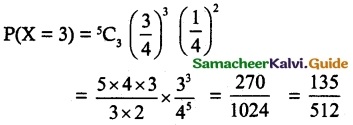
Question 5.
A retailer purchases a certain kind of electronic, device from a manufacturer. The manufacturer indicates that the defective rate of the device 5 is 5%. The inspector of the retailer randomly picks 10 items from a shipment. What is the probability that there will be
(i) atleast one defective item
(ii) exactly two defective items?
Solution:
Let p be the probability that indicates the defective rate of an electronic device
p = 5%
= 0.05
q = 1 – p = 0.95
n = 10, p = 0.05, X ~ B(n, p)
P(X = x) = ⁿC_x p^x q^n-x, x = 0, 1, 2, …. n
(i) Atleast 1 defective item
P(X ≥ 1) = 1 – (X < 1)
= 1 – P(X = 0)
= 1 – ¹⁰C₀ (0.05)° (0.95)¹⁰
= 1 – (0.95)¹⁰

(ii) Exactly two defective items
P(X = 2) = ¹⁰C₂ (0.05)² (0.95)⁸

Question 6.
If the probability that fluorescent light has a useful life of atleast 600 hours is 0.9, find the probabilities that among 12 such lights
(i) exactly 10 will have a useful life of atleast 600 hours
(ii) At atleast 11 will have a useful life of atleast 600 hours
(iii) At atleast 2 will not have a useful life of at least 600 hours.
Solution:
Let p be the probability of the useful life hours of a fluorescent light.
n = 12, p = 0.9, X ~ B(n, p)
q – 1 – p = 0.1
P(X = x) = ⁿC_x p^x q^n-x, x = 0, 1, 2, …. n
(i) Exactly 10
P(X = 10) = ¹²C₁₀ (0.9)¹⁰ (0.1)²

(ii) Atleast 11
P(X ≥ 11) = P(X = 11) + P(X = 12)
= ¹²C₁₁ (0.9)¹¹ (0.1)¹ + ¹²C₁₂ (0.9)¹² (0.1)°
= 12 × (0.9)¹¹ × 0.1 + 1 × (0.9)¹² × 1
= (0.9)¹¹ (12 × 0.1 × 0.9)
= (0.9)¹¹ (1.2 + 0.9)
= (2.1) (0.9)¹¹

(iii) Atleast 2 will not have a useful
P(X ≤ 10) = 1 – P(X > 10)
= 1 – [P(X = 11) + P(X = 12)]
= 1 – (2.1)(0.9)¹¹

Question 7.
The mean and standard deviation of a binomial variate X are respectively 6 and 2. Find
(i) The probability mass function
(ii) P(X = 3)
(iii) P(X ≥ 2).
Solution:
X ~ B(n, p)
Given, Mean = 6, Standard deviation = 2
np = 6, \(\sqrt { npq }\) = 2
npq = 4
\(\frac { npq }{ np }\) = \(\frac { 4 }{ 6 }\)
q = \(\frac { 2 }{ 3 }\)
p = 1 – q = \(\frac { 1 }{ 3 }\)
npq = 4
n × \(\frac { 1 }{ 3 }\) × \(\frac { 2 }{ 3 }\) = 4
n = 18
(i) Probability mass function
P(X = x) = ⁿC_x p^x q^n-x, x = 0, 1, 2, …. n

Question 8.
If X ~ B(n, p) such that 4P(X = 4) = P(x = 2) and n = 6. Find the distribution, mean and standard deviation of X.
Solution:
X ~ B(n, p)
Given, 4P(X = 4) = P(X = 2), n = 6
P(X = x) = ⁿC_x p^x q^n-x, x = 0, 1, 2, …. n
⇒ 4 ⁶C₄ p⁴ q² = ⁶C₂ p² q⁴
⇒ 4 p² = q²
4 (1 – q)² = q²
4(1 – 2q + q²) = q²
3q² – 8q + 4 = 0
(q – 2) (3q – 2) = 0
q = \(\frac { 2 }{ 3 }\) (q ≠ 2)
Distribution
P(X = x) = ⁶C_x (\(\frac { 1 }{ 3 }\))^x (\(\frac { 2 }{ 3 }\))^6-x
x = 0, 1, 2, 3, 4, 5, 6
Mean = np = 6 × \(\frac { 1 }{ 3 }\) = 2
Variance = npq = 2 × \(\frac { 2 }{ 3 }\) = \(\frac { 4 }{ 3 }\)

Question 9.
In a binomial distribution consisting of 5 independent trials, the probability of 1 and 2 successes are 0.4096 and 0.2048 respectively. Find the mean and variance of the random variable.
Solution:
n = 5, X ~ B(n, p)
Given, P(X = 1) = 0.4096
P(X = 2) = 0.2048
P(X = x) = ⁿC_x p^x q^n-x, x = 0, 1, 2, …. n
⇒ ⁵C₁ p q⁴ = 0.4096
⇒ ⁵C₂ p² q³ = 0.2048
5 p q⁴ = 0.4096 …….. (1)
10 p² q³ = 0.2048 ………. (2)
(1) divided by (2),
⇒ \(\frac { 5pq^4 }{ 10p^2q^3 }\) = 2
\(\frac { p }{ q }\) = 4
q = 4p
q = 4 (1 – q)
q = 4 – 4q
5q = 4
q = \(\frac { 4 }{ 5 }\)
p = 1 – q = \(\frac { 1 }{ 5 }\)
Mean = np
= 5 × \(\frac { 1 }{ 5 }\) = 1
Variance = npq
= 1 × \(\frac { 4 }{ 5 }\) = \(\frac { 4 }{ 5 }\)
Distribution
P(X = x) = ⁵C_x (\(\frac { 1 }{ 5 }\))^x (\(\frac { 4 }{ 5 }\))^5-x
x = 0, 1, 2, 3, 4, 5.