Samacheer Kalvi 12th Maths Guide Chapter 12 Discrete Mathematics Ex 12.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 12 Discrete Mathematics Ex 12.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.1

Question 1.
Determine whether * is a binary operation on the sets-given below
(i) a * b – a. |b| on R
(ii) a * b = min (a, b) on A = {1, 2, 3, 4, 5}
(iii) (a * b) = a√b is binary on R
Solution:
(i) Yes.
Reason: a, b ∈ R. So, |b| ∈ R when b ∈ R
Now multiplication is binary on R
So a|b| ∈ R when a, b ∈ R.
(Le.) a * b ∈ R.
* is a binary operation on R.

(ii) Yes.
Reason: a, b ∈ R and minimum of (a, b) is either a or b but a, b ∈ R.
So, min (a, b) ∈ R.
(Le.) a * b ∈ R.
* is a binary operation on R.

(iii) a* b = \(a \sqrt{b}\) where a, b ∈ R.
No. * is not a binary operation on R.
Reason: a, b ∈ R.
⇒ b can be -ve number also and the square root of a negative number is not real.
So \(\sqrt{b}\) ∉ R even when b ∈ R.
So \(\sqrt{b}\) ∉ R. ie., a * b ∉ R.
* is not a binary operation on R.

Question 2.
On Z, define ⊗ by (m ⊗ n) =mⁿ + n^m: ∀m, n ∈ Z Is ⊗ binary on Z?
Solution:
No. * is not a binary operation on Z.
Reason: Since m, n ∈ Z.
So, m, n can be negative also.
Now, if n is negative (Le.) say n = -k where k is +ve.

Similarly, when m is negative then n^m ∉ Z.
∴ m * n ∉ Z. ⇒ * is not a binary operation on Z.

Question 3.
Let * be defined on R by (a * b) = a + b + ab – 7. Is * binary on R? If so, find 3 * (\(\frac { -7 }{ 15}\))
Solution:
(a * b) = a + b + ab – 7 ∀ a, b ∈ R
If a ∈ R, b ∈ R then ab ∈ R
∴ (a * b) = a + b + ab – 7 ∈ R
For example, let 1, 2 ∈ R
(1 * 2) = 1 + 2 + (1)(2) – 7
= -2 ∈ R
∴ * is a binary operation on R

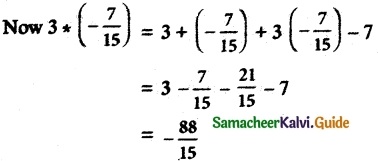
Question 4.
Let A = {a + √5 b: a, b ∈ Z}. Check whether the usual multiplication is a binary operation on A.
Solution:
Let A = a + \(\sqrt{5}\) b and B = c + \(\sqrt{5}\)d, where a, b, c, d ∈ M.
Now A * B ={a + \(\sqrt{5}\)b)(c + \(\sqrt{5}\)d)
= ac + \(\sqrt{5}\)ad + \(\sqrt{5}\)bc + \(\sqrt{5}\)b\(\sqrt{5}\)d
= (ac + 5bd) + \(\sqrt{5}\)(ad+ bc) ∈ A
Where a, b, c, d ∈ Z
So * is a binary operation.

Question 5.
(i) Define an operation * on Q as follows:
a * b = (\(\frac { a+b }{ 2}\)); a, b ∈ Q. Examine the closure, commutative and associate properties satisfied by * on Q.
(ii) Define an operation * on Q as follows: a * b = (\(\frac { a+b }{ 2}\)); a, b ∈ Q. Examine the existence of identity and the existence of inverse for the operation * on Q.
Solution:

so, a * (b * c) ≠ (a * b) * c
Hence, the binary operation * is not associative.

(ii) a * b = (\(\frac { a+b }{ 2}\)); a, b ∈ Q
For identity, a * e = e * a = a
Now; a * e = a
\(\frac { a+e }{ 2}\) = a
a + e = 2a
e = 2a – a = a
Which is not possible
∴ Identity does not exist and hence the inverse does not exist.

Question 6.
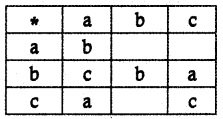
Fill in the following table so that the binary operation * on A = {a, b, c} is commutative.

Solution:
Given * is commutative on A = {a, b, c}

From the table, it is given that b * a = c
⇒ a * b = c
as * is commutative
c * a = a = a * c and
b * c = a = c * b

Question 7.
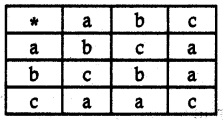
Consider the binary operation * defined on the set A = {a, b, c, d} by the following table:

Solution:
* is defined on the set A = {a, b, c, d} Given table

From the table a * b = c and b * a = d
⇒ a * b ≠ b * a
∴ * is not commutative.
Now(a * b) * c = c * c = a
a * (b * c) = a * b = c
⇒ (a * b) * c ≠ a * (b * c)
∴ * is not associative

Question 8.
Let

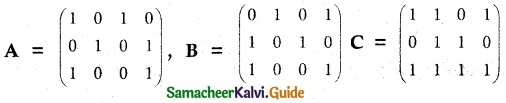
be any three boolean matrices of the same type. Find
(i) A v B
(ii) A ∧ B
(iii) (A v B) ∧ C
(iv) (A ∧ B) v C.
Solution:
Given boolean matrices

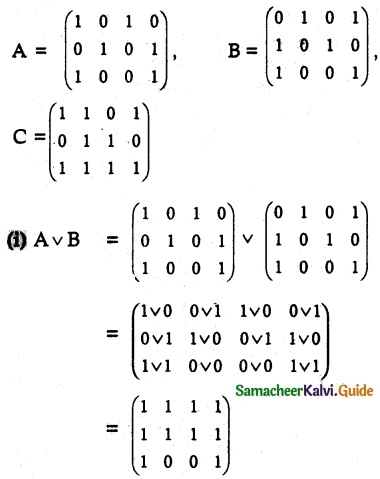
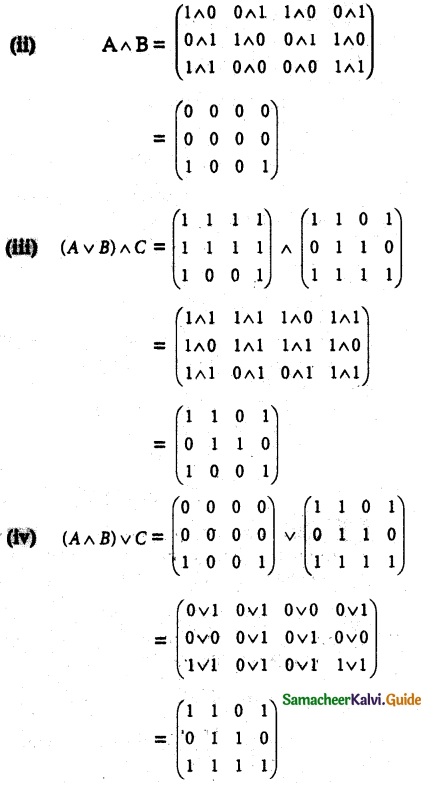
Question 9.
(i) Let M = \(\left\{\left(\begin{array}{ll}
x & x \\
x & x
\end{array}\right): x \in R-\{0\}\right\}\) and let * be the matrix multiplication. Determine whether M is closed under *. If so, examine the commutative and associative properties satisfied by * on M.
(ii) Let M = \(\left\{\left(\begin{array}{ll}
x & x \\
x & x
\end{array}\right): x \in R-\{0\}\right\}\) and let * be the matrix multiplication. Determine whether M is closed under *. If so, examine the existence of identity, existence of inverse properties for the operation * on M
Solution:

Since x ≠ 0, y ≠ 0, we see that 2xy ≠ 0 and so AB ∈ M. This shows that M is closed under matrix multiplication.
Commutative axiom:
AB = \(\left(\begin{array}{ll}
2xy & 2xy \\
2xy & 2xy
\end{array}\right)\)
= BA for all A, B ∈ M
Here, Matrix multiplication is commutative (though in general, matrix multiplication is not commutative)
Associative axiom:
Since matrix multiplication is associative, this axiom holds goods for M.

(ii) Identity axiom:

Also, we can show that EA = A
Hence E is the identity element in M

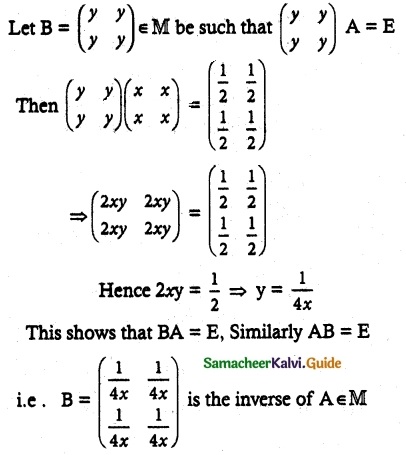
Question 10.
(i) Let A be Q\{1} Define * on A by x * y = x + y – xy. Is * binary on A ? If so, examine the commutative and associative properties satisfied by * on A.
(ii) Let A be Q\{1}. Define * on A by x * y = x + y – xy. Is * binary on A ? If so, examine the existence of an identity, the existence of inverse properties for the operation * on A.
Solution:
(i) Let a, b ∈ A (i.e.) a ≠ ±1 , b ≠ 1
Now a * b = a + b – ab
If a + b – ab = 1 ⇒ a + b – ab – 1 = 0
(i.e.) a(1 – b) – 1(1 – b) = 0
(a – 1)(1 – b) = 0 ⇒ a = 1, b = 1
But a ≠ 1 , b ≠ 1
So (a – 1) (1 – 6) ≠ 1
(i.e.) a * b ∈ A. So * is a binary on A.

To verify the commutative property:

Let a, b ∈ A (i.e.) a ≠ 1 , b ≠ 1
Now a * b = a + b – ab
and b * a = b + a – ba
So a * b = b * a ⇒ * is commutative on A.

To verify the associative property:
Let a, b, c ∈ A (i.e.) a, b, c ≠ 1
To prove the associative property we have to prove that
a * (b * c) = (a * b) * c

LHS: b * c = b + c – bc = D(say)
So a * (b * c) = a * D = a + D – aD
= a + (b + c – bc) – a(b + c – bc)
= a + b + c – bc – ab – ac + abc
= a + b + c – ab – bc – ac + abc …… (1)

RHS: (a * b) = a + b – ab = K(say)
So (a * b) * c = K * c = K + c – Kc
= (a + b – ab) + c – (a + b – ab) c
= a + b – ab + c – ac – bc + abc
= a + b + c – ab – bc – ac + abc ….. (2)

(ii) To verify the identity property:
Let a ∈ A (a ≠ 1)
If possible let e ∈ A such that
a * e = e * a = a
To find e:
a * e = a
(i.e.) a + e – ae = a

So, e = (≠ 1) ∈ A
(i.e.) Identity property is verified.
To verify the inverse property:
Let a ∈ A (i.e. a ≠ 1)
If possible let a’ ∈ A such that
To find a’:
a * a’ = e
(i.e.) a + a’ – aa’ = 0
⇒ a'(1 – a) = – a

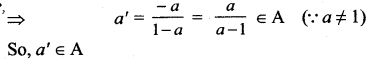
⇒ For every ∈ A there is an inverse a’ ∈ A such that
a* a’ = a’ * a = e
⇒ Inverse property is verified.