Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 12 Discrete Mathematics Ex 12.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.2
Question 1.
Let p : Jupiter is a planet and q: India is an island be any two simple statements. Give verbal sentence describing each of the following statements.
(i) ¬P
(ii) P ∧ ¬q
(iii) ¬p v q
(iv) p → ¬q
(v) p ↔ q
Solution:
p: Jupiter is a planet
q: India is an island
(i) ¬P : Jupiter is not a planet
(ii) P ∧ ¬q : Jupiter is a planet and India is not an island.
(iii) ¬p v q : Jupiter is not a planet or India is an island
(iv) p → ¬q : Jupiter is a planet then India is not an island
(v) p ↔ q : Jupiter is a planet if and only if India is an island
![]()
Question 2.
Write each of the following sentences in symbolic form using statement variables p and q.
(i) 19 is not a prime number and all the angles of a triangle are equal.
(ii) 19 is a prime number or all the angles of a triangle are not equal.
(iii) 19 is a prime number and all the angles of a triangle are equal.
(iv) 19 is not a prime number.
Solution:
Let p : 19 is a prime number
q : All the angles of a triangle are equal
(i) 19 is not a prime number and all the angles of a triangle are equal ⇒ ¬p ∧ q
(ii) 19 is a prime number or all the angles of a triangle are not equal ⇒ p v ¬q
(iii) 19 is a prime number and all the angles of a triangle are equal ⇒ p ∧ q
(iv) 19 is not a prime number ⇒ ¬p
Question 3.
Determine the truth value of each of the following statements
(i) If 6 + 2 = 5, then the milk is white.
(ii) China is in Europe dr √3 is art integer
(iii) It is not true that 5 + 5 = 9 or Earth is a planet.
(iv) 11 is a prime number and all the sides of a rectangle are equal.
Solution:
(i) If 6 + 2 = 5, then milk is white,
p: 6 + 2 = 5(F)
q: Milk is white (T)
∴ p → q is having the truth value T
(ii) China is in Europe or √3 is an integer
p: China is in Europe (F)
q: √3 is an integer (F)
∴ p v q is having the truth value F
(iii) It is not true that 5 + 5 = 9 or Earth is a planet
p: 5 + 5 = 9 (F)
q: Earth is a planet (T)
∴ ¬p v q is having the truth value T
(iv) 11 is a prime number and all the sides of a rectangle are equal.
p : 11 is a prime number (T)
q: All the sides of a rectangle are equal (F)
∴ p ∧ q is having the truth value F
![]()
Question 4.
Which one of the following sentences is a proposition?
- 4 + 7 = 12
- What are you doing?
- 3ⁿ ≤ 81, n ∈ N
- Peacock is our national bird.
- How tall this mountain is!
Solution:
- is a proposition
- not a proposition
- is a proposition
- is a proposition
- not a proposition
Question 5.
Write the converse, inverse, and contrapositive of each of the following implication.
(i) If x and y are numbers such that x = y, then x² = y²
(ii) If a quadrilateral is a square then it is a rectangle.
Solution:
(i) Converse: If x and y are numbers such that x2 = y2 then x = y.
Inverse: If x and y are numbers such that x ≠ y then x2 ≠ y2.
Contrapositive: If x and v are numbers such that x2 ≠ y2 then x ≠ y.
(ii) Converse: If a quadrilateral is a rectangle then it is a square.
Inverse: If a quadrilateral is not a square then it is not a rectangle.
Contrapositive: If a quadrilateral is not a rectangle then it is not a square.
![]()
Question 6.
Construct the truth table for the following statements.
(i) ¬P ∧ ¬q
(ii) ¬(P ∧ ¬q)
(iii) (p v q) v ¬q
(iv) (¬p → r) ∧ (p ↔ q)
Solution:
(i) ¬P ∧ ¬q
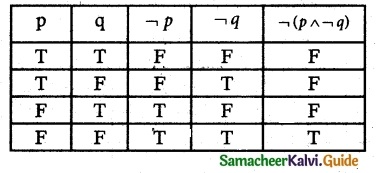
(ii) ¬(P ∧ ¬q)
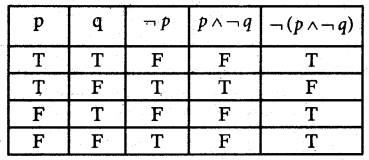
(iii) (p v q) v ¬q
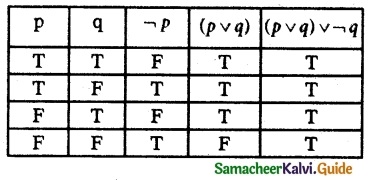
(iv) (¬p → r) ∧ (p ↔ q)
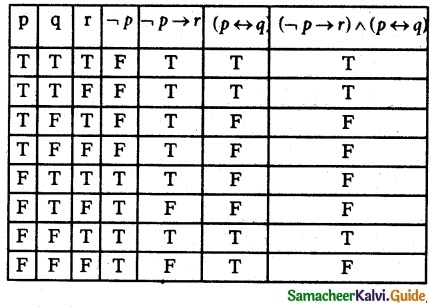
Question 7.
Verify whether the following compound propositions are tautologies or contradictions or contingency.
(i) (P ∧ q) ∧¬ (p v q)
(ii) ((P v q) ∧¬p) → q
(iii) (p → q) ↔ (¬p → q)
(iv) ((p → q) ∧ (q → r)) → (p → r)
Solution:
(i) (P ∧ q) ∧¬ (p v q)
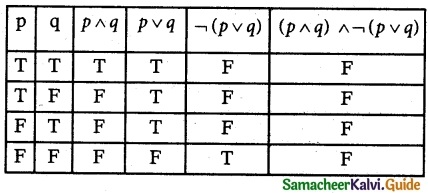
The entries in the last column are only F.
∴ The given statement is a contradiction
(ii) ((P v q) ∧¬p) → q
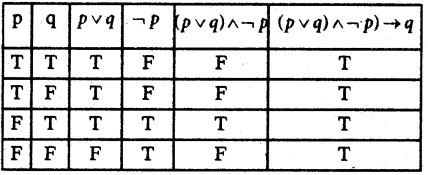
The entries in the last column are only T.
∴ The given statement is a Tautology
(iii) (p → q) ↔ (¬p → q)
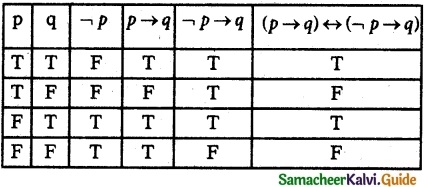
The entries in the last column are a combination of T and F.
∴ The given statement is a contingency.
(iv) ((p → q) ∧ (q → r)) → (p → r)
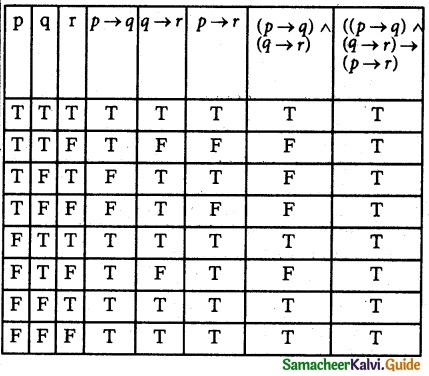
All the entries in the last column are only T.
∴ The given statement is a tautology.
![]()
Question 8.
Show that (i) ¬(p ∧ q) ≡ ¬P v ¬q
(ii) ¬(p → q) ≡ p ∧¬q
Solution:
(i) ¬(p ∧ q) ≡ ¬P v ¬q
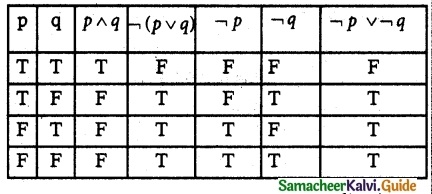
The entries in the columns corresponding to ¬(p ∧ q) and ¬P v ¬q are identical and hence they are equivalent.
(ii) ¬(p → q) ≡ p ∧ ¬q
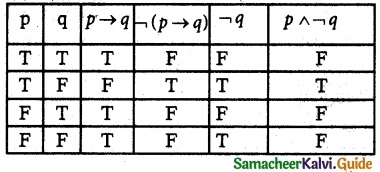
The entries in the columns corresponding to ¬(p → q) and p ∧ ¬q are identical and hence they are equivalent.
Question 9.
Prove that q → p ≡ ¬p → ¬q
Solution:
q → p ≡ ¬p → ¬q
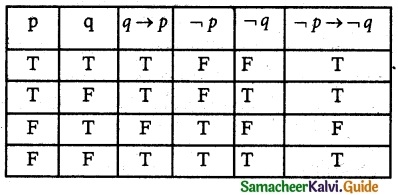
The entries in the columns corresponding to q → p and ¬p → ¬q are identical and hence they are equivalent.
∴ q → q = ¬p → ¬q
Hence proved.
![]()
Question 10.
Show that p → q and q → p are not equivalent
Solution:
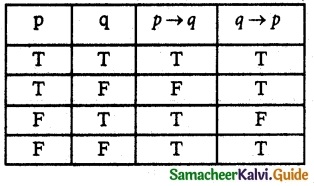
From the table, it is clear that
p → q ≠ q → P
Question 11.
Show that ¬(p ↔ q) ≡ p ↔ ¬q
Solution:
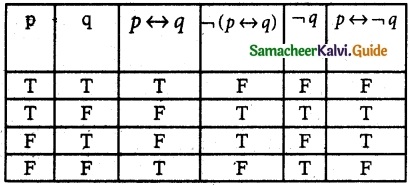
From the table, it is clear that
¬(p ↔ q) ≡ p ↔ ¬q
![]()
Question 12.
Check whether the statement p → (q → p) is a tautology or a contradiction without using the truth table.
Solution:
P → (q → p)
≡ P → (¬q v p) [∵ implication law]
≡ ¬p v (¬q v p) [∵ implication law]
≡ ¬p v (p v ¬q) [∵ Commutative law]
≡ (¬p V p) v (¬p v ¬q) [∵ Distribution law]
≡ T v ¬(p ∧ q) ≡ T [Tautology]
Hence p → (q → p) is a Tautology.
Question 13.
Using the truth table check whether the statements ¬(p v q) v (¬p ∧ q) and ¬P are logically equivalent.
Solution:
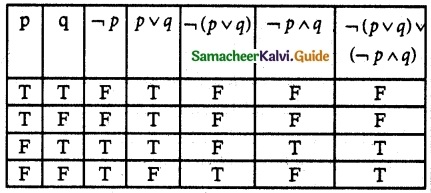
From the table, it is clear that ¬P and
¬(p v q) v (¬p ∧ q) are logically equivalent
i.e. ¬(p v q) v (¬p ∧ q) ≡ ¬p
Question 14.
Prove p → (q → r) ≡ (p ∧ q) → r without using the truth table.
Solution:
P → (q → r)
≡ P → (¬q v r) [∵ implication law]
≡ ¬p v (¬q v r) [∵ implication law]
≡ (¬p v ¬q) v r [∵ Associative law]
≡ ¬(p ∧ p) v r [∵ DeMorgan’s law]
≡ (p ∧ q) → r ≡ T [∵ implication law]
Hence Proved.
![]()
Question 15.
Prove that p → (¬q v r) ≡ ¬p v (¬q v r) using truth table.
Solution:
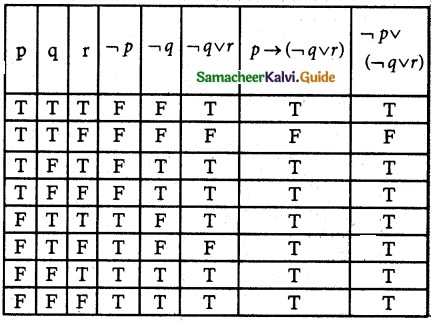
From the table, it is clear that the column of p → (¬q v r) and ¬p v (¬q v r) are identical.
∴ p → (¬q v r) ≡ ¬p v (¬q v r)
Hence proved.