Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.2 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.2
Question 1.
Evaluate the following if z = 5 – 2i and w = -1 + 3i
(i) z + w
Solution:
z = 5 – 2i, w = -1 + 3i
z + w = (5 – 2i) + (-1 + 3i)
= (5 – 1) + (-2i + 3i)
= 4 + i
(ii) z – iw
Solution:
z – iw = (5 – 2i) – i (-1 + 3i)
= 5 – 2i + i + 3
= (5 + 3) + (-2i + i)
= 8 – i
![]()
(iii) 2z + 3w
Solution:
2z + 3w = 2(5 – 2i) + 3 (-1 +3i)
= 10 – 4i – 3 + 9i
= 7 + 5 i
(iv) zw
Solution:
zw = (5 – 2i) (-1 + 3i)
= -5 + 15i + 2i – 6i2
= -5 + 17i + 6
= 1 + 17i
(v) z² + 2zw + w²
Solution:
= (z + w)2 [from (i)]
= (4 + i)2
= 16 – 1 + 8i
= 15 + 8i
![]()
(vi) (z + w)²
Solution:
(vi) (z + w)2 = 15 + 8z [from (v)]
Question 2.
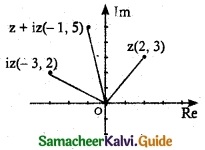
Given the complex number z = 2 + 3i, represent the complex numbers in the Argand diagram.
(i) z = 2 + 3i
iz = i(2 + 3i)
= (2i – 3)
= -3 + 2i
z + iz = (2 + 3i) + (-3 + 2i)
= -1 + 5i
![]()
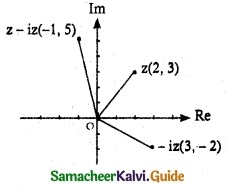
(ii) z, – iz and z – iz
z = 2 + 3i
-iz = -i (2 + 3i)
= -2i – 3i² = -2i + 3
= 3 – 2i
z- iz= 2 + 3i -3 + 2i
= 5 + i
![]()
Question 3.
Find the values of the real numbers x and y. if the complex numbers
(3 – i)x – (2 – i) y + 2i + 5 and 2x + (-1 + 2i)y + 3 + 2i are equal.
Solution:
(3 – i) x – (2 – i) y + 2i + 5 = 2x + (-1 + 2i) y + 3 + 2i
⇒ 3x – ix – 2y + iy + 2i + 5 = 2x – y + 2yi + 3 + 2i
⇒ (3x – 2y + 5) + 1 (-x + y + 2) = (2x – y + 3) + i (2y + 2)
Equate real parts on both sides
3x – 2y + 5 = 2x – y + 3
x – y = -2 ……. (1)
Equate imaginary parts on both sides
-x + y + 2 = 2y + 2
-x – y = 0
x + y = 0 ……. (2)
(1) + (2) ⇒ 2x = -2
x = -1
Substituting x = -1 in (2)
-1 + y = 0
⇒ y = 1
∴ x = -1, y = 1
![]()