Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.4 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.4
Question 1.
Write the following in the rectangular form:
(i) \(\overline { (5+9i)+(2-4i) } \)
Solution:
\(\overline { (5+9i)+(2-4i) } \)
= \(\overline {(5+9i)} \) + \(\overline {(2-4i)} \)
= 5 – 9i + 2 + 4i
= 7 – 5i
(ii) \(\frac {10-5i}{6+2i} \)
Solution:

(iii) \(\overline {3i} + \frac{2}{2-i}\)
Solution:
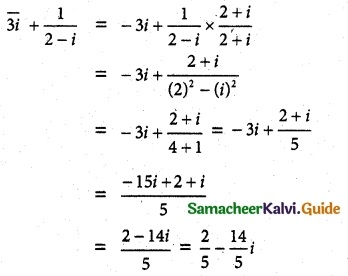
![]()
Question 2.
If z = x + iy, find the following in rectangular form.
(i) Re(\(\frac {1}{z} \))
Answer:
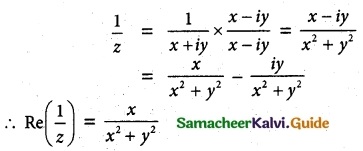
(ii) Re(i\(\bar{z}\)) = Re[i(\(\overline{x+i y}\))]
= Re(ix + y)
= y
(iii) Im(3z + 4\(\bar{z}\) – 4i)
= Im (3(x + iy) + 4(x – iy) – 4i)
= Im (3x + 3iy + 4x – 4iy – 4i)
= Im (3x + 4 + i (3y – 4y – 4)
= Im (3x + 4x + i(-y – 4))
= Im [7x + i(-y – 4)]
= -y – 4
= -(y + 4)
Question 3.
If z1 = 2 – i and z2 = -4 + 3i, find the inverse of z1, z2 and \(\frac {z_1}{z_2} \)
Solution:
z1 = 2 – i, z2 = -4 + 3i
z1 z2 = (2 – i) (-4 + 3i)
= -8 + 3 + 4i + 6i
= -5 + 10i
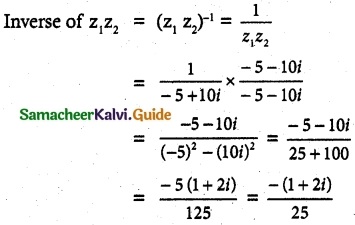
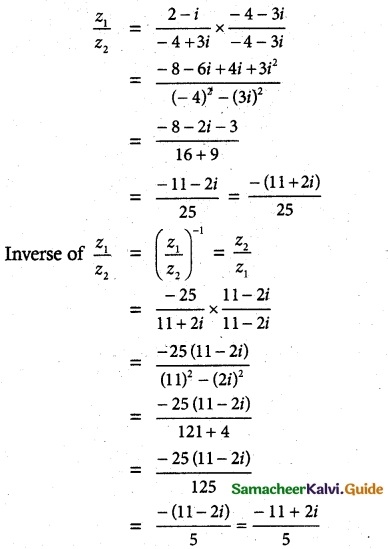
![]()
Question 4.
The complex numbers u, v, and w are related by \(\frac {1}{u}\) = \(\frac {1}{v}\) + \(\frac {1}{w}\). If v = 3 – 4i and w = 4 + 3i, find u in rectangular form.
Solution:
v = 3 – 4i, w = 4 + 3i
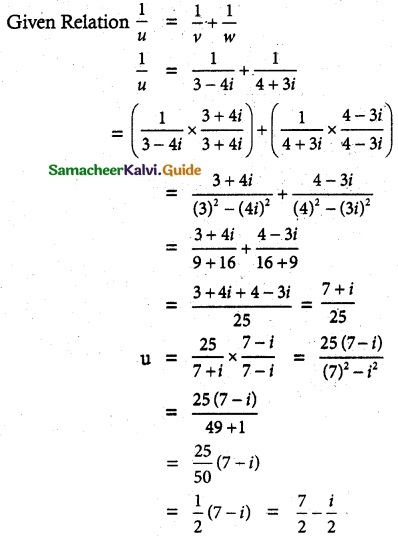
![]()
Question 5.
Prove the following properties:
(i) z is real if and only if z = \(\overline {z}\)
Solution:
z is real iff z = \(\bar{z}\)
Let z = x + iy
z = \(\bar{z}\)
⇒ x + iy = x – iy
⇒ 2iy = 0
⇒ y = 0
⇒ z is real.
z is real iff z = \(\bar{z}\)
(ii) Re(z) = \(\frac{z+\bar{z}}{2}\) and Im(z) = \(\frac{z-\bar{z}}{2i}\)
Solution:
let z = x + iy
\(\overline {z}\) = x – iy

Hence proved
![]()
Question 6.
Find the least value of the positive integer n for which (√3 + i)n (i) real, (ii) purely imaginary.
Solution:
Given (√3 + i)n
= (√3)² + 2i √3 + (i)²
= 3 + 2i √3 – 1
= 2 + 2i √3
= 2(1 + i√3)
put n = 3 or 4 or 5
then real part is not possible
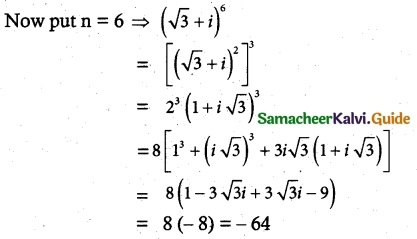
which is purely real ∴ n = 6
(ii) (√3 + i)n

which is purely imaginary
∴ n = 3
![]()
Question 7.
Show that
(i) (2 + i√3)10 – (2 – i√3)10 is purely imaginary.
Solution:
Let z = (2 + i√3)10 – (2 – i√3)10
Let Z

= (2 – i√3)10 – (2 + i√3)10
= -[(z + i√3)10 – (2 – i√3)10]
= -z
(2 + i√3)10 – (2 – i√3)10 is purely imaginary
![]()
(ii) \(\left(\frac{19-7 i}{9+i}\right)^{12}\) + \(\left(\frac{20-5 i}{7-6 i}\right)^{12}\) is real
Solution:

∴ z is real.