Samacheer Kalvi 12th Maths Guide Chapter 3 Theory of Equations Ex 3.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.3 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.3

Question 1.
Solve the cubic equation: 2x³ – x² – 18x + 9 = 0 if sum of two of its roots vanishes.
Solution:
The given equation is 2x³ – x² – 18x + 9 = 0
\(x^{3}-\frac{x^{2}}{2}-9 x+\frac{9}{2}=0\)
Let the roots be α, -α, β
α – α + β = \(-\left(\frac{-1}{2}\right)\)
\(\Rightarrow \beta=\frac{1}{2}\)
(α) (-α) (β) = \(\frac{-9}{2}\)
\(\Rightarrow-\alpha^{2}\left(\frac{1}{2}\right)=\frac{-9}{2}\)
α² = 9
α = ±3
The roots are 3, -3, \(\frac { 1 }{ 2 }\)

Question 2.
Solve the equation 9x³ – 36x² + 44x – 16 = 0 if the roots form an arithmetic progression.
Solution:
Given the roots are in AP
Let the roots be a – d, a, a + d

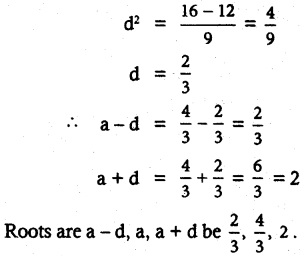
Question 3.
Solve the equation 3x³ – 26x² + 52x – 24 = 0 if its roots form a geometric progression.
Solution:

3 + 3λ + 3λ² = 13λ
3λ² + 3λ – 13λ + 3 = 0
3λ² – 10λ + 3 = 0
(λ – 3) (3λ – 1) = 0
λ = 6 or λ = \(\frac{1}{3}\)

Question 4.
Determine k and solve the equation 2x³ – 6x² + 3x + k = 0 if one of its roots is twice the sum of the other two roots.
Solution:
Given cubic equation
2x³ – 6x² + 3x + k = 0
Let the roots be α, β, γ
Given α = 2(β + γ)
β + γ = \(\frac{α}{2}\) ………. (1)
Sum of roots α(β + γ) = 3
From (1) α + \(\frac{α}{2}\) = 3
\(\frac{3α}{2}\) = 3 ⇒ α = 2
Again αβ + βγ + γα = \(\frac{3}{2}\)
α = 2 ⇒ 2β + βγ + 2γ = \(\frac{3}{2}\)
from (1) 2(\(\frac{α}{2}\)) + βγ = \(\frac{3}{2}\)
βγ = \(\frac{3}{2}\) – 2 = \(\frac{3-4}{2}\) = \(\frac{-1}{2}\)
βγ = \(\frac{-1}{2}\) ………… (2)
product of roots α β γ = –\(\frac{k}{2}\)
α = 2 ⇒ 2βγ = –\(\frac{k}{2}\)
βγ = –\(\frac{k}{4}\) ………… (3)

Question 5.
Find all zeros of the polynomial x⁶ – 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135, if it is known that 1 + 2i and √3 are two of its zeros.
Solution:
(i) Given that 1 + 2i, √3
Another roots be 1 – 2i, -√3
sum of roots = 1 + 2i + 1 – 2i
product roots = (1 + 2i)(1 – 2i)
1² + 2² = 1 + 4 = 5
x² – 2x + 5 = 0

(ii) sum of roots = √3 – √3
product roots = (√3)(-√3)
x² – 0x – 3 = 0
x² – 3 = 0
(x² – 2x + 5)(x² – 3) = x⁴ – 2x³ + 2x² + 6x – 15
x⁶– 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135
= (x⁴ – 2x³ + 2x² + 6x – 15)  (x² + px – 9)
Equate of co-efficient of x on both sides
-39 = -54 – 15 p
-39 + 54 = -15 p
15 = -15 p
p = -1
∴ x² – x – 9 = 0

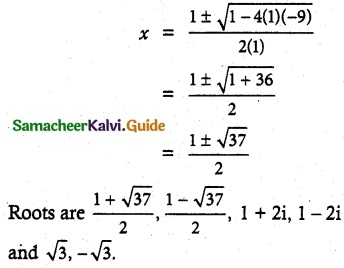
Question 6.
Solve the cubic equations:
(i) 2x³ – 9x² + 10x = 3,
2x³ – 9x² + 10x – 3 = 0
Solution:
(i) 2x³ – 9x² + 10x = 3
2x³ – 9x² + 10x – 3 = 0
sum of the coefficients 2 – 9 + 10 – 3 = 0
∴ x = 1 is one of the roots.

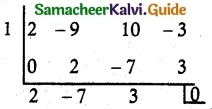
2x² – 7x + 3 = 0
(x – 3)(2x – 1) = 0
x = 3 or x = \(\frac{1}{2}\)
roots are 3, \(\frac{1}{2}\), 1

(ii) 8x³ – 2x² – 7x + 3 = 0
sum of the alternative coefficients are equal
8 – 7 = -2 + 3
1 = 1
∴ (x + 1) is a factor.

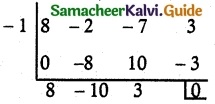
8x² – 10x + 3 = 0
(4x – 3) (2x – 1) = 0
4x  = 3 (or) 2x = 1
x = \(\frac{3}{4}\) (or) \(\frac{1}{2}\)
∴ The roots are \(\frac{3}{4}\), \(\frac{1}{2}\), -1

Question 7.
Solve the equation:
x⁴ – 14x² + 45 = 0
Solution:
Put t = x² ⇒ (x²)² – 14x² + 45 = 0
t² – 14t + 45 = 0
t² – 9t – 5t + 45 = 0
t(t – 9) – 5(t – 9) = 0
(t – 9)(t – 5) = 0
t – 9 = 0 or t – 5 = 0
t = 9 or t = 5
x² = 9 or x² = 5
x = ± 3 or y = ±√5
The roots are ±3, ±√5