Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.6 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.6
Question 1.
Discuss the maximum possible number of positive and negative roots of the polynomial equation 9x9 – 4x8 + 4x7 – 3x6 + 2x5 + x³ + 7x² + 7x + 2 = 0.
Solution:
P(x) = 9x9 – 4x8 + 4x7 – 3x6 + 2x5 + x3 + 7x2 + 7x + 2
The number of sign changes in P(x) is 4.
∴P(x) has at most 4 positive roots.
P(-x) = -9x9 – 4x8 – 4x7 – 3x6 – 2x5 – x3 + 7x2 – 7x + 2
The number of sign changes in P(-x) is 3.
P(x) has almost 3 negative roots.
Since the difference between the number of sign changes in co-efficient P(-x) and the number of negative roots of the polynomial P(x) is even.
The number of negative roots = at most 2.
![]()
Question 2.
Discuss the maximum possible number of positive and negative roots of the polynomial equations x² – 5x + 6 and x² – 5x + 16 . Also, draw a rough sketch of the graphs.
Solution:
y = x² – 5x + 6
x = 1, y = 1 – 5 + 6 = 2
x = 2, y = 4 – 10 + 6 = 0
x = 0, y = 6
x = 3, y = 9 – 15 + 6 = 0
x = -1, y = 1 + 5 + 6 = 12
x = 4, y = 16 – 20 + 6 = 2
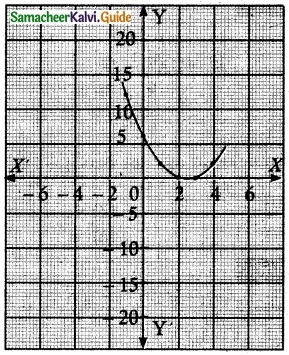
(1, 2), (0, 6), (-1, 12)
P(x) = (x² + 5x + 6) (x² – 5x + 16)
= x4 – 5x³ + 16x² – 5x³ + 25x² – 80x + 6x² – 30x + 96 = 0
= x4 – 10x³ + 47x² – 110x + 96 = 0
It has two sign changes
∴ It has two positive real roots
P(-x) = x4 + 10x³ + 47x² + 110x + 96
It has no sign change, no negative real roots
y = x2 – 5x + 16
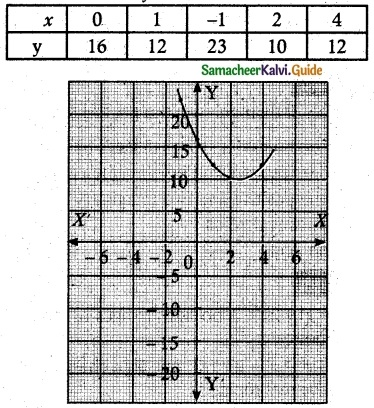
![]()
Question 3.
Show that the equation x9 – 5x5 + 4x4 + 2x² + 1 = 0 has atleast 6 imaginary solutions.
Solution:P(x) = x9 – 5x5 + 4x4 + 2x2 + 1
(i) The number of sign changes in P(x) is 2. The number of positive roots is atmost 2.
(ii) P(-x) = -x9 + 5x5 + 4x4 + 2x2 + 1. The number of sign changes in P(-x) is 1. The number of negative roots of P (x) is atmost 1. Since the difference of number of sign changes in P(-x) and number of negative zeros is even.
P(x) has one negative root.
(iii) 0 is not the zero of the polynomial P(x). So the number of real roots is almost 3.
∴ The number of imaginary roots at least 6.
![]()
Question 4.
Determine the number of positive and negative roots of the equation x9 – 5x8 – 14x7 = 0.
Solution:
P(x) = x9 – 5x8 – 14x7. It has only one sign change.
∴ It has one positive roots.
P(-x) = -x9 – 5x8 + 14x7. It has only one sign change.
It has one negative root.
∴ It has one positive and one negative roots.
![]()
Question 5.
Find the exact number of real roots and imaginary of the equation x9 + 9x7 + 7x5 + 5x³ + 3x.
Solution:
P(x) = x9 + 9x7 + 7x5 + 5x3 + 3x.
There is no change in the sign of P(x) and P(-x), P(x) has no positive and no negative real roots, but 0 is the root of the polynomial equation P(x).
![]()