Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 Inverse Trigonometric Functions Ex 4.1 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1
Question 1.
Find all the values of x such that
Solution:
(i) sin x = 0
⇒ x = nπ
where n = 0, ±1, ±2, ±3, ……., ±10
(ii) sin x = -1
⇒ x = (4n – 1) \(\frac{\pi}{2}\), n = 0, ±1, ±2, ±3, 4
Question 2.
Find the period and amplitude of
Solution:
(i) y = sin 7x
For Amplitude use the form
y = a sin(bx – c) + d
Amplitude = |a|
a = 1, ∴ |a| = 1
Period using the formula = \(\frac{2π}{|b|}\) = \(\frac{2π}{|7|}\) = \(\frac{2π}{7}\)
∴ Amplitude = 1
Period = \(\frac{2π}{7}\)
(ii) y = -sin (\(\frac{1}{3}\)x)
a = -1, b = \(\frac{1}{3}\)
∴ Amplitude = |a| = |-1| = 1
Period = \(\frac{2π}{|b|}\) = \(\frac{2π}{| \frac{1}{3}|}\) = 3(2π) = 6π
(iii) y =4 sin (-2x)
a = 4, b = -2
Amplitude = |4| = 4
Period = \(\frac{2π}{|b|}\) = \(\frac{2π}{|-2|}\) = \(\frac{2π}{2}\) = π
![]()
Question 3.
Sketch the graph of y = sin (\(\frac{1}{3}\)x) for 0 ≤ x ≤ 6π
Solution:
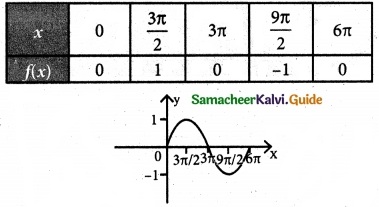
![]()
Question 4.
Find the value of
(i) sin-1 (sin(\(\frac{2π}{3}\)))
(ii) sin-1 (sin(\(\frac{5π}{4}\)))
Solution:
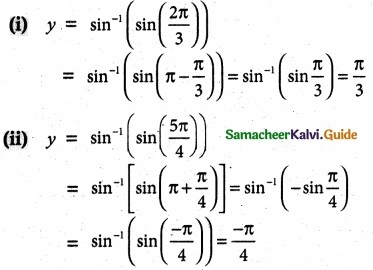
![]()
Question 5.
For what value of x does sin x = sin-1 x?
Solution:
sin x = sin-1 x is possible only when x = 0 (∵ x ∈ R)
Question 6.
Find the domain of the following
(i) f(x) = sin-1 (\(\frac{x²+1}{2x}\))
Solution:
f(x) = sin-1 (\(\frac{x²+1}{2x}\))
Range of sin-1x is [-1, 1]
-1 ≤ \(\frac{x²+1}{2x}\) ≤ 1
Multiply by 2x² ≥ 0

∴ solution is [-1, 1]
![]()
(ii) g (x) = 2 sin-1 (2x – 1) – \(\frac{π}{4}\)
Range of 2 sin-1 x is [-1, 1]
-1 ≤ 2x – 1 ≤ 1
2x – 1 ≤ 1 (or) 2x – 1 ≥ -1
2x ≤ 2 (or) 2x ≥ -1 + 1
x ≤ 1 (or) 2x ≥ 0 ⇒ x ≥ 0
x ≥ 0 and x ≤ 1
∴ solution is [0, 1]
Question 7.
Find the value of
(sin\(\frac{5π}{9}\) cos\(\frac{π}{9}\) + cos\(\frac{5π}{9}\) sin\(\frac{π}{9}\))
Solution:
sin (A + B) = sin A cos B + cos A sin B

![]()