Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 Inverse Trigonometric Functions Ex 4.6 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.6
Choose the most suitable answer from the given four alternatives:
Question 1.
The value of sin-1(cos x), 0 ≤ x ≤ π is
(a) π – x
(b) x – \(\frac {π}{2}\)
(c) \(\frac {π}{2}\) – x
(d) x – π
Solution:
(c) \(\frac {π}{2}\) – x
Hint:
sin-1(cos x) = sin-1(sin(\(\frac {π}{2}\) – x)) = \(\frac {π}{2}\) – x
Question 2.
If sin-1 x + sin-1 y = \(\frac {2π}{3}\); then cos-1 x + cos-1 y is equal to
(a) \(\frac {2π}{3}\)
(b) \(\frac {π}{3}\)
(c) \(\frac {π}{6}\)
(d) π
Solution:
(b) \(\frac {π}{3}\)
Hint:
sin-1x + cos-1x + cos-1y + sin-1y = \(\frac {π}{2}\) + \(\frac {π}{2}\) = π
\(\frac {2π}{3}\) + cos-1x + cos-1y = π
cos-1x + cos-1y = π – \(\frac {2π}{3}\) = \(\frac {3π-2π}{3}\) = \(\frac {π}{3}\)
![]()
Question 3.
sin-1\(\frac {3}{5}\) – cos-1\(\frac {12}{13}\) + sec-1\(\frac {5}{3}\) – cosec-1\(\frac {13}{12}\) is equal to
(a) 2π
(b) π
(c) 0
(d) tan-1\(\frac {12}{65}\)
Solution:
(c) 0
Hint:

Question 4.
If sin-1 x = 2sin-1 α has a solution, then
(a) |α| ≤ \(\frac {1}{√2}\)
(b) |α| ≥ \(\frac {1}{√2}\)
(c) |α| < \(\frac {1}{√2}\)
(d) |α| > \(\frac {1}{√2}\)
Solution:
(a) |α| ≤ \(\frac {1}{√2}\)
Hint:
If sin-1 x = 2sin-1 α has a solution then
–\(\frac {π}{2}\) ≤ 2sin-1α ≤ \(\frac {π}{2}\)
–\(\frac {π}{4}\) ≤ sin-1α ≤ \(\frac {π}{4}\)
sin(\(\frac {-π}{4}\)) ≤ α ≤ sin\(\frac {π}{4}\)
–\(\frac {1}{√2}\) ≤ α ≤ \(\frac {1}{√2}\)
-|α| ≤ \(\frac {1}{√2}\)
![]()
Question 5.
sin-1(cos x) = \(\frac {π}{2}\) – x is valid for
(a) -π ≤ x ≤ 0
(b) 0 ≤ x ≤ π
(c) –\(\frac {π}{2}\) ≤ x ≤ \(\frac {π}{2}\)
(d) –\(\frac {π}{4}\) ≤ x ≤ \(\frac {3π}{4}\)
Solution:
(b) 0 ≤ x ≤ π
Hint:
sin-1 (cosx) = \(\frac {π}{2}\) – x is valid for
cos x = sin (\(\frac {π}{2}\) – x)
cos x ∈ [0, π]
∴ 0 ≤ x ≤ π
Question 6.
If sin-1 x + sin-1 y + sin-1 z = \(\frac {3π}{2}\), the value of show that x2017 + y2018 + z2019 – \(\frac {9}{x^{101}+y^{101}+z^{101}}\) is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0
Hint:
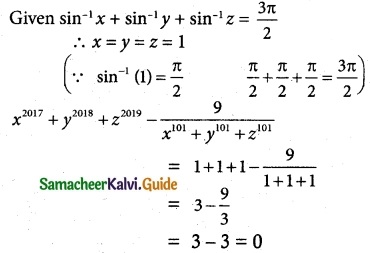
![]()
Question 7.
If cot-1 x = \(\frac {2π}{5}\) for some x ∈ R, the value of tan-1 x is
(a) –\(\frac {π}{10}\)
(b) \(\frac {π}{5}\)
(c) \(\frac {π}{10}\)
(d) –\(\frac {π}{5}\)
Solution:
(c) \(\frac {π}{10}\)
Hint:
tan-1 x + cos-1 \(\frac {π}{2}\)
tan-1x = \(\frac {π}{2}\) – cot-1 x = \(\frac {π}{2}\) – \(\frac {2π}{5}\)
= \(\frac {5π-4π}{10}\) = \(\frac {π}{10}\)
Question 8.
The domain of the function defined by f(x) = sin-1 \(\sqrt {x-1}\) is
(a) [1, 2]
(b) [-1, 1]
(c) [0, 1]
(d) [-1, 0]
Solution:
(a) [1, 2]
Hint:
f(x) = sin-1 \(\sqrt {x-1}\)
\(\sqrt {x-1}\) ≥ 0
-1 ≤ \(\sqrt {x-1}\) ≤ 1
∴ 0 ≤ \(\sqrt {x-1}\) ≤ 1
0 ≤ x – 1 ≤ 1
1 ≤ x ≤ 2
x ∈ [1, 2]
![]()
Question 9.
If x = \(\frac {1}{5}\) the value of cos(cos-1x + 2sin-1x) is
(a) –\(\sqrt{\frac {24}{25}}\)
(b) \(\sqrt{\frac {24}{25}}\)
(c) \(\frac {1}{5}\)
(d) –\(\frac {1}{5}\)
Solution:
(d) –\(\frac {1}{5}\)
Hint:
cos[cos-1x + sin-1x + sin-1x] = cos(\(\frac {π}{2}\) + sin-1x)
= -sin(sin-1x)
[∵ cos(90+θ) = -sin θ]
= -x = –\(\frac {1}{5}\)
Question 10.
tan-1(\(\frac {1}{4}\)) + tan-1(\(\frac {2}{9}\)) is equal to
(a) \(\frac {1}{2}\)cos-1(\(\frac {3}{5}\))
(b) \(\frac {1}{2}\)sins-1(\(\frac {3}{5}\))
(c) \(\frac {1}{2}\)tan-1(\(\frac {3}{5}\))
(d) tan-1(\(\frac {1}{2}\))
Solution:
(d) tan-1(\(\frac {1}{2}\))
Hint:

![]()
Question 11.
If the function f(x) = sin-1(x² – 3), then x belongs to
(a) [-1, 1]
(b) [√2, 2]
(c) [-2, -√2]∪[√2, 2]
(d) [-2, -√2]
Solution:
(c) [-2, -√2]∪[√2, 2]
Hint:
-1 ≤ x² – 3 ≤ 1
-1 + 3 ≤ x² ≤ 1 + 3
⇒ 2 ≤ x² ≤ 4
±√2 ≤ x ≤ ± 2
[-2, -√2]∪[√2, 2]
Question 12.
If cot-1 2 and cot-1 3 are two angles of a triangle, then the third angle is
(a) \(\frac {π}{4}\)
(b) \(\frac {3π}{4}\)
(c) \(\frac {π}{6}\)
(d) \(\frac {π}{3}\)
Solution:
(b) \(\frac {3π}{4}\)
Hint:
A + B + C = π (triangle)
cot-1 2 + cot-1 3 + C = π

![]()
Question 13.
sin-1(tan\(\frac {π}{4}\)) – sin-1(\(\sqrt{\frac {3}{x}}\)) = \(\frac {π}{6}\). Then x is root of the equation
(a) x² – x – 6 = 0
(b) x² – x – 12 = 0
(c) x² + x – 12 = 0
(d) x² + x – 6 = 0
Solution:
(b) x² – x – 12 = 0
Hint:

Question 14.
sin-1(2 cos²x – 1) + cos-1(1 – 2 sin²x) =
(a) \(\frac {π}{2}\)
(b) \(\frac {π}{3}\)
(c) \(\frac {π}{4}\)
(d) \(\frac {π}{6}\)
Solution:
(a) \(\frac {π}{2}\)
Hint:
sin-1(2 cos² x – 1) + cos-1(1 – 2 sin²x)
= sin-1 (2 cos² x – 1) + cos-1 (1 – sin² x – sin² x)
= sin-1(2 cos² x – 1) + cos-1(cos² x – (1 – cos²x))
= sin-1(2 cos² x – 1) + cos-1(cos² x – 1 + cos²x)
= sin-1(2 cos² x – 1) + cos-1(2 cos² x – 1)
= \(\frac {π}{2}\) [∵ sin-1 x + cos-1 x = \(\frac {π}{2}\)]
![]()
Question 15.
If cot-1(\(\sqrt {sinα}\)) + tan-1(\(\sqrt {sinα}\)) = u, then cos 2u is equal to
(a) tan²α
(b) 0
(c) -1
(d) tan 2α
Solution:
(c) -1
Hint:
cot-1 x + tan-1 x = \(\frac {π}{2}\)
∴ u = \(\frac {π}{2}\)
cos 2u = cos 2(\(\frac {π}{2}\)) = cos π = -1
Question 16.
If |x| ≤ 1, then 2 tan-1 x – sin-1\(\frac {2x}{1+x²}\) is equal to
(a) tan-1x
(b) sin-1x
(c) 0
(d) π
Solution:
(c) 0
Hint:
sin-1\(\frac {2x}{1+x²}\) = 2 tan-1x
∴ 2 tan-1 x – 2 tan-1 x = 0
![]()
Question 17.
The equation tan-1 x – cot-1 x = tan-1(\(\frac {1}{√3}\)) has
(a) no solution
(b) unique solution
(c) two solutions
(d) infinite number of solutions
Solution:
(b) unique solution
Hint:
tan-1 x – cot-1 x = tan-1(\(\frac {1}{√3}\)) …….. (1)
tan-1 x – cot-1 x = \(\frac {π}{2}\) ……… (2)
Add 1 and 2
2 tan-1 x = \(\frac {π}{6}\) + \(\frac {π}{2}\) = \(\frac {2π}{3}\)
tan-1 x = \(\frac {π}{3}\)
x = √3 which is uniqe solution.
Question 18.
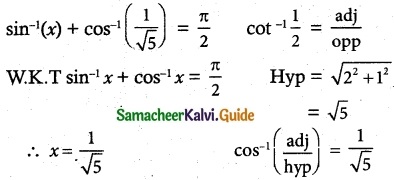
If sin-1 x + cot-1(\(\frac {1}{2}\)) = \(\frac {π}{2}\), then x is equal to
(a) \(\frac {1}{2}\)
(b) \(\frac {1}{√5}\)
(c) \(\frac {2}{√5}\)
(d) \(\frac {√3}{2}\)
Solution:
(b) \(\frac {1}{√5}\)
Hint:
![]()
Question 19.
If sin-1 \(\frac {x}{5}\) + cosec-1\(\frac {5}{4}\) = \(\frac {π}{2}\), then the value of x is
(a) 4
(b) 5
(c) 2
(d) 3
Solution:
(d) 3
Hint:

Question 20.
sin(tan-1 x), |x| < 1 is equal to
(a) \(\frac {x}{\sqrt{1-x^2}}\)
(b) \(\frac {1}{\sqrt{1-x^2}}\)
(c) \(\frac {1}{\sqrt{1+x^2}}\)
(d) \(\frac {x}{\sqrt{1+x^2}}\)
Solution:
(d) \(\frac {x}{\sqrt{1+x^2}}\)
Hint:
tan a = x
W.K.T 1 + tan² a = sec² a
1 + x² = sec² a
sec a = \(\sqrt{1+x^2}\)
\(\frac {1}{cosa}\) = \(\sqrt{1+x^2}\)
cos a= \(\frac {1}{\sqrt{1+x^2}}\)
sin a = \(\sqrt{1-cos^2a}\) = \(\sqrt{1-\frac {1}{1+x^2}}\)
\(\sqrt{\frac{1+x^2 -1}{1+x^2}}\) = \(\frac {x}{\sqrt{1+x^2}}\)
![]()