Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1
Question 1.
Obtain the equation of the circles with a radius of 5 cm and touching the x-axis at the origin in a general form.
Solution:
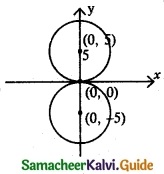
Given radius = 5 cm and the circle is touching x axis
So centre will be (0, ± 5) and radius = 5
The equation of the circle with centre (0, ± 5) and radius 5 units is
(x – 0)2 + (y ± 5)2 = 52
(i.e) x2 + y2 ± 10 y + 25 – 25 = 0
(i.e) x2 + y2 ± 10y = 0
![]()
Question 2.
Find the equation of the circle with centre (2, – 1) and passing through the point (3, 6) in standard form.
Solution:
Centre = (2, -1) = (h, k)
Passing through the point (3, 6)
Equation of the circle (x – h)² + (y – k)² = r² ………. (1)
(3 – 2)² + (6 + 1)² = r²
1² + 7² = r²
1 + 49 = r²
r² = 50
(1) ⇒ (x – 2)² + (y + 1)² = 50
Question 3.
Find the equation of circles that touch both the axes and pass-through (-4, -2) in a general form.
Solution:
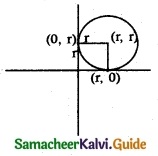
Since the circle touches both the axes, its centre will be (r, r) and the radius will be r.
Here centre = C = (r, r) and point on the circle is A = (-4, -2)
CA = r ⇒ CA2 = r2
(i.e) (r + 4)2 + (r + 2)2 = r2
⇒ r2 + 8r +16 + r2 + 4r + 4 – r2 = 0
(i.e) r2 + 12r + 20 = 0
(r + 2) (r + 10) = 0
⇒ r = -2 or -10
When r = -2, the equation of the circle will be (x + 2)2 + (y + 2)2 = 22
(i.e) x2 + y2 + 4x + 4y + 4 = 0
When r = -10, the equation of the circle will be (x + 10)2 + (y + 10)2 = 102
(i.e) x2 + y2 + 20x + 20y + 100 = 0
![]()
Question 4.
Find the equation of the circles with centre (2, 3) and passing through the intersection of the lines 3x – 2y – 1 =0 and 4x + y – 27 = 0.
Solution:
centre (2, 3) = (h, k)
Point of intersection
Solve 3x – 2y – 1 = 0 ………. (1)
4x + y – 27 = 0 ……… (2)
(1) ⇒ 3x – 2y = 1
(2) × 2 ⇒ 8x + 2y = 54
11x = 55
x = 5
put in (1)
15 – 2y – 1 = 0
14 = 2y
y = 7
Passing-through point is (5, 7)
Equation of circle be (x – h)² + (y – k)² = r² ……….(3)
(5 – 2)² + (7 – 3)² = r²
3² + 4² = r²
r² = 25
∴ (3) ⇒ (x – 2)² + (y – 3)² = 25
x² – 4x + 4 + y² – 6y + 9 – 25 = 0
x² + y² – 4x – 6y – 12 = 0
Question 5.
Obtain the equation of the circle for which (3, 4) and (2, -7) are the ends of a diameter.
Solution:
The equation of a circle with (x1 , y1) and (x2 , y2 ) as end points of a diameter is
(x – x1 )(x – x2) + (y – y1 )(y – y2) = 0
Here the end points of a diameter are (3, 4) and (2, -7)
So equation of the circle is (x – 3 )(x – 2 ) + (y – 4) (y + 7.) = 0
x2 + y2 – 5x + 37 – 22 = 0
![]()
Question 6.
Find the equation of the circle through the points (1, 0), (-1, 0) and (0, 1).
Solution:
Let the general equation of the circle be
x² + y² + 2gx + 2fy + c = 0
It passes through the points (1, 0), (-1, 0) and (0,1)
1 + 0 + 2g + c = 0
2g + c = -1 ………(1)
1 + 0 – 2g + c = 0
-2g + c = -1 …………(2)
0 + 1 + 0 + 2f + c = 0
2f + c = -1
(1) + (2) ⇒ 2c = -2
c = -1
substitute in eqn (1)
2g – 1 = -1
2g = 0
g = 0
substitute in eqn (3)
2f – 1 = -1
2f = -1 + 1
2f = 0
f = 0
Therefore, the required equation of the circle
x² + y² – 1 = 0
Question 7.
A circle of area 9π square units has two of its diameters along the lines x + y = 5 and: x – y = 1. Find the equation of the circle.
Solution:

Area of the circle = 9π
(i.e) πr2 = 9π
⇒ r2 = 9 ⇒ r = 3
(i.e) radius of the circle = r = 3
The two diameters are x + y = 5 and x – y = 1
The point of intersection of the diameter is the centre of the circle = C
To find C: Solving x + y = 5 ……… (1)
x – y = 1 ………. (2)
(1) + (2) ⇒ 2x = 6 ⇒ x = 3
Substituting x = 3 in (1) we get
3 + y = 5 ⇒ y = 5 – 3 = 2
∴ Centre = (3, 2) and radius = 3
So equation of the circle is (x – 3)2 + (y – 2)2 = 32
(i.e) x2 + y2 – 6x – 4y + 4 = 0
![]()
Question 8.
If y = 2√2 x + c is a tangent to the circle x² + y² = 16, find the value of c.
Solution:
The condition of the line y = mx + c to be a tangent to the circle x² + y² = a² is
c² = a²( 1 + m²)
a² = 16; m = 2√2 ⇒ m² = 4 × 2 = 8
c² = 16(1+8)
c² = 16(9)
c = ±4 × 3 = ±12
∴ c = ± 12.
Question 9.
Find the equation of the tangent and normal to the circle x² + y² – 6x + 6y – 8 = 0 at (2, 2).
Solution:
The equation of the tangent to the circle x2 + y2 + 2 gx + 2fy + c = 0 at (x1, y1) is
xx1 + yy1 + g(x + x1) + f(y + y1) + c = 9
So the equation of the tangent to the circle
x2 + y2 – 6x + 6y – 8 = 0 at (x1, y1) is
xx1 + yy1 – \(\frac{6\left(x+x_{1}\right)}{2}+\frac{6\left(y+y_{1}\right)}{2}\) – 8 = 0
(i.e) xx1 + yy1 – 3(x + x1) + 3(y + y1) – 8 = 0
Here (x1, y1) = (2, 2)
So equation of the tangent is
x(2) + y(2) – 3(x + 2) + 3(y + 2) – 8 = 0
(.i.e) 2x + 2y – 3x – 6 + 3y + 6 – 8 = 0
(i.e) -x + 5y – 8 = 0 or x – 5y + 8=0
Normal is a line ⊥r to the tangent
So equation of normal circle be of the form 5x + y + k = 0
The normal is drawn at (2, 2)
⇒ 10 + 2 + k = 0 ⇒ k = -12
So equation of normal is 5x + y – 12 = 0
![]()
Question 10.
Determine whether the points (- 2, 1), (0, 0) and s (- 4, – 3) lie outside, on or inside the circle x² + y² – 5x + 2y – 5 = 0.
Solution:
x² + y² – 5x + 2y – 5 = 0
(i) At (-2, 1) ⇒ (-2)² + 1² – 5(-2) + 2(1) – 5
= 4 + 1 + 10 + 2 – 5 = 12 > 0
∴ (-2, 1) lies outside the circle.
(ii) At(0, 0) ⇒ 0 + 0 – 0 + 0 – 5 = -5 < 0
(0, 0) lies inside the circle.
(iii) At (-4, -3) ⇒ (-4)² + (- 3)² – 5(-4) + 2(-3) – 5 = 16 + 9 + 20 – 6 – 5 = 34 > 0
(-4, -3) lies outside the circle.
Question 11.
Find the centre and radius of the following circles.
(i) x² + (y + 2)² = 0
(ii) x² + y² + 6x – 4y + 4 = 0
(iii) x² + y² – x + 2y – 3 = 0
(iv) 2x² + 2y² – 6x + 4y + 2 = 0
Solution:
(i) x2 + (y + 2)2 = 0
(i.e) x2 + y2 + 4y + 4 = 0
Comparing this equation with the general form x2 + y2 + 2gx + 2fy + c = 0
we get 2g = 0 ⇒ g = 0
2f = 4 ⇒ f= 2 and c = 4
Now centre = (-g, -f) = (0, -2)
Radius = r = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{0+4-4}\)
∴ Centre = (0, -2) and radius = 0
(ii) x2 + y2 + 6x – 4y + 4 = 0
Comparing with the general form we get
2g = 6, 2f = -4
⇒ g = 3, /= -2 and c = 4
Centre = (-g, -f) = (-3, 2)
Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{9+4-4}\)= 3
∴ Centre = (-3, 2) and radius = 3
(iii) x² + y² – x + 2y – 3 = 0
2g = -1; 2f = 2; c = -3
g = \(\frac{-1}{2}\) f = 1
Centre (-g, -f) = (\(\frac{1}{2}\), -1)
Radius = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{\frac{1}{4}+1+3}\)
\(\sqrt{\frac{1+4+12}{4}}\)
\(\sqrt{\frac{17}{4}}\) = \(\frac{\sqrt{17}}{2}\)
(iv) 2x2 + 2y2 – 6x + 4y + 2 = 0
(÷ by 2) ⇒ x2 + y2 – 3x + 2y + 1 =0
Comparing this equation with the general form of the circle we get
2g = -3, 2f= 2
g = \(-\frac{3}{2}\), g= 1 and c = 1
So centre = (-g, -f) = (\(\frac{3}{2}\), -1)
and radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{\frac{9}{4}+1-1}=\frac{3}{2}\)
∴ Centre = (\(\frac{3}{2}\), -1) and radius = \(\frac{3}{2}\)
![]()
Question 12.
If the equation 3x² + (3 – p) xy + qy² – 2px = 8pq represents a circle, find p and q. Also determine the centre and radius of the circle.
Solution:
3x² + (3 – p) xy + qy² – 2px = 8pq represent a circle means,
Co-efficient of x² = co-efficient of y²
3 = q ⇒ q = 3
Co-efficient of xy = 0
3 – p = 0 ⇒ p = 3
3x² + 3y² – 6x = 8 (3)(3)
3x² + 3y² – 6x – 72 = 0
(÷3) x² + y² – 2x – 24 = 0
2g = -2; 2f = 0; c = -24
g = -1 f = 0
Centre (-g, -f) = (1, 0)
Radius = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{1+0+24}\)
= \(\sqrt{25}\) = 5
![]()