Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.6 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.6
Choose the most suitable answer from the given four alternatives:
Question 1.
The equation of the circle passing through (1, 5) and (4, 1) and touching y-axis is x² + y² – 5x – 6y + 9 + λ (4x + 3y – 19) = 0 where λ is equal to
(a) 0, –\(\frac {40}{9}\)
(b) 0
(c) \(\frac {40}{9}\)
(d) –\(\frac {40}{9}\)
Solution:
(a) 0, –\(\frac {40}{9}\)
Hint:
x² + y² – 5x – 6y + 9 + λ(4x + 3y – 19) = 0
x² + y² + x (-5 + 4λ) + y (- 6 + 3λ) + 9 – 19λ = 0
It touches the y-axis put x = 0.
y² + (3λ – 6) y + 9 – 19λ = 0
Now, b² – 4ac = 0
⇒ (3λ – 6)² – 4 (1) (9 – 19λ) = 0
Solving this equation we get
λ = 0 or λ = –\(\frac {40}{9}\)
![]()
Question 2.
The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half the distence between the foci is
(a) \(\frac {4}{3}\)
(b) \(\frac {4}{√3}\)
(c) \(\frac {2}{√3}\)
(d) –\(\frac {3}{2}\)
Solution:
(c) \(\frac {2}{√3}\)
Hint:
Length of Latus Rectum \(\frac {2b^2}{a}\) = 8
⇒ b² = 4a …….. (1)
Length of conjugate axes
2b = \(\frac {1}{2}\)(2ae)
⇒ b = \(\frac {1}{2}\) …….. (2)
b² = \(\frac {a^2e^2}{4}\)
Now b² = a²(e² – 1)
\(\frac {a^2e^2}{4}\) = a²(e² – 1)
e² = 4e² – 4
3e² = 4
e² = \(\frac {4}{3}\)
∴ e = \(\frac {2}{√3}\)
Question 3.
The circle x² + y² = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if
(a) 15 < m < 65
(b) 35 < m < 85
(c) -85 < m < -35
(d) -35 < m < 15
Solution:
(d) -35 < m < 15
Hint:
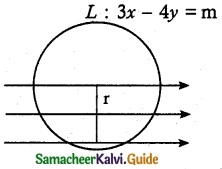
C : x² + y² – 4x – 8y – 5 = 0
(x – 2)² + (y – 4)² = 25
C (2, 4); r = 5
Distance from centre < r
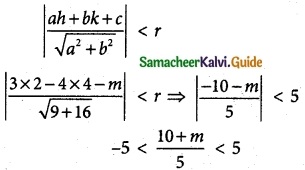
-25 < 10 + m < 25
⇒ -25 – 10 < m < 25 – 10
-35 < m < 15
![]()
Question 4.
The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3).
(a) \(\frac {6}{5}\)
(b) \(\frac {5}{3}\)
(c) \(\frac {10}{3}\)
(d) \(\frac {3}{5}\)
Solution:
(c) \(\frac {10}{3}\)
Hint:
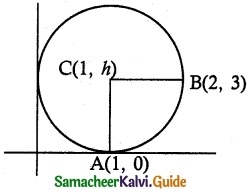
CA = CB
CA² = CB²
(1 – 1)² + (h – 0)² = (1 – 2)² + (h – 3)²
h² = 1 + h² + 9 – 6h
6h = 10
h = \(\frac {10}{6}\) = \(\frac {5}{3}\)
Diameter is 2h = 2(\(\frac {5}{3}\)) = \(\frac {10}{3}\)
Question 5.
The radius of the circle 3x² + by² + 4bx – 6by + b² = 0 is
(a) 1
(b) 3
(c) \(\sqrt {10}\)
(d) \(\sqrt {11}\)
Solution:
(c) \(\sqrt {10}\)
Hint:
Equation of circle
3x² + by² + 4 bx – 6by + b² = 0
a = b ⇒ b = 3
3x² + 3y² + 12x – 18y + 9 = 0
÷ by 3 x² + y² + 4x – 6y + 3 = 0
2g = 4; 2f = -6; c = 3
g = 2; f = -3
r = \(\sqrt {g^2+f^2-c}\)
= \(\sqrt {4+9-3}\)
= \(\sqrt {10}\)
![]()
Question 6.
The centre of the circle inscribed in a square formed by the lines x² – 8x – 12 = 0 and y² – 14y + 45 = 0 is
(a) (4, 7)
(b) (7, 4)
(c) (9, 4)
(d) (4, 9)
Solution:
(a) (4, 7)
Hint:
Equation of lines
x² – 8x – 12 = 0
(x – 6)(x – 2) = 0
x = 2, 6
Another lines
y² – 14y + 45 = 0
(y – 5 )(y – 9) = 0
y = 5, 9
Hence the extremities of the diameter are (6, 9) and (2, 5).
Centre is mid point of (6, 9) and (2, 5)
Centre = (\(\frac {6+2}{2}\),\(\frac {9+5}{2}\))
= (4, 7)
Question 7.
The equation of the normal to the circle x² + y² – 2x – 2y + 1 = 0 which is parallel to the line 2x + 4y = 3 is
(a) x + 2y = 3
(b) x + 2y + 3 = 0
(c) 2x + 4y + 3 = 0
(d) x – 2y + 3 = 0
Solution:
(a) x + 2y = 3
Hint:
x² + y² – 2x – 2y + 1 = 0
2g = -2 2f = -2
g = -1 f = -1
Parallel line be 2x + 4y + λ = 0
Centre be (-g, -f) = (1, 1)
Which lies on line
2 + 4 + λ = 0 ⇒ λ = -6
∴ 2x + 4y – 6 = 0 ⇒ x + 2y = 3
![]()
Question 8.
If P(x, y) be any point on 16x² + 25y² = 400 with foci F(3, 0) then PF1 + PF2 is
(a) 8
(b) 6
(c) 10
(d) 12
Solution:
(c) 10
Hint:
16x² + 25y² = 400
\(\frac {x^2}{25}\) + \(\frac {y^2}{16}\) = 1
a² = 25
⇒ ∴ a = ±5
PF1 + PF2 = major axis = 2a
= 2 × 5 = 10.
Question 9.
The radius of the circle passing through the points (6,2) two of whose diameter are x + y = 6 and x + 2y = 4 is
(a) 10
(b) 2√5
(c) 6
(d) 4
Solution:
(b) 2√5
Hint:
x + y = 6 …….. (1)
x + 2y = 4 ……… (2)
(1) – (2) -y = 2 ⇒ y = -2
(1) ⇒ x – 2 = 6 ⇒ x = 8.
point be (8, -2)
another point (6, 2)
radius = \(\sqrt {(x_2-x_1)^2+(y_2-y_1)^2}\)
= \(\sqrt {(8-6)^2+(2+2)^2}\)
= \(\sqrt {2^2+4^2}\) = \(\sqrt {4+16}\)
= \(\sqrt {20}\) = 2√5.
![]()
Question 10.
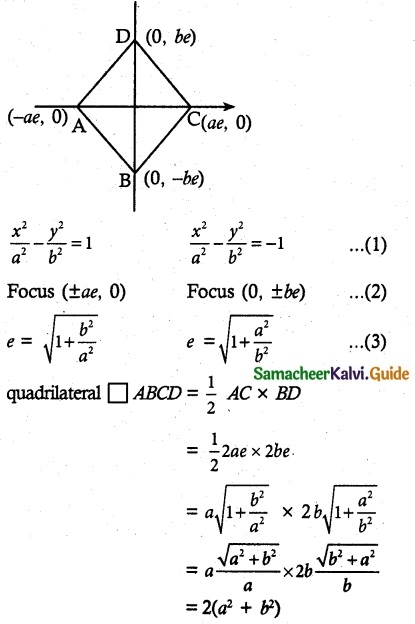
The area of quadrilateral formed with foci of the hyperbolas \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1 and \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = -1 is
(a) 4(a² + b²)
(b) 2(a² + b²)
(c) a² + b²
(d) \(\frac {1}{2}\)(a²+ b²)
Solution:
(b) 2(a² + b²)
Hint:
Question 11.
If the normals of the parabola y² = 4x drawn at the end points of its latus rectum are tangents to the circle (x – 3)² + (y + 2)² = r², then the value of r² is
(a) 2
(b) 3
(c) 1
(d) 4
Solution:
(a) 2
Hint:
y² = 4x
4a = 4
a = 1
End points of latus rectum = (a, ±2a)
= (1, ±2)
Normal equation
xyx + 2ay = x1y1 + 2 ay1
Equation of normal at points (1, ±2)
y = -x + 3, y = x + 3
x + y – 3 = 0, x – y + 3 = 0
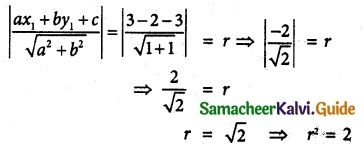
![]()
Question 12.
If x + y = k is a normal to the parabola y² = 12x, then the value of k is 14.
(a) 3
(b) -1
(c) 1
(d) 9
Solution:
(d) 9
Hint:
y² = 12x ⇒ 4a = 12
⇒ a = 3
y = mx + c ∴ x + y = k
⇒ y = -x + k
∴ m = -1, c = k.
c = -2am – am² ⇒ k = -2a(-1) – a(-1)³
k = -6(-1) – 3(-1) = 6 + 3 = 9
k = 9
Question 13.
The ellipse E1 : \(\frac {x^2}{9}\) + \(\frac {y^2}{4}\) = 1 is inscribed in a rectangle R whose sides are parallel to the co-ordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse is
(a) \(\frac {√2}{2}\)
(b) \(\frac {√3}{2}\)
(c) \(\frac {1}{2}\)
(d) \(\frac {3}{4}\)
Solution:
(c) \(\frac {1}{2}\)
Hint:

![]()
Question 14.
Tangents are drawn to, the, hyperbola \(\frac {x^2}{9}\) – \(\frac {y^2}{4}\) = 1 parallel to the straight line 2x – y – 1. One of the points of contact of tangents on the hyperbola is
(a) (\(\frac {9}{2√2}\), \(\frac {-1}{√2}\))
(b) (\(\frac {-9}{2√2}\), \(\frac {1}{√2}\))
(c) (\(\frac {9}{2√2}\), \(\frac {1}{√2}\))
(d) (3√3, -2√2)
Solution:
(c) (\(\frac {9}{2√2}\), \(\frac {1}{√2}\))
Hint:
a² = 9 b² = 4, 2x – y = 1
y = 2x – 1
m = 2

Question 15.
The equation of the circle passing through the foci of the ellipse \(\frac {x^2}{16}\) + \(\frac {y^2}{9}\) = 1 having centre at (0, 3) is
(a) x² + y² – 6y – 7 = 0
(b) x² + y² – 6y + 7 = 0
(c) x² + y² – 6y – 5 = 0
(d) x² + y² – 6y + 5 = 0
Solution:
(a) x² + y² – 6y – 7 = 0
Hint:
a² = 16, b² = 16
(h, k) = (0, 3)
e = \(\sqrt{1-\frac {b^2}{a^2}}\) = \(\sqrt{1-\frac {9}{16}}\)
= \(\sqrt{\frac {7}{16}}\) = \(\frac {√7}{4}\)
ae = 4\(\frac {√7}{4}\) = √7.
F(√7, 0) lies on circle.
(x – h)² + (y – k)² = r²
(√7 – 0)² + (0 – 3)² = r² ⇒ √7² + 3² = r²
7 + 9 = r²
⇒ r² = 16.
∴ (x – 0)² + (y – 3)² = 16
x² + y² – 6y + 9 = 16
x² + y² – 6y – 7 = 0
![]()
Question 16.
Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centered at (0, y) passing through the origin and touching the circle C externally, then the radius of T is equal to
(a) \(\frac {√3}{√2}\)
(b) \(\frac {√3}{2}\)
(c) \(\frac {1}{2}\)
(d) \(\frac {1}{4}\)
Solution:
(d) \(\frac {1}{4}\)
Hint:
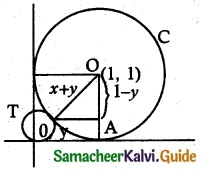
ΔOO’A
(1 + y)² = (1 – y)² + 1
1 + y² + 2y = 1 + y² – 2y + 1
4y = 1 ⇒ y = \(\frac {1}{4}\)
Question 17.
Consider an ellipse whose centre is of the origin and its major axis is a long x-axis. If its eccentricity is \(\frac {3}{5}\) and the distance between its foci is 6, then the area of the quadrilateral’ inscribed in the ellipse with diagonals as major and minor axis, of the ellipse is
(a) 8
(b) 32
(c) 80
(d) 40
Solution:
(d) 40
Hint:

e = \(\frac {3}{5}\)
2ae = 6 ⇒ 2a(\(\frac {3}{5}\)) = 6
a = 5; b = 4
Area = 4 × \(\frac {1}{2}\) × ab = 2 ab
= 2 × 5 × 4
= 40
![]()
Question 18.
Area of the greatest rectangle inscribed in the ellipse \(\frac {x^2}{16}\) + \(\frac {y^2}{9}\) = 1 is
(a) 2ab
(b) ab
(c) \(\sqrt {ab}\)
(d) \(\frac {a}{b}\)
Solution:
(a) 2ab
Hint:

x = a cosθ; y = b sinθ
length = 2acosθ; breadth = 2bsinθ
A = l × b = 4absinθcosθ
A = 2ab sin2θ
\(\frac {dA}{dt}\) = 2ab cos2θ (2)
= 4ab cos2θ
\(\frac {dA}{dt}\) = 0
cos2θ = 0
2θ = \(\frac {π}{2}\)
θ = \(\frac {π}{4}\)
∴ A = 2ab sin²(\(\frac {π}{4}\))
= 2ab sin \(\frac {π}{2}\)
A = 2ab
Question 19.
An ellipse has OB as semi minor axes, F and F’ its foci and the angle FBF’ is a right angle. Then the eccentricity of the ellipse is
(a) \(\frac {1}{√2}\)
(b) \(\frac {1}{2}\)
(c) \(\frac {1}{4}\)
(d) \(\frac {1}{√3}\)
Solution:
(a) \(\frac {1}{√2}\)
Hint:
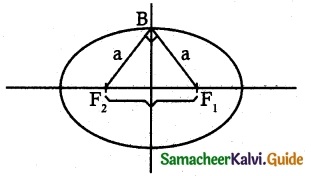
Distance between foci and end of minor axes = a
∴ F1B = F2 = a
F1F2 = 2ae
In right angle F1BF2
F1B² + F2B² = F1F2²
a² + a² = (2ae)²
2a² = 4a²e²
e² = \(\frac {2}{4}\) = \(\frac {1}{2}\)
∴ e = \(\frac {1}{√2}\)
![]()
Question 20.
The eccentricity of the ellipse
(x – 3)² + (y – 4)² = \(\frac {y²}{9}\) is
(a) \(\frac {√3}{2}\)
(b) \(\frac {1}{3}\)
(c) \(\frac {1}{3√2}\)
(d) \(\frac {1}{√3}\)
Solution:
(b) \(\frac {1}{3}\)
Hint:
PF = e²p³
(x – h)² + (y – k)² = e²(\(\frac {ax+by+c}{\sqrt{a^2+b^2}}\))
(h, k) = (3, 4),
a = 0, c = 0
e² = \(\frac {1}{3}\)
e = \(\frac {1}{3}\)
Question 21.
If the two tangents drawn from a point P to the parabola y2 = 4r are at right angles then the locus of P is {SEA
(a) 2x + 1 = 0
(b) x = -1
(c) 2x – 1 = 0
(d) x = 1
Solution:
(b) x = -1
Hint:
Locus of P = Directrix of y² = 4x; 4a = 4
∴ a = 1
Equation of directrix x = -a = -1
∴ -x = -1
![]()
Question 22.
The circle passing through (1, -2) and touching the axis of x at (3, 0) passing through the point
(a) (-5, 2)
(b) (2, -5)
(c) (5, -2)
(d) (-2, 5)
Solution:
(c) (5, -2)
Hint:
(x – 3)² + (y – 0)² + λy = 0
At (1, -2), (1 – 3)² + (-2 – 0)² + λy = 0
4 + 4 – 2λ = 0
8 = 2λ
λ = 4
x² – 6x + 9 + y² + 4y = 0
Apply all the point which satisfied that passes through the circle At (+5, -2),
25 – 30 + 9 + 4 – 8 = 0
Question 23.
The locus of a point whose distance from (- 2, 0) is \(\frac {2}{3}\) times its distance from the line x = \(\frac {-9}{2}\) is
(a) a parabola
(b) a hyperbola
(c) an ellipse
(d) a circle
Solution:
(c) an ellipse
Hint:
P(h, k) Q(-2, 0)
x = –\(\frac {9}{2}\) PQ = \(\frac {2}{3}\)
2x + 9 = 0
\(\sqrt {(h+2)^2+k^2}\) = \(\frac {2}{3}\)|\(\frac {2h+9}{2}\)|
(h + 2)² + k² = \(\frac {1}{9}\)(2h + 9)²
h² + 4 + 4h + k² = \(\frac {1}{9}\)(4h² + 36h + 81)
9h² + 36 + 36h + 9k² = 4h² + 36h + 81
5h² + 9k² = 45
\(\frac {h^2}{9}\) + \(\frac {k^2}{5}\) = 1
\(\frac {x^2}{9}\) + \(\frac {y^2}{5}\) = 1
Which is ellipse.
![]()
Question 24.
The values of m for which the line y = mx + 2√5 touches the hyperbola 16x² – 9y² = 144 are the roots of x² – (a + b)x – 4 = 0, then the value of (a + b) is
(a) 2
(b) 4
(c) 0
(d) -2
Solution:
(c) 0
Hint:
a² = 9; b² = 16
a = 3; b = 4
c² = a²m² – b²
(2√5)² = 9m² – 16
20 + 16 = 9m²; m² = \(\frac {36}{9}\)
∴ m = 2 which is roots of x² -(a + b)x – 4 = 0
2² -(a + b)2 – 4 = 0
a + b = 0
Question 25.
If the coordinates at one end of a diameter of the circle x² + y² – 8x – 4y + c = 0 are (11, 2) the cordinates of the other end are
(a) (-3, 2)
(b) (2, -5)
(c) (5, -2)
(d) (-2, 5)
Solution:
(a) (-3, 2)
Hint:

2g = -g; 2f = -4
g = -4; f = -2
c(-g, -f) = (4, 2)
\(\frac {x_1+x_2}{9}\) = 4; \(\frac {y_1+y_2}{2}\) = 2
\(\frac {x_1+11}{2}\) = 4; \(\frac {y_1+2}{2}\) = 2
x1 = 8 – 11; y1 = 4 – 2
x1 = -3; y1 = 2
∴ Other end be (-3, 2)
![]()