Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.10 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.10
Choose the most suitable answer from the given four alternatives:
Question 1.
The volume of a sphere is increasing in volume at the rate of 3π cm³/ sec. The rate of change of its radius when radius is \(\frac { 1 }{ 2 }\) cm
(a) 3 cm/s
(b) 2 cm/s
(c) 1 cm/s
(d) \(\frac { 1 }{ 2 }\) cm/s
Solution:
(a) 3 cm/s
Hint:
Volume V = \(\frac { 4 }{ 3 }\) πr³
Given \(\frac { dV }{ dt }\) = 3π cm³/sec
Differentiating w.r.t. ‘t’ r = \(\frac { 1 }{ 2 }\) cm

Rate of change of radius is 3 cm/sec.
![]()
Question 2.
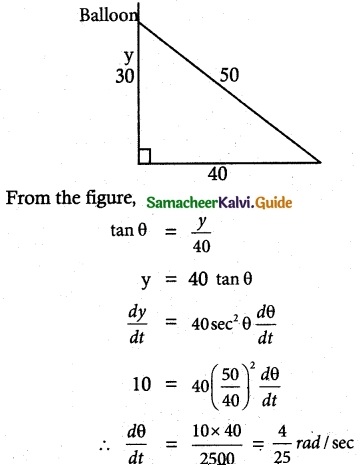
A balloon rises straight up at 10 m/s. An observer is 40 m away from the spot where the balloon left the ground. Find the rate of change of the balloon’s angle of elevation in radian per second when the balloon is 30 metres above the ground.
(a) \(\frac { 3 }{ 25 }\) radan/sec
(b) \(\frac { 4 }{ 25 }\) radian/sec
(c) \(\frac { 1 }{ 5 }\) radian/sec
(d) \(\frac { 1 }{ 3 }\) radian/sec
Solution:
(b) \(\frac { 4 }{ 25 }\) radian/sec
Hint:
![]()
Question 3.
The position of a particle moving along a horizontal line of any time t is given by s(t) = 3t² – 2t – 8. The time at which the particle is at rest is
(a) t = 0
(b) t = \(\frac { 1 }{ 3 }\)
(c) t = 1
(d) t = 3
Solution:
(b) t = \(\frac { 1 }{ 3 }\)
Hint:
s(t) = 3t² – 2t – 8
Velocity V = \(\frac { ds }{ dt }\) = 6t – 2
When the particle comes to rest,
velocity V = 0
6t – 2 = 0
t = \(\frac { 1 }{ 3 }\)
Question 4.
A stone is thrown, up vertically. The height reaches at time t seconds is given by x = 80t – 16t². The stone reaches the maximum! height in time t seconds is given by
(a) 2
(b) 2.5
(c) 3
(d) 3.5
Solution:
(b) 2.5
Hint:
x = 80t – 16t²
Velocity V = \(\frac { ds }{ dt }\) = 80 – 32t
When it reaches the maximum height
V = 0 ⇒ 80 – 32t = 0
t = \(\frac { 80 }{ 32 }\) = 2.5
![]()
Question 5.
Find the point on the curve 6y = x³ + 2 at which y-coordinate changes 8 times as fast as x-coordinate is
(a) (4, 11)
(b) (4, -11)
(c) (-4, 11)
(d) (-4, -11)
Solution:
(a) (4, 11)
Hint:

x = ±4
When x = 4, y = 11
∴ Point on the curve is (4, 11).
Question 6.
The abscissa of the point on the curve f(x) = \(\sqrt { 8-2x }\) at which the slope of the tangent is -0.25?
(a) -8
(b) -4
(c) -2
(d) 0
Solution:
(b) -4
Hint:
f(x) = \(\sqrt { 8-2x }\)
f'(x) = –\(\frac { 2 }{ 2\sqrt { 8-2x } }\) = –\(\frac { 1 }{ \sqrt { 8-2x } }\)
Slope of the tangent is – 0.25
ie„ f'(x) = -0.25
–\(\frac { 1 }{ \sqrt { 8-2x } }\) = -0.25 = \(\frac { -1 }{ 4 }\)
\(\sqrt { 8-2x }\) = 4
8 – 2x = 16
x = –\(\frac { 8 }{ 2 }\) = -4
Abscissa x = -4
![]()
Question 7.
The slope of the line normal to the curve f(x) = 2 cos 4x at x = \(\frac { π }{ 12 }\) is
(a) -4√3
(b) -4
(c) –\(\frac { √3 }{ 12 }\)
(d) 4√3
Solution:
(c) –\(\frac { √3 }{ 12 }\)
Hint:
f(x) = 2 cos 4x
f'(x) = -8 sin 4x
Slope of the normal at x = \(\frac { π }{ 12 }\) is
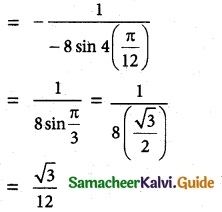
Question 8.
The tangent to the curve y² – xy + 9 = 0 is vertical when
(a) y = 0
(b) y = ±√3
(c) –\(\frac { 1 }{ 2 }\)
(d) y = ±3
Solution:
(d) y = ±3
Hint:
y² – xy + 9 = 0 ……… (1)
2y\(\frac { dy }{ dx }\) – (x\(\frac { dy }{ dx }\) + y) = 0
\(\frac { dy }{ dx }\) (2y – x) = y
\(\frac { dy }{ dx }\) = \(\frac { y }{ 2y-x }\)
When the tangent is vertical \(\frac { dy }{ dx }\) = ∞
i.e., \(\frac { y }{ 2y-x }\) = \(\frac { 0 }{ 1 }\)
⇒ 2y – x = 0
2y = x
sub in (1)
y² – 2y² + 9 = 0
⇒ y² = 9
y = ±3
![]()
Question 9.
The angle between y² = x and x² = y at the origin is
(a) tan-1 \(\frac { 3 }{ 4 }\)
(b) tan-1 (\(\frac { 4 }{ 3 }\))
(c) \(\frac { π }{ 2 }\)
(d) \(\frac { π }{ 4 }\)
Solution:
(c) \(\frac { π }{ 2 }\)
Hint:
y² = x and x² = y are the standard forms of parabolas for which y-axis and x-axis are the two tangents respectively.
Angle between x-axis and y-axis is \(\frac { π }{ 2 }\)
Question 10.
The value of the limit \(\lim _{x \rightarrow 0}\) (cot x – \(\frac { 1 }{ x }\)) is
(a) 0
(b) 1
(c) 2
(d) ∞
Solution:
(d) ∞
Hint:
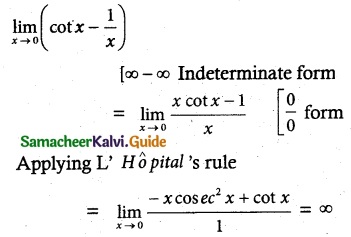
![]()
Question 11.
The function sin4 x + cos4 x is increasing in the interval
(a) [ \(\frac { 5π }{ 8 }\), \(\frac { 3π }{ 4 }\) ]
(b) [ \(\frac { π }{ 2 }\), \(\frac { 5π }{ 8 }\) ]
(c) [ \(\frac { π }{ 4 }\), \(\frac { π }{ 2 }\) ]
(d) [ 0, \(\frac { π }{ 4 }\) ]
Solution:
(c) [ \(\frac { π }{ 4 }\), \(\frac { π }{ 2 }\) ]
Hint:
f(x) = sin4x + cos4x
f'(x) = 4 sin³ x cos x – 4 cos³ x sin x
f'(x) = 0 ⇒ 4 sin x cos x (sin²x – cos²x) = 0
sin x = 0; cos x = 0; sin² – cos² x = 0
x = 0; x = \(\frac { π }{ 2 }\); sin² x = cos² x
x = \(\frac { π }{ 4 }\)
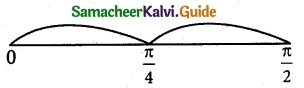
In [0, \(\frac { π }{ 2 }\) ], f'(x) = -ve ⇒ f(x) is decreasing
In [ \(\frac { π }{ 2 }\), \(\frac { π }{ 2 }\) ], f'(x) = +ve ⇒ f(x) is increasing
Question 12.
The number is given by Rolle’s theorem for the function x³ – 3x², x ∈ [0, 3] is
(a) 1
(b) √2
(c) \(\frac { 3 }{ 2 }\)
(d) 2
Solution:
(d) 2
Hint:
f(x) = x³ – 3x²
f'(x) = 3x² – 6x
f'(x) = 0
⇒ 3x (x – 2) = 0
x = 0, 2
![]()
Question 13.
The number given by the Mean value theorem for the function \(\frac { 1 }{ x }\), x ∈ [1, 9] is
(a) 2
(b) 2.5
(c) 3
(d) 3.5
Solution:
(c) 3
Hint:
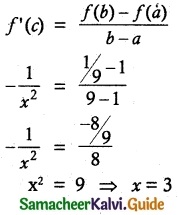
Question 14.
The minimum value of the function |3 – x| + 9 is
(a) 0
(b) 3
(c) 6
(d) 9
Solution:
(d) 9
Hint:
f(x) = |3 – x | + 9
Minimum value of |3 – x | = 0
Minimum value of |3 – x| + 9 = 0 + 9 = 9 and No Maximum value.
![]()
Question 15.
The maximum slope of the tangent to the curve y = ex sin x, x ∈ [0, 2π] is at
(a) x = \(\frac { π }{ 4 }\)
(b) x = \(\frac { π }{ 2 }\)
(c) x = π
(d) x = \(\frac { 3π }{ 2 }\)
Solution:
(b) x = \(\frac { π }{ 2 }\)
Hint:
y = ex sin x, x ∈ [0, 2π] dy
Slope ‘S’ = \(\frac { dy }{ dx }\) = ex cos x + ex sin x
S = ex (cos x + sin x)
\(\frac { dS }{ dx }\) = ex (-sin x + cos x) + (cos x + sin x)ex
= ex (2 cos x)
For maximum or minimum,
\(\frac { dS }{ dx }\) = 0 ⇒ 2ex cos x = 0
ex = 0 is not possible
∴ cos x = 0
x = \(\frac { π }{ 2 }\)
Question 16.
The maximum value of the function x² e-2x, x > 0 is
(a) \(\frac { 1 }{ e }\)
(b) \(\frac { 1 }{ 2e }\)
(c) \(\frac { 1 }{ e^2 }\)
(d) \(\frac { 4 }{ e^4 }\)
Solution:
(c) \(\frac { 1 }{ e^2 }\)
Hint:
Let f(x) = x²e-2x, x > 0
f'(x) = -2x² e-2x + e-2x (2x)
f'(x) = 0 ⇒ -2xe-2x(x – 1) = 0
x = 0 and x = 1
f(x) attains maximum at x = 1 as f”(x) < 0
when x = 1
∴ Maximum value f(1) = (1)² e-2 = \(\frac { 1 }{ e^2 }\)
![]()
Question 17.
One of the closest points on the curve x² – y² = 4 to the point (6, 0) is
(a) (2, 0)
(b) (√5, 1)
(c) (3, √5)
(d) (\(\sqrt { 13 }\), -√3)
Solution:
(c) (3, √5)
Hint:
x² – y² = 4
y² = x² – 4
y = ±\(\sqrt { x^2-4 }\)
Any point on the curve is (x, ± \(\sqrt { x^2-4 }\))
Distance between (6, 0) and (x, ± \(\sqrt { x^2-4 }\)) is \(\sqrt { (x-6)^2+x^2-4 }\)
Substituting all’ the given options, we get minimum distance.
∴ Required point is (3, √5)
Question 18.
The maximum value of the product of two positive numbers’, when their sum of the squares is 200, is
(a) 100
(b) 25√7
(c) 28
(d) 24\(\sqrt { 14 }\)
Solution:
(a) 100
Hint:
Given x² + y² = 200
y² = 200 – x²
y = \(\sqrt { 200-x^2 }\)
Product P = xy = x\(\sqrt { 200-x^2 }\)
\(\frac { dP }{ dx }\) = \(\frac { x(-2x) }{ 2\sqrt{200-x^2} }\) + \(\sqrt{200-x^2}\) …. (1)
\(\frac { dP }{ dx }\) = 0 ⇒ -2x² + 200 = 0
x² = 100
x = 10
∴ y = \(\sqrt{200-100}\) = 10
∴ Maximum product is P = xy
= (10) (10)
= 100
![]()
Question 19.
The curve y = ax4 + bx² with ab > 0
(a) has no horizontal tangent
(b) is concave up
(c) is concave down
(d) has no points of inflection
Solution:
(d) has no points of inflection
Hint:
y = ax4 + bx²
\(\frac { dy }{ dx }\) = 4ax³ + 2bx
\(\frac { d^2y }{ dx^2 }\) = 12ax² + 2b
\(\frac { d^2y }{ dx^2 }\) = 0 ⇒ 12ax² + 2b = 0
x² = –\(\frac { b }{ 6a }\)
x is unreal.
Hence no points of inflection.
Question 20.
The point of inflection of the curve y = (x – 1)³ is
(a) (0, 0)
(b) (0, 1)
(c) (1, 0)
(d) (1, 1)
Solution:
(c) (1, 0)
Hint:
y = (x – 1)³
\(\frac { dy }{ dx }\) = 3(x – 1)²
\(\frac { d^2y }{ dx^2 }\) = 6(x – 1)
\(\frac { d^2y }{ dx^2 }\) = 0 ⇒ 6(x – 1) = 0
x = 1
y = f(x)
\(\frac { dy }{ dx }\) = f'(x)
\(\frac { d^2y }{ dx^2 }\) = f”(x)
In (-∞, 1), f”(x) < 0, curve is concave down In (1, ∞), f”(x) > 0, curve is concave up
f”(x) changes its sign when passing through x = 1
when x = 1, y = 0
∴ (1, 0) is the point of inflection.
![]()