Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.2 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.2
Question 1.
Find the slope of the tangent to the following curves at the respective given points.
(i) y = x4 + 2x² – x at x = 1
(ii) x = a cos³ t, y = b sin³ t at t = \(\frac { π }{ 2 }\)
Solution:
(i) y = x4 + 2x² – x
Differentiating w.r.t. ‘x’
\(\frac { dy }{ dx }\) = 4x³ + 4x – 1
Slope of the tangent (\(\frac { dy }{ dx }\))(x=1)
= 4(1)³ + 4(1) – 1
= 4 + 4 – 1 = 7
(ii) x = a cos³ t, y = b sin³ t
Differenriating w.r.t. ‘t’
\(\frac { dx }{ dt }\) = – 3a cos² t sin t
\(\frac { dy }{ dt }\) = 3b sin² t sin t
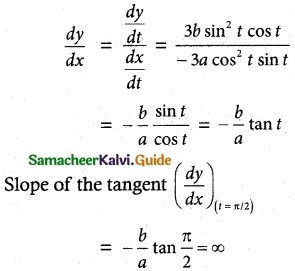
![]()
Question 2.
Find the point on the curve y = x² – 5x + 4 at which the tangent is parallel to the line 3x + y = 7.
Solution:
y = x² – 5x + 4
Differentiating w.r.t. ‘x’
Slope of the tangent \(\frac { dy }{ dx }\) = 2x – 5
Given line 3x + y = 7
Slope of the line = –\(\frac { 3 }{ 1 }\) = -3
Since the tangent is parallel to the line, their slopes are equal.
∴ \(\frac { dy }{ dx }\) = -3
⇒ 2x – 5 = -3
2x = 2
x = 1
When x = 1, y = (1)² – 5 (1) + 4 = 0
∴ Point on the curve is (1, 0).
Question 3.
Find the points on curve y = x³ – 6x² + x + 3 where the normal is parallel to the line x + y = 1729.
Solution:
y = x³ – 6x² + x+ 3
Differentiating w.r.t. ‘x’
Slope of the tangent \(\frac { dy }{ dx }\) = 3x² – 12x + 1
Slope of the normal = \(\frac { 1 }{ 3x^2 – 12x + 1 }\)
Given line is x + y = 1729
Slope of the line is – 1
Since the normal is parallel to the line, their slopes are equal.
\(\frac { 1 }{ 3x^2 – 12x + 1 }\) = -1
3x² – 12x + 1 = 1
3x² – 12x =0
3x(x – 4) = 0
x = 0, 4
When x = 0, y = (0)³ – 6(0)² + 0 + 3 = 3
When x = 4, y = (4)³ – 6(4)² + 4 + 3
= 64 – 96 + 4 + 3 = -25
∴ The points on the curve are (0, 3) and (4, -25).
![]()
Question 4.
Find the points on the curve y² – 4xy = x² + 5 for which the tangent is horizontal.
Solution:
y² – 4xy = x² + 5 ………… (1)
Differentiating w.r.t. ‘x’
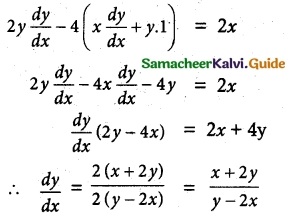
When the tangent is horizontal(Parallel to X-axis) then slope of the tangent is zero.
\(\frac { dy }{ dx }\) = 0 ⇒ \(\frac { x+2y }{ y-2x }\) = 0
⇒ x + 2y = 0
x = -2y
Substituting in (1)
y² – 4 (-2y) y = (-2y)² + 5
y² + 8y² = 4y² + 5
5y² = 5 ⇒ y² = 1
y = ±1
When y = 1, x = -2
When y = – 1, x = 2
∴ The points on the curve are (- 2, 1) and (2, -1).
![]()
Question 5.
Find the tangent and normal to the following curves at the given points on the curve.
(i) y = x² – x4 at (1, 0)
(ii) y = x4 + 2ex at (0, 2)
(iii) y = x sin x at (\(\frac { π }{ 2 }\), \(\frac { π }{ 2 }\))
(iv) x = cos t, y = 2 sin² t at t = \(\frac { π }{ 3 }\)
Solution:
(i) y = x² – x4 at (1, 0)
Differentiating w.r.t. ‘x’
\(\frac { dx }{ dy }\) = 2x – 4x³
Slope of the tangent ‘m’ = (\(\frac { dx }{ dy }\))(1, 0)
= 2 (1) – 4 (1)³ = -2
Slope of the normal –\(\frac { 1 }{ m }\) = \(\frac { -1 }{ -2 }\) = \(\frac { 1 }{ 2 }\)
Equation of tangent is
y – y1 = m (x – x1)
y – 0 = – 2 (x – 1)
y = -2x + 2
2x + y – 2 = 0
Equation of Normal is
y – y1 = –\(\frac { 1 }{ m }\)(x – x1)
y – 0 = \(\frac { 1 }{ 2 }\)(x – 1)
2y = x- 1
x – 2y – 1 = 0
(ii) y = x4 + 2ex at (0, 2)
Differentiating w.r.t. ‘x’
\(\frac { dy }{ dx }\) = 4x3 + 2ex
Slope of the tangent ‘m’
(\(\frac { dy }{ dx }\))(0, 2) = 4(0)³ + 2e0 = 2
Slope of the Normal –\(\frac { 1 }{ m }\) =-\(\frac { 1 }{ 2 }\)
Equation of tangent is
y – y1 = m(x – x1)
⇒ y – 2 = 2(x – 0)
⇒ y – 2 = 2x
⇒ 2x – y + 2 = 0
Equation of Normal is
y – y1 = –\(\frac { 1 }{ m }\) (x – x1)
y – 2 = –\(\frac { 1 }{ 2 }\)(x – 0)
2y – 4 = -x
x + 2y – 4 = 0
(iii) y = x sin x at (\(\frac { π }{ 2 }\), \(\frac { π }{ 2 }\))
Differentiating w.r.t. ‘x’
\(\frac { dy }{ dx }\) = x cos x + sin x
Slope of the tangent ‘m’ = (\(\frac { dy }{ dx }\))(π/2, π/2)
= \(\frac { π }{ 2 }\) cos \(\frac { π }{ 2 }\) + sin \(\frac { π }{ 2 }\) = 1
Slope of the Normal –\(\frac { 1 }{ m }\) = -1
Equation of tangent is
y – y1 = m(x – x1)
⇒ y – \(\frac { π }{ 2 }\) = 1 (x – \(\frac { π }{ 2 }\))
⇒ x – y = 0
Equation of Normal is
y – y1 = –\(\frac { 1 }{ m }\)(x – x1)
⇒ y – \(\frac { π }{ 2 }\) = -1(x – \(\frac { π }{ 2 }\))
⇒ y – \(\frac { π }{ 2 }\) = -x + \(\frac { π }{ 2 }\)
⇒ x + y – π = 0
![]()
(iv) x = cos t, y = 2 sin² t at t = \(\frac { π }{ 2 }\)
at t = \(\frac { π }{ 3 }\), x = cos \(\frac { π }{ 3 }\) = \(\frac { 1 }{ 2 }\)
at t = \(\frac { π }{ 3 }\), y = 2 sin² \(\frac { π }{ 3 }\) = 2(\(\frac { 3 }{ 4}\)) = \(\frac { 3 }{ 2 }\)
Point is (\(\frac { 1 }{ 2 }\), \(\frac { 3 }{ 2 }\))
Now x = cos t y = 2 sin² t
Differentiating w.r.t. ‘t’,
\(\frac { dx }{ dt }\) = -sin t; \(\frac { dy }{ dt }\) = 4 sin t cos t
Slope of the tangent
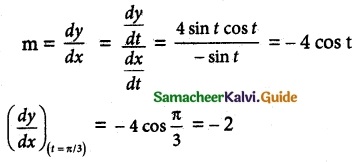
Slope of the Normal –\(\frac { 1 }{ m }\) = \(\frac { 1 }{ 2 }\)
Equation of tangent is
y – y1 = m(x – x1)
⇒ y – \(\frac { 3 }{ 2 }\) = -2(x – \(\frac { 1 }{ 2 }\))
⇒ 2y – 3 = – 4x + 2
⇒ 4x + 2y – 5 = 0
Equation of Normal is
y – y1 = –\(\frac { 1 }{ m }\)(x – x1)
⇒ y – \(\frac { 3 }{ 2 }\) = \(\frac { 1 }{ 2 }\)(x – \(\frac { 1 }{ 2 }\))
⇒ 2 (2y – 3) = 2x – 1
⇒ 4y – 6 = 2x – 1
⇒ 2x – 4y + 5 = 0
Question 6.
Find the equations of the tangents to the curve y = 1 + x³ for which the tangent is orthogonal with the line x + 12y = 12.
Solution:
Curve is y = 1 + x³
Differentiating w.r.t ‘x’,
Slope of the tangent ‘m’ = \(\frac { dy }{ dx }\) = 3x²
Given line is x + 12y = 12
Slope of the line is –\(\frac { 1 }{ 12 }\)
Since the tangent is orthogonal with the line, the slope of the tangent is 12.
∴ \(\frac { dy }{ dx }\) = 12
i.e 3x² = 12
x² = 4
x = ±2
When x = 2, y = 1 + 8 = 9 ⇒ point is (2, 9)
When x = -2, y = 1 – 8 = -7 ⇒ point is (-2, -7)
Equation of tangent with slope 12 and at the j point (2, 9) is
y – 9 = 12 (x – 2)
y – 9 = 12x – 24
12x – y – 15 = 0
Equation of tangent with slope 12 and at the point (-2, -7) is
y + 7 = 12 (x + 2)
y + 7 = 12x + 24
12x – y + 17 = 0
![]()
Question 7.
Find the equations of the tangents to the curve y = –\(\frac { x+1 }{ x-1 }\) which are parallel to the line x + 2y = 6.
Solution:
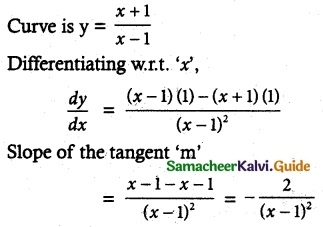
Given line is x + 2y = 6
Slope of the line = –\(\frac { 1 }{ 2 }\)
Since the tangent is parallel to the line, then the slope of the tangent is –\(\frac { 1 }{ 2 }\)
∴ \(\frac { dy }{ dx }\) = \(\frac { 2 }{ (x-1)^2 }\) = –\(\frac { 1 }{ 2 }\)
(x – 1)² = 4
x – 1 = ±2
x = -1, 3
When x = – 1, y = 0 ⇒ point is (-1, 0)
When x = 3, y = 2 ⇒ point is (3, 2)
Equation of tangent with slope –\(\frac { 1 }{ 2 }\) and at the point (-1, 0) is
y – o = –\(\frac { 1 }{ 2 }\)(x + 1)
2y = -x – 1 ⇒ x + 2y + 1 = 0
Equation of tangent with slope –\(\frac { 1 }{ 2 }\) and at the point (3, 2) is 2
y – 2 = –\(\frac { 1 }{ 2 }\) (x – 3)
2y – 4 = -x + 3
x + 2y – 7 = 0.
Question 8.
Find the equation of tangent and normal to the curve given by x – 7 cos t andy = 2 sin t, t ∈ R at any point on the curve.
Solution:
x = 7 cos t and y = 2 sin t, t ∈ R
Differentiating w.r.t. ‘t’,
\(\frac { dx }{ dt }\) = -7 sin t and \(\frac { dy }{ dt }\) = 2 cos t
Slope of the tangent ‘m’
\(\frac { dy }{ dx }\) = \(\frac{\frac { dy }{ dt }}{\frac{ dx }{ dt }}\) = \(\frac { 2 cot t }{ -7 sin t }\)
Any point on the curve is (7 Cos t, 2 sin t)
Equation of tangent is y – y1 = m (x – x1)
y – 2 sint = –\(\frac { 2 cot t }{ 7 sin t }\) (x – 7 cos t)
7y sin t – 14 sin² t = -2x cos t + 14 cos² t
2x cos t + 7 y sin t – 14 (sin² t + cos² t) = 0
2x cos t + 7y sin t – 14 = 0
Now slope of normal is –\(\frac { 1 }{ 3 }\) = \(\frac { 7 sin t }{ 2 cos t }\)
Equation of normal is y – y1 = –\(\frac { 1 }{ m }\)(x – x1)
y – 2 sin t = \(\frac { 7 sin t }{ 2 cos t }\) (x – 7 cos t)
2y cos t – 4 sin t cos t = 7x sin t – 49 sin t cos t 7x sin t – 2y cos t – 45 sin t cos t = 0
![]()
Question 9.
Find the angle between the rectangular hyperbola xy = 2 and the parabola x² + 4y = 0
Solution:
Given curves are xy = 2 ……… (1)
x² + 4y = 0 ………. (2)
Now solving (1) and (2)
Substituting (1) in (2)
⇒ x² + 4(2/x) = 0
x³ + 8 = 0
x³ = -8
x = -2
Substituting in (1) ⇒ y = \(\frac { 2 }{ -2 }\) = -1
∴ Point of intersection of (1) and (2) is (-2, -1)
xy = 2 ⇒ y = \(\frac { 2 }{ x }\) ……….. (1)
Differentiating w.r.t. ‘x’

The angle between the curves
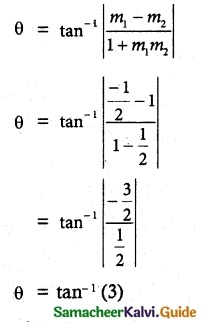
Question 10.
Show that the two curves x² – y² = r² and xy = c² where c, r are constants, cut orthogonally.
Solution:
Given curves are x² – y² = r² ……….. (1)
xy = c² …….. (2)
Let (x1, y1) be the point of intersection of the given curves.
(1) ⇒ x² – y² = r²
Differentiating w.r.t ‘x’,
2x – 2y \(\frac { dx }{ dy }\) = 0
\(\frac { dx }{ dy }\) = \(\frac { x }{ y }\)
now (\(\frac { dx }{ dy }\))(x1,y1) = m1 = \(\frac { x_1 }{ y_1 }\)
(2) ⇒ xy = c²
Differentiating w.r.t ‘x’,

Hence, the given curves cut orthogonally.
![]()