Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.8 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.8
Question 1.
Find two positive numbers whose sum is 12 and their product is maximum.
Solution:
Let the two numbers be x, 12 – x.
Their product p = x (12 – x) = 12x – x2
To find the maximum product.
p'(x) = 12 – 2x
p”(x) = -2
p'(x) = 0 ⇒ 12 – 2x = 0 ⇒ 2x = 12
⇒ x = 6
at x = 6, p”(x) = -2 = -ve
⇒ p is maximum at x = 6
when x = 6, 12 – x = 12 – 6 = 6
So the two numbers are 6, 6
![]()
Question 2.
Find two positive numbers whose product is 20 and their sum is minimum.
Solution: Let the two positive numbers be ‘x’ and ‘y’
Given product is 20 ⇒ xy = 20 ⇒ y = \(\frac { 20 }{ x }\)
Sum S = x + y
S = x + \(\frac { 20 }{ x }\)
\(\frac { dS }{ dx }\) = 1 – \(\frac { 20 }{ x^2 }\)
For maximum or minimum, \(\frac { dS }{ dx }\) = 0
x² – 20 = 0 x² = 20
x = ±2√5
[x= -2√5 is not possible
\(\frac { d^2S }{ dx^2 }\) = \(\frac { 40 }{ x^3 }\)
at x = 2√5, \(\frac { d^2S }{ dx^2 }\) > 0
∴ Sum ‘S’ is minimum when x = 2√5
y = \(\frac { 20 }{ 2√5 }\) = 2√5
Minimum sum = 2√5 + 2√5 = 4√5
Question 3.
Find the smallest possible value of x² + y² given that x + y = 10.
Solution:
Given x + y = 10 ⇒ y = 10 – x
Let A = x² + y²
A = x² + (10 – x)²
\(\frac { dA }{ dx }\) = 2x + 2(10 – x)(-1)
For maximum or minimum,
\(\frac { dA }{ dx }\) = 0 ⇒ 2(2x – 10) = 0
x = 5
\(\frac { d^2A }{ dx^2 }\) = 4
at x = 5, \(\frac { d^2A }{ dx^2 }\) > 0
∴ A is minimum when x = 5
y = 10 – 5 = 5
∴ The smallest possible value of x² + y² is
(5)² + (5)² = 25 + 25 = 50
![]()
Question 4.
A garden is to be laid out in a rectangular area and protected by a wire fence. What is the largest possible area of the fenced garden with 40 meters of wire?
Solution:
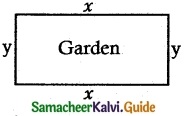
Perimeter = 40 m
2(l + b) = 40 ⇒ l + b = 20
Let l = x m
b = (20 – x)m
Area = l × b = x(20 – x) = 20x – x2
To find the maximum area
A(x) = 20x – x2
A'(x) = 20 – 2x
A”(x) = -2
A'(x) = 0 ⇒ 20 – 2x = 0
⇒ x = 10
x = 10 is a maximum point
:. Maximum Area = x (20 – x)
= 10(20 – 10)
= 10 × 10 = 100 sq.m.
Question 5.
A rectangular page is to contain 24 cm² of print. The margins at the top and bottom of the page are 1.5 cm and the margins at the other sides of the page are 1 cm. What should be the dimensions’ of the page so that the area of the paper used is minimum?
Solution:
Let the width of the printed part be ‘x’ cm
Let the height Of the printed part be ‘y’ cm
Given, Area of the printed part = 24 cm²
i.e., xy = 24
y = \(\frac { 24 }{ x }\)
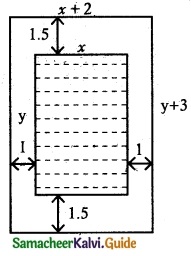
From the given data,
Width of the page
= x + 2(1) = x + 2 cm
Height of the page
= y + 2(1.5) = y + 3 cm
∴ Area of the paper
‘A’ = (x + 2) (y + 3)
= (x + 2) (\(\frac { 24 }{ x }\) + 3)
A = 24 + 3x + \(\frac { 48 }{ x }\) + 6
\(\frac { dA }{ dx }\) = 3 – \(\frac { 48 }{ x^2 }\)
For maximum or minimum,
\(\frac { dA }{ dx }\) = 0
3x² – 48 = 0
x² = 16
x = ±4 [∵ x cannot be negative
∴ x = 4
Now, \(\frac { d^2A }{ dx^2 }\) = \(\frac { 96 }{ x^3 }\)
at x = 4, \(\frac { d^2A }{ dx^2 }\) > 0
∴ Area is minimum when x = 4
y = \(\frac { 24 }{ 4 }\) = 6
∴ Dimensions of the page:
Width of the page = x + 2 = 4 + 2 = 6 cm
Height of the page = y + 3 = 6 + 3 = 9 cm
![]()
Question 6.
A farmer plans to fence a rectangular pasture adjacent to a river. The pasture must contain 1,80,000 sq. mtrs in order to provide enough grass for herds. No fencing is needed along the river. What is the length of the minimum needed fencing material?
Solution:

Let the length of the pasture be ‘x’ m
Let the breadth of the pasture be ‘y’ m
Given Area = 1,80,000
xy = 1,80,000
y = 1,80,000
For fencing, we need 2y + x
(one side is River)
Let P = 2y + x
P = 2(\(\frac { 180000 }{ 2 }\)) + x = \(\frac { 360000 }{ x }\) + x
\(\frac { dP }{ dx }\) = –\(\frac { 360000 }{ x^2 }\) + 1
For maximum or minimum,
\(\frac { dP }{ dx }\) = 0
⇒ – 360000 + x² = 0
x² = 360000
x = ±600
[x = -600 is not possible]
∴ x = 600
Now, \(\frac { d^2P }{ dx^2 }\) = \(\frac { 720000 }{ x^3 }\)
at x = 600, \(\frac { d^2P }{ dx^2 }\) > 0
∴ P is minimum when x = 600
y = \(\frac { 180000 }{ 600 }\) = 300
∴ Length of the minimum needed fencing material = 2y + x = 2(300) + 600 = 1200 m
Question 7.
Find the dimensions of the rectangle with the maximum area that can be inscribed in a circle of a radius of 10 cm.
Solution:
Let the length of the rectangle be ‘x’ cm
The breadth of the rectangle be ‘y’ cm
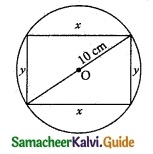
From the figure,
x² + y² = (20)² [Pythagoras Theorem
y² = 400 – x²
[∵ radius of the circle is 10 cm
y = \(\sqrt { 400-x^2 }\)
Now, Axea of the rectangle A = xy
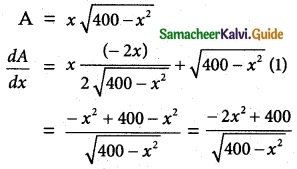
For maximum or minimum,
\(\frac { dA }{ dx }\) = 0 ⇒ \(\frac { -2x^2+400 }{ \sqrt{400-x^2} }\)
x² = 200
x = ±10√2
x = -10√2 is not possible
∴ x = 10√2

Area of the rectangle is maximum When x = 10√2
y = \(\sqrt { 400-200 }\) = \(\sqrt { 200 }\) = 10√2
∴ x = y = 10√2
Length of the rectangle = 10√2 cm
Breadth of the rectangle = 10√2 cm
(Note: A largest rectangle that can be inscribed in a circle is a square)
![]()
Question 8.
Prove that among all the rectangles of the given perimeter, the square has the maximum area.
Solution:
Let x, y be the length and breadth of a rectangle and given perimeter is P (say)
ie. 2(x + y) = P
y = \(\frac { P }{ 2 }\) – x
Area of a rectangle ‘A’ = xy
A = x(\(\frac { P }{ 2 }\) – x) = \(\frac { P }{ 2 }\) x – x²
\(\frac { dA }{ dx }\) = \(\frac { P }{ 2 }\) – 2x
For maximum or minimum,
\(\frac { dA }{ dx }\) = 0 ⇒ \(\frac { P }{ 2 }\) – 2x = 0
x = \(\frac { P }{ 4 }\)
Now, \(\frac { d^2A }{ dx^2 }\) = -2
at x = \(\frac { P }{ 4 }\), \(\frac { d^2A }{ dx^2 }\) < 0
∴ Area of the rectangle is maximum when x = \(\frac { P }{ 4 }\)
Now, y = \(\frac { P }{ 2 }\) – x = \(\frac { P }{ 2 }\) – \(\frac { P }{ 4 }\) = \(\frac { P }{ 4 }\)
∴ Length of a rectangle = \(\frac { P }{ 4 }\)
Breadth of a rectangle = \(\frac { P }{ 4 }\)
Since Length = Breadth, the rectangle is a square.
Hence Proved.
Question 9.
Find the dimensions of the largest rectangle that can be inscribed in a semi-circle of radius r cm.
Solution:
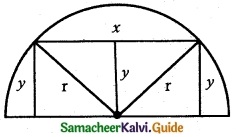
Given radius of the semi-circle = ‘r’ cm
Let the length of the rectangle be ‘x’ cm
Let the breadth of the rectangle be ‘y’ cm
From the figure,

For maximum or minimum,
\(\frac { dA }{ dx }\) = 0
⇒ \(\frac { 1 }{ 2 }\) [ \(\frac { 4r^2-2x^2 }{ \sqrt{4x^2-x^2} }\) ] = 0
4r² – 2x² = 0
x² = 2r²
x = ± √2 r
x = -√2 r is not possible
∴ x = √2 r
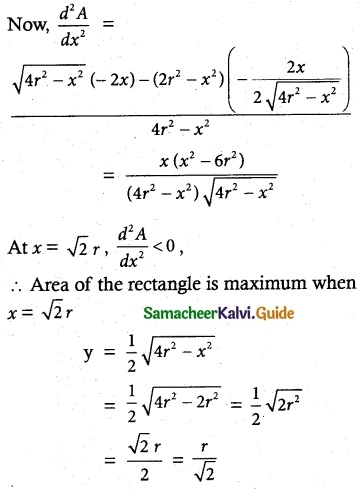
∴ Length of the rectangle is √2 r cm
Breadth of the rectangle is \(\frac { r }{ √2 }\) cm
![]()
Question 10.
A manufacturer wants to design an open box having a square base and a surface area of 108 sq. cm. Determine the dimensions of the box for the maximum volume.
Solution:
Let ‘x’ be the length Of the box.
‘y’ be the height of the box.
Given, surface area = 108 sq.cm
i,e. 4(xy) + x² = 108
⇒ y = \(\frac { 108-x^2 }{ 4x }\)
Volume of the box V = x²y
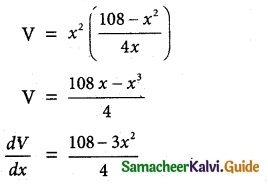
maximum or minimum, \(\frac { dV }{ dx }\) = 0
⇒ 108 – 3x² = 0
x² = 36
x = ± 6 [x = – 6 is not possible
∴ x = 6
Now, \(\frac { d^2V }{ dx^2 }\) = –\(\frac { 6x }{ 4 }\) = –\(\frac { 3x }{ 2 }\)
at x = 6, \(\frac { d^2V }{ dx^2 }\) < 0
Volume of theboxis maximum when x = 6
y = \(\frac { 108-36 }{ 24 }\) = \(\frac { 72 }{ 24 }\) = 3
∴ Length of the box = 6 cm
Breadth of the box = 6 cm
Height of the box = 3 cm
Question 11.
The volume of a cylinder is given by the formula V = πr²h. Find the greatest and least values of V if r + h = 6.
Solution:
Given r + h = 6
⇒ r = 6 – h
Volume V = πr²h
V = π(6 – h)²h
\(\frac { dV }{ dh }\) = π [(6 – h)² (1) + 2h(6 – h) (-1)] = π(6 – h)[6 – 3h]
For maximum or minimum,
\(\frac { dV }{ dh }\) = 0
⇒ π (6 – h) (6 – 3h) = 0
⇒ h = 6, h = 2
h = 6 is not possible as r + h = 6
∴ h = 2
\(\frac { d^2V }{ dh^2 }\) = π [(6 – h)(-3) + (6 – 3h)(-1)] = π [6h – 24]
at h = 2, \(\frac { d^2V }{ dh^2 }\) < 0
∴ Volume of the cylinder is maximum when h = 2 and r = 6 – 2 = 4
greatest value of V = π(4)² (2) = 32 π
least value of V = 0
![]()
Question 12.
A hollow cone with a base radius of a cm and’ height of b cm is placed on a table. Show that) the volume of the largest cylinder that can be hidden underneath is \(\frac { 4 }{ 9 }\) times the volume of the cone.
Solution:
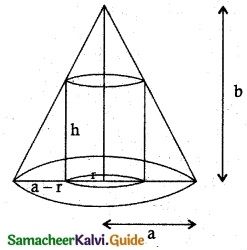
Cone
heigthof the cone = b cm
base radius = a cm
Cylinder
Let the base radius be ‘r’ cm
height be ‘h’ cm
From the figure, \(\frac { h }{ a-r }\) = \(\frac { b }{ a }\)
(using similar triangles property
⇒ h = \(\frac { b }{ a }\) (a – r)
= b – \(\frac { b }{ a }\) r
Volume of cylinder V = πr²h

For maximum or minimum,
\(\frac { dV }{ dr }\) = 0
⇒ br(2a – 3r) = 0
r = 0 and r = \(\frac { 2a }{ 3 }\)
r = 0 is not possible
∴ r = \(\frac { 2a }{ 3 }\)

Hence proved.
![]()