Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 Differentials and Partial Derivatives Ex 8.2 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.2
Question 1.
Find the differential dy for each of the following functions.
(i) y = \(\frac { (1-2x)^3 }{ 3-4x }\)
(ii) y = (3 + sin2x)2/3
(iii) y = ex2 – 5x +7 cos(x² – 1)
Solution:
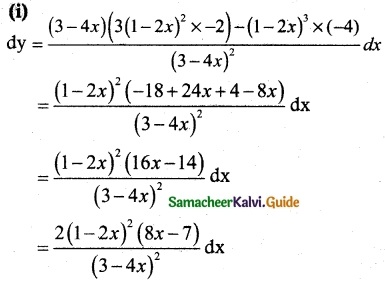
(ii) y = (3 + sin2x)2/3
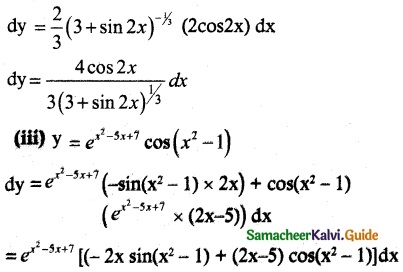
![]()
Question 2.
Find df for f(x) = x² + 3x and evaluate it for
(i) x = 2 and dx = 0.1
(ii) x = 3 and dx = 0.02
Solution:
y = f(x) = x2 + 3x
dy = (2x + 3) dx
(i) dy {when x = 2 and ate = 0.1} = [2(2) + 3] (0.1)
= 7(0.1) = 0.7
(ii) dy {when x = 3 and dx = 0.02} = [2(3) + 3] (0.0.2)
= 9(0.02) = 0.18
![]()
Question 3.
Find Δf and df for the function f for the indicated values of x, Δx and compare:
(i) f(x) = x³ – 2x², x = 2, Δx = dx = 0.5
(ii) f(x) = x² + 2x + 3, x = -0.5, Δx = dx = 0.1
Solution:
(i) y = f(x) = x3 – 2x2
dy = (3x2 – 4x) dx
dy (when x = 2 and dx = 0.5) = [3(22) – 4(2)] (0.5)
= (12 – 8)(0.5) = 4(0.5) = 2
(i.e.,) df = 2
Now ∆f = f(x + ∆x) – f(x)
Here x = 2 and ∆x = 0.5
f(x) = x3 – 2x2
So f(x + ∆x) = f(2 + 0.5) = f(2.5) = (2.5)3 – 2 (2.5)2 = (2.5)2 [2.5 – 2] = 6.25 (0.5) = 3.125
f(x) = f(2) = 23 – 2(22) = 8 – 8 = 0
So ∆f = 3.125 – 0 = 3.125
(ii) y = f(x) = x2 + 2x + 3
dy = (2x + 2) dx
dy (when x = – 0.5 and dx = 0.1)
= [2(-0.5) + 2] (0.1)
= (-1 + 2) (0.1) = (1) (0.1) = 0.1
(i.e.,) df = 0.1
Now ∆f = f(x + ∆x) – f(x)
Here x = -0.5 and ∆x = 0.1
x2 + 2x + 3
f(x + ∆x) = f(-0.5 + 0.1) = f(-0.4)
= (-0.4)2 + 2(-0.4) + 3
= 0.16 – 0.8 + 3 = 3.16 – 0.8 = 2.36
f(x) = f(-0.5) = (-0.5)2 + 2(-0.5) + 3
= 0.25 – 1 + 3 = 3.25 – 1 = 2.25
So ∆ f = f(x + ∆x) – f(x) = 2.36 – 2.25 = 0.11
![]()
Question 4.
Assuming log10 e = 0.4343, find an approximate value of Iog10 1003.
Solution:
Let f(x) = log 10 x then
f ‘(x) = \(\frac { 1 }{ x }\) log10 e (log10 x = log10 e loge x)
f(x + Δx) – f(x) = f ‘(x) Δx
f(1003) – f(1000) = \(\frac { 0.4344 }{ 1000 }\) × 3
log10 1003 – log10 1000 = 0.0013029
log10 1003 = log10 10³ + 0.0013029
= 3 + 0.0013029
= 3.0013029
Approximate value of log10 1003 = 3.0013029
Question 5.
The trunk of a tree has a diameter of 30 cm. During the following year, the circumference grew 6 cm.
(i) Approximately how much did the tree diameter grow?
(ii) What is the percentage increase in the area of the cross-section of the tree?
Solution:
(i) Diameter of the trunk of the tree
D = 30 cm
Rate of change of circumference
ds = 6 cm per year
Circumference S = πD
dS = πdD
6 = πdD
\(\frac { 6 }{ π }\) = dD
Rate of increasing diameter = \(\frac { 6 }{ π }\) cm

![]()
Question 6.
An egg of a particular bird is very nearly spherical. If the radius to the inside of the shell is 5 mm and the radius to the outside of the shell is 5.3 mm, find the volume of the shell approximately.
Solution:
Radius of the inside shell = 5 mm
Radius of the outside shell = 5.3 mm
Volume V = \(\frac { 4 }{ 3 }\) πr³
dV = \(\frac { 4 }{ 3 }\) π3r²dr
= 4 π 5 × 5 × 0.3
= 100 π × 0.3
= 30 π
Approximate volume of the shell = 30 mm³
Question 7.
Assume that the cross-section of the artery of human is circular. A drug is given to a patient to dilate his arteries. If the radius of an artery is increased from 2 mm to 2.1 mm, how much is the cross-sectional area increased approximately?
Solution:
The radius of an artery section = 2 mm
dr = 2.1 – 2
= 0.1
Area A = πr²
dA = 2πrdr
= 2 × π × 2 × 0.1
= 0.4 π
Increased area = 0.4 π mm²
![]()
Question 8.
In a newly developed city, it is estimated that the voting population (in thousands) will increase according to V(t) =30 + 12t² – t³, 0 ≤ t ≤ 8 where t is the time in years. Find the approximate change in voters for the time change from 4 to 4 1/6 years.
Solution:
V(t) = 30 + 12t² – t³; dt = 4 \(\frac { 1 }{ 6 }\) – 4 = \(\frac { 1 }{ 6 }\)
V’(t) = (24t – 3t²)dt
= (24(4)-3 (4)²) × \(\frac { 1 }{ 6 }\)
= (96 – 48) × \(\frac { 1 }{ 6 }\)
= 48 × \(\frac { 1 }{ 6 }\)
= 8
Voters in thousands
∴ Approximate change of voters = 8 × 1000 = 8000
Question 9.
The relation between the number of words y a person learns in x hours is given by y = 52√x, 0 ≤ x ≤ 9. What is the approximate number of words learned when x changes from
(i) 1 to 1.1 hours?
(ii) 4 to 4.1 hours?
Solution:
y = 52 √x
dy = 52 × \(\frac { 1 }{ 2 }\) × x-1/2 dx
x = 1, dx = 0.1
\(\frac { 26 }{ √x }\) × 0.1 = 26 × 0.1
= 2.6
≅ 3 words
(ii) y = 52 √y
dy = 52 × \(\frac { 1 }{ 2 }\) × x-1/2 dx
x = 4, dx = 0.1
\(\frac { 26 }{ √4 }\) × 0.1 = 13 × 0.1
= 1.3
≅ 1 word
![]()
Question 10.
A circular plate expands uniformly under the influence of heat. If its radius increases from 10.5 cm to 10.75 cm, then find an approximate change in the area and the approximate percentage change in the area.
Solution:
Area of the circular plate A = πr²
= π × 10.5 × 105
= 110.25 π
dA = 2πrdr
= 2π × 10.5 × 0.251
= 5.25 π
Approximate percentage change in the area
= \(\frac { dA }{ A }\) × 100
= \(\frac { 5.25π }{ 110.25π }\) × 100
= 0.04761 × 100
= 4.76%
Question 11.
A coat of paint of thickness 0.2 cm is applied to the faces of cube whose edge is 10 cm. Use the differentials to find approximately how many cubic centimeters of paint is used to paint this cube. Also calculate the exact amount of paint used to paint this cube.
Solution:
v = a3
so dv = a2 da
dv (when) a = 10 cm and da = 0.20 cm
= 3(102) (0.2)
300 × 0.2 = 60 cm3
Actual paint used = v at x + ∆x = 10.2 and x = 10 cm
= a3 at x + ∆x = 10.2 and x = 10
= (10.2)3 – (10) = 61.2 cm3
![]()