Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 Applications of Integration Ex 9.1 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.1
Question 1.
Find an approximate value of \(\int_{1}^{1.5}\) x dx by applying the left – end rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}
Solution:
Here a = 1, b = 1.5, n = 5, f(x) = x
So, the width of each subinterval is
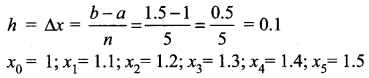
The left hand rule for Riemann sum,
S = [f(x0) + f(x1)) + f(x2) + f(x3) + f(x4)] ∆x
= [f(1) + f(1.1) + f(1.2) + f(1.3) + f(1.4)] (0.1)
= [1 + 1.1 + 1.2 + 1.3 + 1.4] (0.1)
= [6] (0.1)
= 0.6.
![]()
Question 2.
Find an approximate value of \(\int_{1}^{1.5}\) x² dx by applying the right – end rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}
Solution:
Here a = 1, b = 1.5, n = 5, f(x) = x²
So, the width of each subinterval is
h = Δx = \(\frac{b-a}{n}\) = \(\frac{1.5- 1}{5}\) = 0.1
The partition of the interval is given by
x1 = 1.1
x2 = 1.2
x3 = 1.3
x4 = 1.4
x5 = 1.5
The right – end rule for Riemann sum with equal width Δx is
S = [f(x1) + f(x2) + ….. + f(xn)] Δx
∴ S = [f(1.1) + f(1.2) + f(1.3) + f(1.4) + f(1.5)](0.1)
= (1.21 + 1.44 + 1.69 + 1.96 + 2.25) × 0.1
= 8.55 × 0.1
= 0.855
![]()
Question 3.
Find an approximate value of \(\int_{1}^{1.5}\) (2 – x) dx by applying the mid – point rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}
Solution:
Here a = 1, b = 1.5, n = 5, f(x) = 2 – x
So, the width of each subinterval is
h = Δx = \(\frac{b-a}{n}\) = \(\frac{1.5- 1}{5}\) = 0.1
The partition of the interval is given by
The partition of the interval is given b.y
x0 = 1, x1 = 1.1, x2=1.2, x3 = 1.3, x4 = 1.4, x5 = 1.5
The mid – point rule for Riemann sum with equal width Δx is

∴ S = (0.95 + 0.85 + 0.75 + 0.65 + 0.55) × 0.1
= 3.75 × 0.1
= 0.375
![]()