Samacheer Kalvi 12th Maths Guide Chapter 9 Applications of Integration Ex 9.10

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 Applications of Integration Ex 9.10 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.10

Choose the most suitable answer from the given four alternatives:

Question 1.
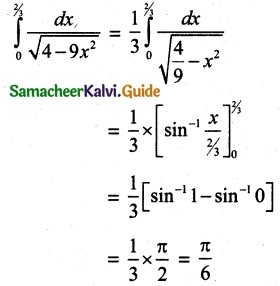
The value of \(\int_{0}^{2/3}\) \(\frac { dx }{ \sqrt{4-9x^2} }\)
(a) \(\frac { π }{ 6 }\)
(b) \(\frac { π }{ 2 }\)
(c) \(\frac { π }{ 4 }\)
(d) π
Solution:
(a) \(\frac { π }{ 6 }\)
Hint:

Question 2.
The value of \(\int_{-1}^{2}\) |x| dx
(a) \(\frac { 1 }{ 2 }\)
(b) \(\frac { 3 }{ 2 }\)
(c) \(\frac { 5 }{ 2 }\)
(d) \(\frac { 7 }{ 2 }\)
Solution:
(c) \(\frac { 5 }{ 2 }\)
Hint:
|x| = x if x > 0
= -x if x < 0

Question 3.
For any value of n ∈ Z \(\int_{0}^{π}\) e^cos²x cos3 [(2n + 1) x] dx
(a) \(\frac { π }{ 2 }\)
(b) π
(c) 0
(d) 2
Solution:
(c) 0
Hint:

Question 4.
The value of \(\int_{-π/2}^{π/2}\) sin² x cos x dx
(a) \(\frac { 3 }{ 2 }\)
(b) \(\frac { 1 }{ 2 }\)
(c) 0
(d) \(\frac { 2 }{ 3 }\)
Solution:
(d) \(\frac { 2 }{ 3 }\)
Hint:
f(x) = sin²x cos x
f(-x) = sin²(-x) cos(-x) = sin²x cos x
f(x) = f(-x)
f is an even function

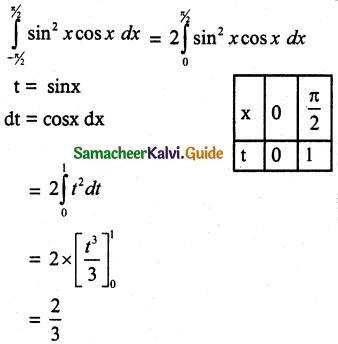
Question 5.
The value of \(\int_{-4}^{4}\)[tan^-1(\(\frac { x^2 }{ x^4+1 }\)) + tan^-1(\(\frac { x^4+1 }{ x^2 }\))] dx
(a) π
(b) 2π
(c) 3π
(d) 4π
Solution:
(d) 4π
Hint:

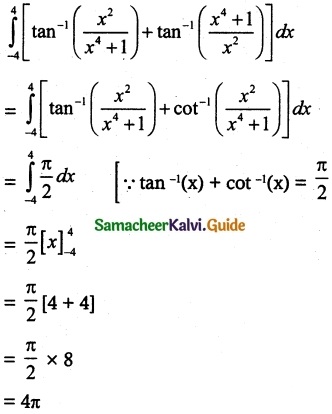
Question 6.
The value of \(\int_{-π/4}^{π/4}\) (\(\frac { 2x^7-3x^5+7x^3-x+1 }{ cos^2x }\)) dx is
(a) 4
(b) 3
(c) 2
(d) 0
Solution:
(c) 2
Hint:

Odd function – 3 Odd function + 7 Odd function – Odd function + even function
= 0 + 2 \(\int_{0}^{π/4}\) sec² x dx
= 2 [tan x]\(_{0}^{π/4}\)
= 2(1 – 0)
= 2

Question 7.
If f(x) = \(\int_{0}^{x}\) cos t dt, then \(\frac { df }{ dx }\) =
(a) cos x – x sin x
(b) sin x + x cos x
(c) x cos x
(d) x sin x
Solution:
(c) x cos x
Hint:
f(x) = \(\int_{0}^{x}\) cos t dt
u = t, dv = cos t dt
u’ = 1, v = sin t
v₁ = -cos t
f(x) = [t sin t + cos t]\(_{0}^{x}\)
f(x) = x sin x + cos x – 1
\(\frac { df }{ dx }\) = x cos + sin x – sin x
\(\frac { df }{ dx }\) = x cos x

Question 8.
The area between y² = 4x and its latus rectum is
(a) \(\frac { 2 }{ 3 }\)
(b) \(\frac { 4 }{ 3 }\)
(c) \(\frac { 8 }{ 3 }\)
(d) \(\frac { 5 }{ 3 }\)
Solution:
(c) \(\frac { 8 }{ 3 }\)
Hint:
y² = 4x
y = 2√x

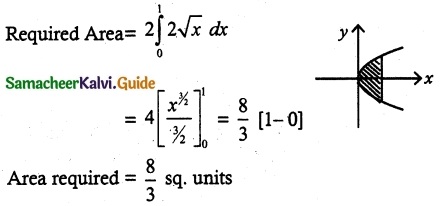
Question 9.
The value of \(\int_{0}^{1}\) x (1 – x)⁹⁹ dx is
(a) \(\frac { 1 }{ 11000 }\)
(b) \(\frac { 1 }{ 10100}\)
(c) \(\frac { 1 }{ 10010 }\)
(d) \(\frac { 1 }{ 10001 }\)
Solution:
(b) \(\frac { 1 }{ 10100}\)
Hint:

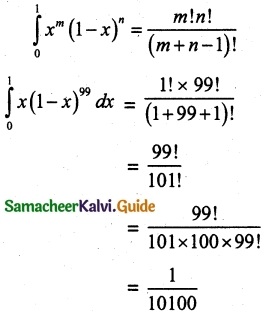
Question 10.
The value of \(\int_{0}^{π}\) \(\frac { dx }{ 1+5^{cosx} }\) is
(a) \(\frac { π }{ 2 }\)
(b) π
(c) \(\frac { 3π }{ 2 }\)
(d) 2π
Solution:
(a) \(\frac { π }{ 2 }\)
Hint:

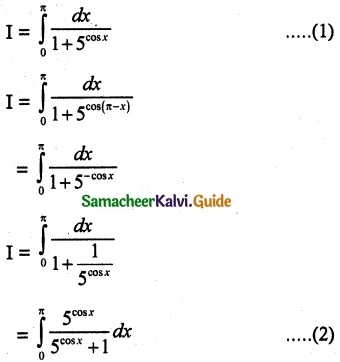
Adding (1) and (2)

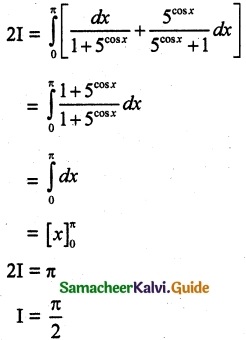
Question 11.
If \(\frac { Γ(n+2) }{ Γn }\) = 90 then n is
(a) 10
(b) 5
(c) 8
(d) 9
Solution:
(d) 9
Hint:

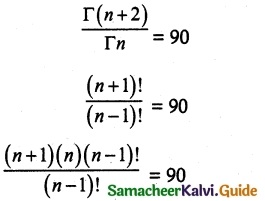
n² + n = 90
n² + n – 90 = 0
(n + 10) (n – 9) = 0
n = 9

Question 12.
The value of \(\int_{0}^{π/6}\) cos³ 3x dx is
(a) \(\frac { 2 }{ 3 }\)
(b) \(\frac { 2 }{ 9}\)
(c) \(\frac { 1 }{ 9 }\)
(d) \(\frac { 1 }{ 3 }\)
Solution:
(b) \(\frac { 1 }{ 10100}\)
Hint:
\(\int_{0}^{π/6}\) cos³ 3xdx = \(\frac { 1 }{ 3 }\) × \(\frac { 2 }{ 3 }\) × 1
= \(\frac { 2 }{ 9 }\)

Question 13.
The value of \(\int_{0}^{π}\) sin⁴ x dx
(a) \(\frac { 3π }{ 10 }\)
(b) \(\frac { 3π }{ 8}\)
(c) \(\frac { 3π }{ 4 }\)
(d) \(\frac { 3π }{ 2 }\)
Solution:
(b) \(\frac { 3π }{ 8}\)
Hint:
(x) = sin⁴x dx
f(π – x) = sin⁴ (π – x) = sin⁴x

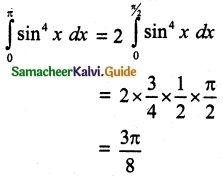
Question 14.
The value of \(\int_{0}^{∞}\) e^-3x x² dx
(a) \(\frac { 7 }{ 27 }\)
(b) \(\frac { 5 }{ 27 }\)
(c) \(\frac { 4 }{ 27 }\)
(d) \(\frac { 2 }{ 27 }\)
Solution:
(d) \(\frac { 2 }{ 27 }\)
Hint:

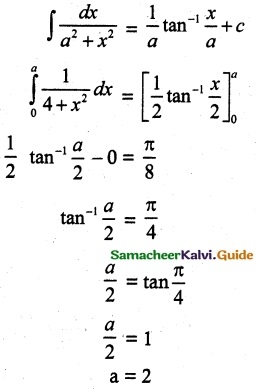
Question 15.
If \(\int_{0}^{a}\) \(\frac { 1 }{ 4+x^2 }\) dx = \(\frac { π }{ 8 }\) then a is
(a) 4
(b) 1
(c) 3
(d) 2
Solution:
(d) 2
Hint:

Question 16.
The volume of solid of revolution of the region bounded by y² = x(a – x) about the x-axis is
(a) πa³
(b) \(\frac { πa^3 }{ 4 }\)
(c) \(\frac { πa^3 }{ 5 }\)
(d) \(\frac { πa^3 }{ 6 }\)
Solution:
(d) \(\frac { πa^3 }{ 6 }\)
Hint:
y² = x(a – x)
To find limit put y = 0
x (a – x) = 0
x = 0, x = a

Question 17.
If f(x) = \(\int_{1}^{x}\) \(\frac { e^{sinx} }{ u }\) du, x > 1 and \(\int_{1}^{3}\) \(\frac { e^{sinx^2} }{ x }\) dx = \(\frac { πa^3 }{ 6 }\) [f(a) – f(1)] then one of the possible value of a is
(a) 3
(b) 6
(c) 9
(d) 5
Solution:
(c) 9
Hint:

Question 18.
The value of \(\int_{0}^{1}\) (sin^-1 x)² dx is
(a) \(\frac { π^2 }{ 4 }\) – 1
(b) \(\frac { π^2 }{ 4 }\) + 2
(c) \(\frac { π^2 }{ 4 }\) + 1
(d) \(\frac { π^2 }{ 4 }\) – 2
Solution:
(d) \(\frac { π^2 }{ 4 }\) – 2
Hint:

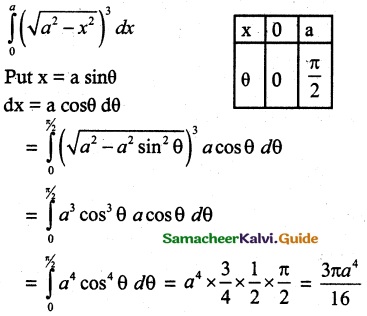
Question 19.
The value of \(\int_{0}^{a}\) (\(\sqrt{a^2-x^2}\))³ dx is
(a) \(\frac { πa^3 }{ 16 }\)
(b) \(\frac { 3πa^4 }{ 16 }\)
(c) \(\frac { 3πa^2 }{ 8 }\)
(d) \(\frac { 3πa^4 }{ 8 }\)
Solution:
(b) \(\frac { 3πa^4 }{ 16 }\)
Hint:

Question 20.
If \(\int_{0}^{x}\) f(t) dt = x + \(\int_{x}^{1}\) f(t) dt, then the value of f(1) is
(a) \(\frac { 1 }{ 2 }\)
(b) 2
(c) 1
(d) \(\frac { 3 }{ 4 }\)
Solution:
(a) \(\frac { 1 }{ 2 }\)
Hint:

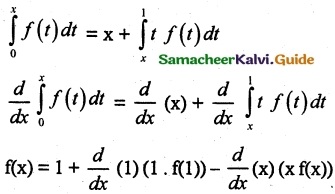
= 1 + 0 – x f(x)
f(x) + x f(x) = 1
f(x)[1 + x] = 1
when x = 1,
f(1)(2) = 1
f(1) = \(\frac { 1 }{ 2 }\)