Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 Applications of Integration Ex 9.8 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.8
Question 1.
Find the area of the region bounded by 3x – 2y + 6 = 0, x = -3, x = 1 and x axis.
Solution:
3x – 2y + 6 = 0
2y = 3x + 6
y = \(\frac { 1 }{ 2 }\)(3x + 6)

![]()
Question 2.
Find the area of the region bounded by 2x – y + 1 = 0, y = -1, y = 3 and y axis.
Solution:
Given straight line is 2x – y + 1 = 0
y = 2x + 1, x = \(\frac { y-1 }{ 2 }\)
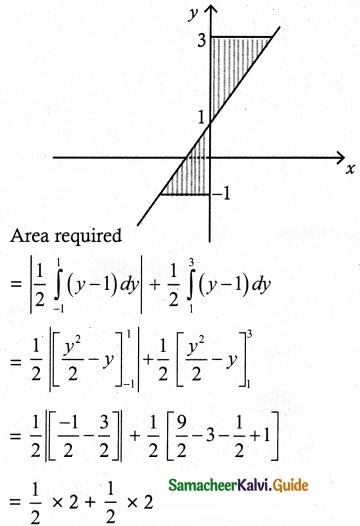
= 1 + 1
= 2 sq. units
Area required = 2 sq. units
Question 3.
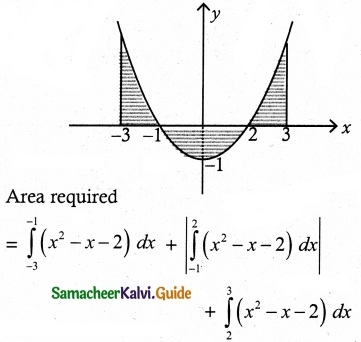
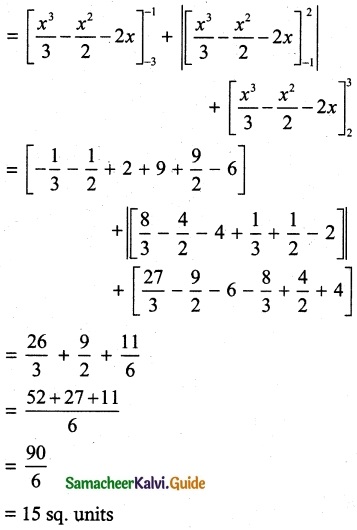
Find the area of the region bounded by the curve 2 + x – x² + y = 0, x axis, x = -3 and x = 3
Solution:
Given curve is
2 + x – x² + y = 0
y = x² – x – 2
y = (x – 2)(x + 1)
![]()
Question 4.
Find the area of the region bounded by the line y = 2x + 5 and the parabola y = x² – 2x.
Solution:
First, we find the point of intersection of
y = 2x + 5 and y = x² – 2x
x² – 2x = 2x + 5
x² – 4x – 5 = 0
(x – 5) (x + 1) = 0
x = 5, x = – 1
when x = 5, y = 15
x = -1. y = 3
(5, 15) (-1, 3) are intersecting points.
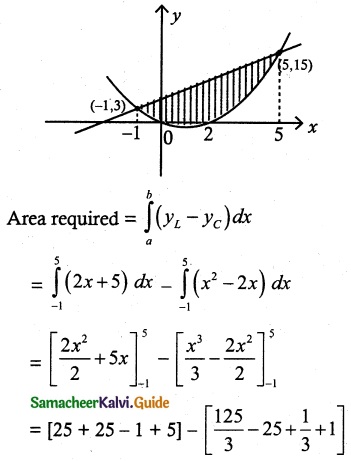
54 – 18 = 36
Area required = 36 sq. units
Question 5.
Find the area of the region bounded between the curves y = sin x and y = cos x and the lines x = 0 and x = π
Solution:
First find the intersecting point of two curves
sin x = cos x
tan x = 1
x = \(\frac { π }{ 4 }\)
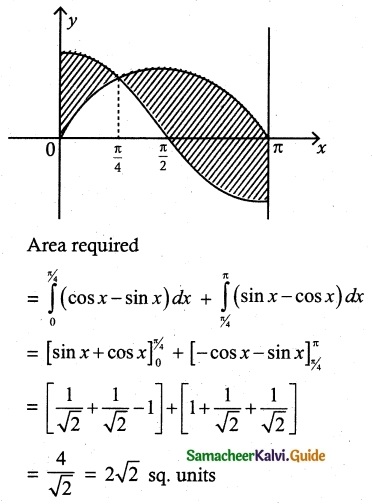
Area required = 2√2 sq. units
![]()
Question 6.
Find the area of the region bounded by y = tan x, y = cot x and the lines x = 0, x = \(\frac { π }{ 2}\), y = 0.
Solution:
First find the intersecting point of y = tan x and y = cot x
tan x = cot x
\(\frac { tan x }{ cot x }\) = 1
tan²x = 1
tan x = 1
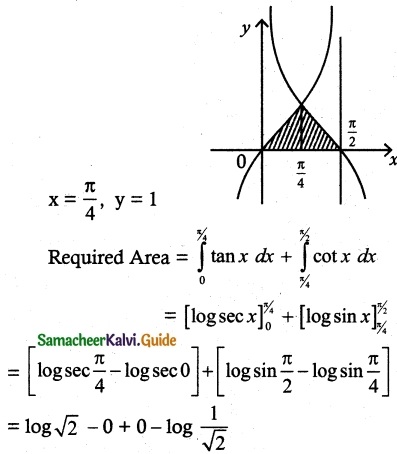
= log √2 + log √2
= 2 log √2
= log(√2)²
= log 2 sq. units
![]()
Question 7.
Find the area of the region bounded by the parabola y² = x and the line y = x – 2.
Solution:
First find the intersecting point of y² = x and y = x – 2
y = y² – 2
y² – y – 2 = 0
y = 2, y = -1
Intersecting points are (4, 2), (1, -1)
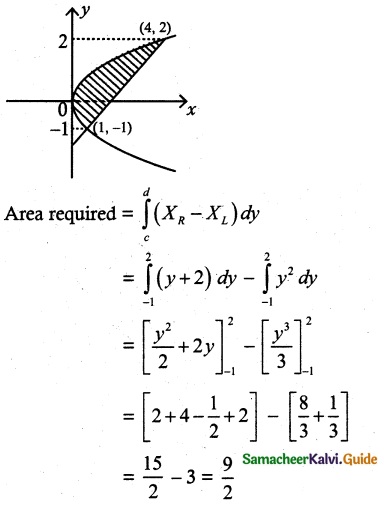
Required Area = \(\frac { 9 }{ 2 }\) sq. units
![]()
Question 8.
Father of a family wishes to divide his square field bounded by x = 0, x = 4, y = 4 and y = 0 along the curve y² = 4x and x² = 4y into three equal parts for his wife, daughter and son. Is it possible to divide? If so, find the area to be divided among them.
Solution:
Given curve y² = 4x and x² = 4y
Draw these two curves
Also draw the square bounded by the lines
x = 0, x = 4, y = 4 and y = 0
To prove Area A1 = Area A2 = Area A3
Now the point of intersection of the curves y² = 4x and x² = 4y is given by
(\(\frac { y^2 }{ 4 }\))² = 4y
y4 = 64y ⇒ y (y³ – 64) = 0
y = 0, y = 4
when y = 0 ⇒ x = 0
y = 4 ⇒ x = 4
Point of intersection are O (0, 0) and B (4, 4)
Now, the area of the region bounded by the curves y² = 4x and x² = 4y is
A2 = \(\int_{0}^{4}\)(\(\sqrt { 4x }\) – \(\frac { x^2 }{ 4 }\)) dx
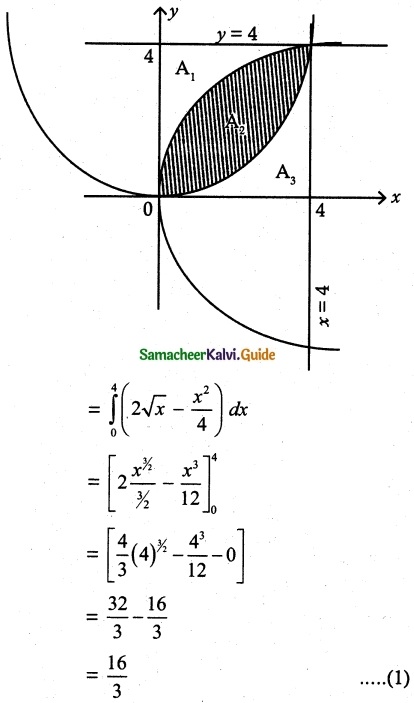
Now the area of the region bounded by the curves x² = 4y, x = 4 and x axis is

Similarly the area of the region bounded by the curve y² = 4x, y axis and y = 4 is

Hence we see that
A1 = A2 = A3 = \(\frac { 16 }{ 3 }\) sq. units
![]()
Question 9.
The curve y = (x – 2)² + 1 has a minimum point at P. A point Q on the curve is such that the slope of PQ is 2. Find the area bounded by the curve and the chord PQ.
Solution:
Given curve is y = (x – 2)² + 1
(i.e) (y – 1) = (x – 2)²
Vertex of the parabola is (2, 1)
Minimum point P is (2, 1)
Slope of PQ is 2.
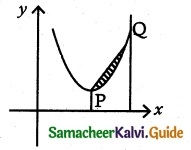
Equation of PQ is y – 1 = 2 (x – 2)
y – 1 = 2x – 4
y = 2x – 3
Intersecting point of y = 2x – 3 and y = (x – 2)² + 1
2x – 3 = (x – 2)² + 1
2x – 4 = (x – 2)²
2(x – 2) = (x – 2)²
x – 2 = 2
x = 4
when x = 4, y = 5

Required Area = \(\frac { 4 }{ 3 }\) sq. units
![]()
Question 10.
Find the area of the region common to the circle x² + y² = 16 and the parabola y² = 6x
Solution:
First find the intersecting point of the curves
x² + y² = 16 and y² = 6x
x² + 6x = 16
x² + 6x – 16 = 0
(x + 8) (x – 2) = 0
x = -8, x = 2
x = -8 is impossible
x = 2, y = 2√3
Radius of the circle x² + y² = 16 is 4
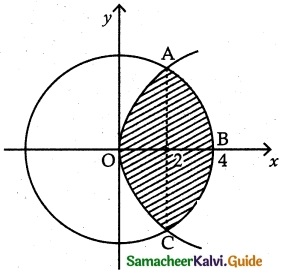
Area OABC = 2 (Area of OAB)
= 2 (Area of the curve y² = 6x in [0, 2] + Area of the curve x² + y² = 16 in [2, 4])

Required Area = \(\frac { 4 }{ 3 }\) [4π + √3] sq. units
![]()