Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 Applications of Integration Ex 9.9 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.9
Question 1.
Find by integration, the volume of the solid generated by revolving about the x axis, the region enclosed by y = 2x², y = 0 and x = 1
Solution:
The region to be revolved is sketched
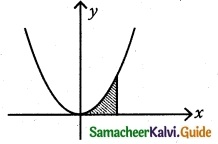
Since revolution is made about the x axis, the volume of the solid generated is given by
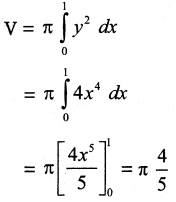
Required volume = \(\frac { 4π }{ 5 }\) cubic units
![]()
Question 2.
Find, by integration, the volume of the solid generated by revolving about the x axis, the region enclosed by y = e-2x, y = 0, x = 0 and x = 1.
Solution:
Since revolution is made about the x axis, the volume of the solid generated is given
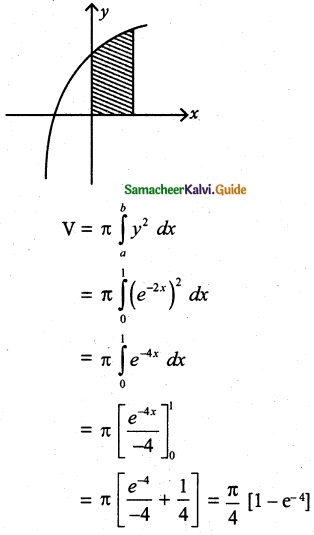
Required volume = \(\frac { π }{ 4 }\) [1 – e-4] cubic units
![]()
Question 3.
Find, by integration, the volume of the solid generated by revolving about the y axis, the region enclosed by x² = 1 + y and y = 3.
Solution:
The region to be revolved is sketched.
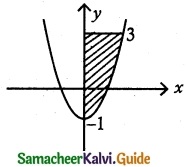
Since revolution is made about the y axis, the volume of the solid generated is given by
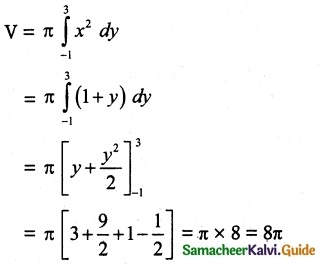
Required volume = 8π cubic units
![]()
Question 4.
The region enclosed between the graphs of y = x and y = x² is denoted by R. Find the volume generated when R is rotated through 360° about x axis.
Solution:
The region to be revolved is sketched.
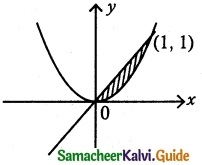
Find the intersecting point of y = x and y = x²
x² = x
x² – x = 0
x (x – 1) = 0 x = 0, x = 1
If x = 0, y = 0, x = 1, y = 1
∴ Points of intersection are (0, 0), (1, 1)
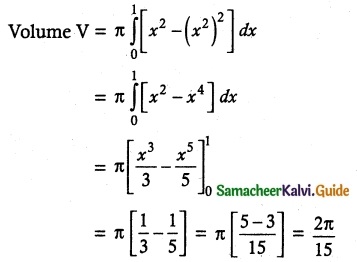
Required volume = \(\frac { 2π }{ 15 }\) cubic units
![]()
Question 5.
Find, by integration, the volume of the container which is in the shape of a right circular conical frustum as shown to figure.
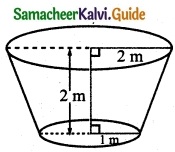
Solution:
By using integration we have to find the volume of the frustum. So first find the equation of the curve.
Let A(0, 1) and B(2, 2) be two points. Line joining these two points form a straight line. That straight line revolves around x axis.
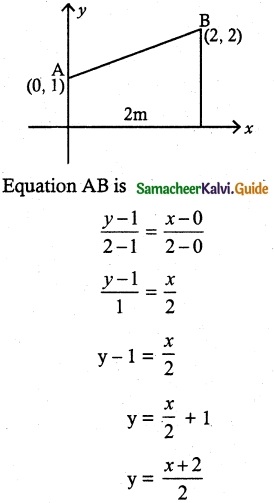
Volume of the solid revolves around x axis
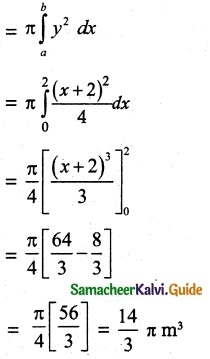
Volume of the frustum = \(\frac { 14 }{ 3 }\) π m³
![]()
Question 6.
A watermelon has an ellipsoid shape which can be obtained by revolving an ellipse with major axis 20 cm and minor axis 10 cm about its major axis. Find its volume using integration.
Solution:
A watermelon has an ellipsoid shape.
2a = 20
a = 10
2b = 10
b = 5

∴ Volume of the frustum = \(\frac { 1000π }{ 3 }\) cubic units.
![]()