Samacheer Kalvi 12th Physics Guide Chapter 3 Magnetism and Magnetic Effects of Electric Current

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Physics Guide Pdf Chapter 3 Magnetism and Magnetic Effects of Electric Current Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 3 Magnetism and Magnetic Effects of Electric Current

12th Physics Guide Magnetism and Magnetic Effects of Electric Current Text Book Back Questions and Answers

Part – 1

Text Book Evaluation:

I. Multiple choice questions:

Question 1.
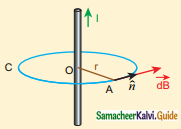
The magnetic field at the center O of the following current loop is

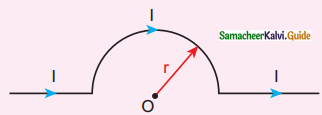
a) \(\frac{\mu_{0} I}{4 r} \otimes\)
b) \(\frac{\mu_{\mathrm{o}} \mathrm{I}}{4 \mathrm{r}} \odot\)
c) \(\frac{\mu_{\mathrm{o}} \mathrm{I}}{2 \mathrm{r}} \otimes\)
d) \(\frac{\mu_{\mathrm{o}} \mathrm{I}}{2 \mathrm{r}} \odot\)
Answer:
a) \(\frac{\mu_{0} I}{4 r} \otimes\)
Solution:

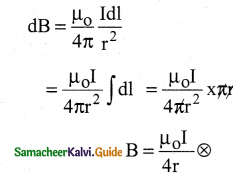
Question 2.
An electron moves straight line inside a charged parallel plate capacitor of uniform charge density σ. The time taken by the electron to cross the parallel plate capacitor undeflected when the plates of the capacitor are kept under constant magnetic field of induction B is

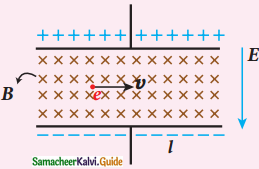
a) \(\varepsilon_{0} \frac{\mathrm{elB}}{\sigma}\)
b) \(\varepsilon_{\mathrm{O}} \frac{\mathrm{lB}}{\sigma l}\)
c) \(\varepsilon_{\mathrm{o}} \frac{\mathrm{lB}}{\mathrm{e} \sigma}\)
d) \(\varepsilon_{0} \frac{\mathrm{B}}{\sigma}\)
Answer:
\(\varepsilon_{0} \frac{\mathrm{B}}{\sigma}\)
Solution:
\(\mathrm{E}=\frac{\sigma}{\varepsilon_{\mathrm{o}}}\)
[∴Parallel plate capacitors]

Question 3.
A particle having mass m and charge q accelerated through a potential difference V. Find the force experienced when it is kept under perpendicular magnetic field B is
a) \(\sqrt{\frac{2 q^{3} B V}{m}}\)
b) \(\sqrt{\frac{q^{3} B^{2} V}{2 m}}\)
c) \(\sqrt{\frac{2 q^{3} B^{2} V}{m}}\)
d) \(\sqrt{\frac{2 q^{3} B V}{m^{3}}}\)
Answer:
\(\sqrt{\frac{2 q^{3} B^{2} V}{m}}\)
Solution:

Question 4.
A circular coil of radius 5 cm arid has 50 turns carries a current of 3 amperes. The magnetic dipole moment of the coil is
a) 1.0 Am²
b) 1.2 Am²
c) 0.5 Am²
d) 0.8 Am²
Answer:
b) 1.2 Am²
Solution:
r = 5 cm = 5 × 10^-2m
N = 50 turns
I = 3A
M = NIA = 50 × 3 × 3.14 × 25 × 104
M = 1.2amp – m²

Question 5.
A thin insulated wire forms a plane spiral of N=100 tight turns carrying a current I = 8mA (milliampere). The radii of inside and outside turns are a = 50mm and b = 100 mm, respectively. The magnetic induction at the center of the spiral is
a) 5 µT
b) 7 µT
c) 8 µT
d) 10 µT
Answer:
b) 7 µT
Solution:

Question 6.
Three wires of equal lengths are bent in the form of loops. One of the loops is a circle, another is a semi-circle and the third one is a square. They are placed in a uniform magnetic field and the same electric current is passed through them. Which of the following loop configuration will experience greater torque?
a) circle
b) semi-circle
c) square
d) all of them
Answer:
a) Circle
Solution:
Circle has greater torque because torque is directly proportional to area.

Question 7.
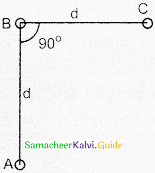
Two identical coils, each with N turns and radius R are placed coaxially at a distance R as shown in the figure. If I is the current passing through the loops in the same direction, then the magnetic field at a point P at a distance of R/2 from the center of each coil

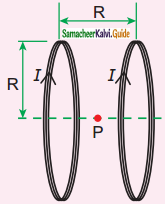
a) \(\frac{8 \mathrm{~N} \mu_{\mathrm{o}} \mathrm{I}}{\sqrt{5} \mathrm{R}}\)
b) \(\frac{8 \mathrm{~N} \mu_{\mathrm{o}} \mathrm{I}}{5^{3 / 2} \mathrm{R}}\)
c) \(\frac{8 \mathrm{~N} \mu_{\mathrm{O}} \mathrm{I}}{5 \mathrm{R}}\)
d) \(\frac{4 \mathrm{~N} \mu_{\mathrm{o}} \mathrm{I}}{\sqrt{5} \mathrm{R}}\)
Answer:
b) \(\frac{8 \mathrm{~N} \mu_{\mathrm{o}} \mathrm{I}}{5^{3 / 2} \mathrm{R}}\)
Solution:

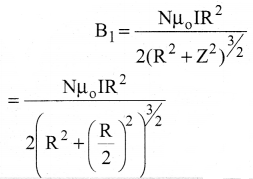
Question 8.
A wire of length l carrying a current I along the Y direction is kept in a and magnetic field is given by
\(\mathrm{B}=\frac{\beta}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k}) T\).
The magnitude of Lorentz force acting on the wire is
a) \(\sqrt{\frac{2}{\sqrt{3}}} \beta \mathrm{I} l\)
b) \(\sqrt{\frac{1}{\sqrt{3}}} \beta I l\)
c) √2βIl
d) \(\sqrt{\frac{1}{2}} \beta \mathrm{I} l\)
Answer:
a) \(\sqrt{\frac{2}{\sqrt{3}}} \beta \mathrm{I} l\)
Solution:

Question 9.
A bar magnet of length l and magnetic moment p_m is bent in the form of an arc as shown in Figure. The new magnetic dipole moment will be

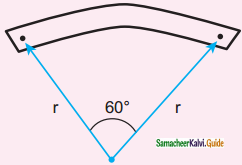
a) p_m
b) \(\frac{3}{\pi} p_{m}\)
c) \(\frac{2}{\pi} \mathrm{p}_{\mathrm{m}}\)
d) \(\frac{1}{2} \mathrm{p}_{\mathrm{m}}\)
Answer:
b) \(\frac{3}{\pi} p_{m}\)
Solution:

Question 10.
A non-conducting charged ring of charge of q, mass m and radius r is rotated about its axis with constant angular speed to. Find the ratio of its magnetic moment with angular momentum is
a) \(\frac{q}{m}\)
b) \(\frac{2 q}{m}\)
c) \(\frac{\mathrm{q}}{2 \mathrm{~m}}\)
d) \(\frac{q}{4 m}\)
Answer:
c) \(\frac{\mathrm{q}}{2 \mathrm{~m}}\)
Solution:

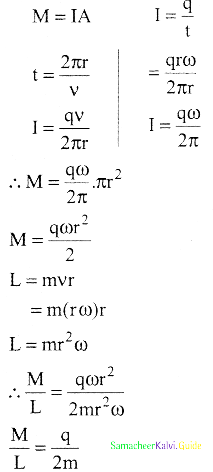
Question 11.
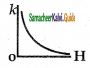
The BH curve for a ferromagnetic material is shown in the Figure. The material is placed inside a long solenoid which contains 1000 turns/cm. The current that should be passed in the solenoid to demagnetize the ferromagnet completely is

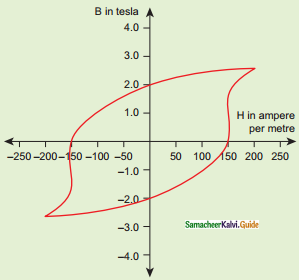
a) 1.00 mA
b) 1.25 mA
c) 1.50 mA
d) 1.75 mA
Answer:
c) 1.50 mA

Question 12.
Two short bar magnets have magnetic moments 1.20 Am² and 1.00 Am², respectively. They are kept on a horizontal table parallel to each other with their north poles pointing towards the south. They have a common magnetic equator and are separated by a distance of 20.0 cm. The value of the resultant horizontal magnetic induction at the mid¬point O of the line joining their centers is (Horizontal components of Earth’s magnetic induction is 3.6 × 10^-5 Wbm^-2)
a) 3.60 × 10^-5 Wbm^-2
b) 3.5 × 10^-5 Wbm^-2
c) 2.56 × 10^-4 Wbm^-2
d) 2.2 × 10^-4 Wbm^-2
Answer:
c) 2.56 × 104^-5 Wbm²
Solution:
\(B=\frac{\mu_{0}}{4 \pi} \frac{M}{\left(d^{2}+L^{2}\right)^{3 / 2}}\)
M₁ = 1.2 Am²
M₂ = 1 Am²
2L = 0.01m, 2d = 0.2m
\(B_{1}=\frac{4 \pi x 10^{-7} \times 1.2}{4 \pi\left[(0.1)^{2}+(0.005)^{2}\right]^{3 / 2}}\)
B₁ = 1.1955 × 10^-4 Wbm^-2
\(\mathrm{B}_{2}=\frac{4 \pi \times 10^{-7} \times 1}{4 \pi\left[(0.10)^{2}+(0.005)^{2}\right]^{3 / 2}}\)
B₂ = 1.1963 × 10^-4 Wbm^-2
B = B₁ + B₂ + B_earth
= (1.1955 + 1.1963 + 0.36) × 10^-4
B = 2.56 × 10^-4 Wbm^-2

Question 13.
The vertical component of Earth’s magnetic field at a place is equal to the horizontal component. What is the value of the angle of dip at this place?
a) 30°
b) 45°
c) 60°
d) 90°
Answer:
b) 45°
Solution:
B_H = B_E cos I
B_V = B_E sin I
B_E cos I = B_E sin I
\(\frac{\sin I}{\cos I}=1\)
tan I = 1
I = 45°

Question 14.
A flat dielectric disc of radius R carries an excess charge on its surface. The surface charge density is σ. The disc rotates about an axis perpendicular to its plane passing through the center with angular velocity ω. Find the magnitude of the torque on the disc if it is placed in a uniform magnetic field whose strength is B which is directed perpendicular to the axis of rotation
a) \(\frac{1}{4}\)σωπBR
b) \(\frac{1}{4}\)σωπBR²
c) \(\frac{1}{4}\)σωπBR³
d) \(\frac{1}{4}\)σωπBR⁴
Answer:
d) \(\frac{1}{4}\)σωπBR⁴
Solution:

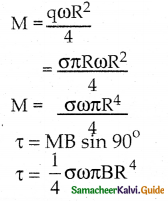
Question 15.
The potential energy òf magnetic dipole whose dipole moment is \(\vec{p}_{m}=(-0.5 \hat{i}+0.4 \hat{j}) \mathrm{Am}^{2}\) Am² kept in uniform magnetic field \(\vec{B}=0.2 \hat{i} \mathrm{~T}\)
a -0.1 J
b) -0.8 J
c) 0.1 J
d) 0.8 J
Answer:
c) 0.1 J

II. Short Answer Questions:

Question 1.
What is meant by magnetic induction?
Answer:
The magnetic induction (total magnetic field) inside the specimen \(\vec { B } \) is equal to the sum of the magnetic field \(\vec { B } \)₀ produced in vacuum due to the magnetising field and the magnetic field \(\vec { B } \)_m due to the induced magnetisation of the substance.
\(\vec { B } \) = \(\vec { B } \)₀ + \(\vec { B } \)_m = µ₀\(\vec { H } \) + µ₀\(\vec { I } \) = µ₀ (\(\vec { H } \) + \(\vec { I } \)) = (\(\vec { H } \) + \(\vec { I } \))

Question 2.
Define magnetic flux.
Answer:

1. The number of magnetic field lines crossing per unit area.
2. φ_B = \(\overrightarrow{\mathrm{B}}\) . \(\overrightarrow{\mathrm{A}}\) = BA cos θ
3. S.I unit: weber (Wb); Dimensional formula [ML²T^-2A^-1]

Question 3.
Define magnetic dipole moment.
Answer:
The magnetic dipole moment is defined as the product of its pole strength and magnetic length.
\(\vec { P } \) = q_m \(\vec { d } \)

Question 4.
State Coulomb’s inverse law.
Answer:
The force of attraction or repulsion between two magnetic poles is directly proportional to the product of their pole strengths and inversely proportional to the square of distance between them,
\(\overrightarrow{\mathrm{F}} \alpha \frac{\mathrm{q}_{\mathrm{m}_{\mathrm{A}}} \mathrm{q}_{\mathrm{m}_{\mathrm{B}}}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\) ;
\(\mathrm{F}=\frac{\mathrm{K} \mathrm{q}_{\mathrm{m}} \mathrm{A} \quad \mathrm{q}_{\mathrm{m}} \mathrm{B}}{\mathrm{r}^{2}}\)
q_mA & q_mB – pole strengths of two poles,
r – distance between two magnetic poles.

Question 5.
What is magnetic susceptibility?
Answer:
It is defined as the ratio of the intensity of magnetisation (\(\vec { M } \)) induced in the material due to the magnetising field (\(\vec { H } \))
\(\chi_{m}=\left|\frac{\overrightarrow{\mathrm{M}}}{\overrightarrow{\mathrm{H}}}\right|\)

Question 6.
State Biot-Savart’s law.
Answer:
The magnitude of magnetic field d\(\overrightarrow{\mathrm{B}\) at a point P at a distance r from the small length on a current-carrying conductor varies,
i) directly as the strength of the current I
ii) directly as the magnitude of the length element dI and r
iii) directly as the sine of the angle between dI and r̂
iv) inversely as the square of the distance between the point P and length element dl

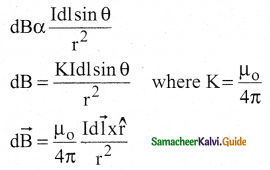
Question 7.
What is magnetic permeability?
Answer:
Magnetic permeability: Magnetic permeability can be defined as the measure of the ability of the material to allow the passage of magnetic field lines through it or a measure of the capacity of the substance to take magnetisation or the degree of penetration of the magnetic field through the substance.

Question 8.
State Ampere’s circuital law.
Answer:
The line integral of magnetic field over a closed loop is μ₀ times net current enclosed by loop.
\(\oint_{C} \vec{B} \cdot \vec{l}=\mu_{o} I_{\text {enclosed }}\)
I_enclosed → net current in the closed loop C.

Question 9.
Compare dia, para and ferro-magnetism.
Answer:

Diamagnetism	Paramagnetism	Ferro magnetism
A force tends to move the material from the stronger part to the weaker part of the external field.	Weak magnetism in the direction of the applied field.	Strong magnetism in the direction of the applied field.
Each electron has finite orbital magnetic dipole moments.	Each atom has a net magnetic dipole moment.	Have net dipole moment as in a paramagnetic material.
Since the orbital planes are oriented in a random manner, the vector sum of magnetic moments is zero.	Due to the random orientation of the magnetic moments, the net magnetic moment of the material is zero.	Within each domain, the magnetic moments are spontaneously aligned in a direction.
The resultant magnetic moment for each atom is zero.	There is a net magnetic dipole moment induced in the direction of the applied field.	Since the direction of magnetisation varies from domain to domain, the net magnetisation of the specimen is zero.

Question 10.
What is meant by hysteresis?
Answer:
The phenomenon of lagging of magnetic induction behind the magnetising field is called hysteresis. Hysteresis means Tagging behind’.

Question 11.
Define magnetic declination and inclination?
Answer:
Magnetic declination:

1. The angle between magnetic meridian at a point and geographical meridian.
2. Higher altitude – Greater declination
3. Equator – Smaller declination.
4. Magnetic inclination: The angle subtended by the Earth’s total magnetic field \(\overrightarrow{\mathrm{B}}\) with the horizontal direction in the magnetic meridian.

Question 12.
What is the resonance condition in a cyclotron?
Answer:

1. In cyclotron operation when the frequency f at which the positive ion circulates in the magnetic field must be equal to the constant frequency of the electrical oscillator f_osc. This is called resonance condition.
   f_osc = \(\frac{q B}{2 \pi m}\)
2. The time period of oscillation is T = \(\frac{2 \pi \mathrm{m}}{\mathrm{qB}}\)
3. The kinetic energy of charged particle is \(\mathrm{KE}=\frac{1}{2} \mathrm{mv}^{2}=\frac{\mathrm{q}^{2} \mathrm{~B}^{2} \mathrm{r}^{2}}{2 \mathrm{~m}}\)

Question 13.
Define ampere.
Answer:
Current passed through each of the two infinitely long parallel straight conductors kept at a distance of one meter apart in vacuum causes each conductor to experience a force of 2 × 10^-7 newton per meter length of the conductor.

Question 14.
State Fleming’s left-Hand rule.
Answer:

1. Stretch forefinger, the middle finger, and the thumb of the left hand such that they are in mutually perpendicular directions.
2. The forefinger points the direction of the magnetic field.
3. The middle finger points in the direction of the electric current.
4. Thumb will point the direction of the force experienced by the conductor.

Question 15.
Is an ammeter connected in series or parallel in a circuit? Why.
Answer:

1. An ammeter is a low resistance instrument and it is always connected in series to the circuit.
2. Such that it will change the current passing through it.

Question 16.
Explain the concept of the selector.
Answer:

1. For a given magnitude of E field and B field, the forces act only on the particle moving with particular speed p.
   \(v=\frac{E}{B}\)
2. This speed is independent of mass and charge.

Question 17.
Why is the path of a charged particle not a circle when its velocity is not perpendicular to the magnetic field?
Answer:

1. If a charged particle moves in a region of a uniform magnetic field such that its velocity is not perpendicular to the magnetic field, then the velocity of the particle is split up into two components.
2. One component is parallel to the field while the other component perpendicular to the field.
3. The component of velocity parallel to find remains unchanged and the component perpendicular to the field keeps changing due to Lorentz force.
4. Hence the path of the particle is not a circle; it is helical around the field lines.
   
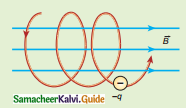
   Helical path of the electron in a uniform.

Question 18.
Give the properties of dia/para/ferromagnetic materials.
Answer:

Properties	Dia	Para	Ferro
Magnetic susceptibility	Negative	Positive and small	Positive and large
Relative permeability	Slightly less than unity	Greater than unity	Large
Nature of magnetic field lines	Repelled or expelled from diamagnetic materials	Attracted into the paramagnetic materials	Strongly attracted to the ferromagnetic materials
Susceptibility	Temperature independent.	Inversely proportional to temperature.	Inversely proportional to temperature.
Examples	Bismuth, copper, and water, etc.	Aluminum, platinum, chromium, etc.	Iron, Nickel, and Cobalt

Question 19.
What happens to the domains in a ferromagnetic material in the presence of an external magnetic field?
Answer:

1. The domains having magnetic moments parallel to the field glow bigger in size.
2. The other domains (not parallel to the field) are rotated so that they are aligned with the field.

Question 20.
How is a galvanometer converted into (i) an ammeter and (ii) a voltmeter?
Answer:

1. A galvanometer can be converted into an ammeter of a given range by connecting of suitable low resistance S called shunt in parallel to the galvanometer.
2. A galvanometer can be converted into suitable high resistance. R_h in series with the given galvanometer.

III. Long Answer Questions:

Question 1.
Discuss Earth’s magnetic field in detail.
Answer:

1. William Gilbert proposed that Earth behaves like a gigantic powerful bar magnet.
2. The temperature inside the earth is very high, so it is not possible for a magnet to retain its magnetism.
3. Gover suggested that the Earth’s magnetic field is due to hot rays coming out from the sun.
4. The branch of physics which deals with the Earth’s magnetic field is called Geomagnetism or Terrestrial magnetism.
5. Three quantities required to specify the Earth’s magnetic field are
   • magnetic declination (D)
   • magnetic dip or inclination (I)
   • the horizontal component of the Earth’s magnetic field (B_H)
6. B_E → Earth’smagneticfield.
   B_H → Horizontal component
   B_V → Vertical component
   Horizontal component B_H = B_E cos I
   Vertical component B_V= B_E sin I;
   \(\tan I=\frac{B_{V}}{B_{H}}\)
   i) At magnetic equator B_H = B_E [I = 0°]
   B_V = 0
   ii) At magnetic poles B_H = 0 [I = 90°]
   B_V = B_E

Question 2.
Deduce the relation for the magnetic field at a point due to an infinitely long straight conductor carrying current.
Answer:

1. Let NM be a long straight wire carrying a current I.
2. Let dl be the elemental length at a distance l from O.
3. Let P be a point at a distance ‘a’ from ‘o’.
4. According to Biot savart law, Magnetic Induction at P is
   \(\overrightarrow{\mathrm{dB}}=\frac{\mu_{\mathrm{o}} \mathrm{I\overrightarrow{\mathrm{dl}}}}{4 \pi \mathrm{r}^{2}} \sin \theta\) ………….(1)

The direction of the field is perpendicular to the plane of the paper and going into it.

From the figure, In △PAO,

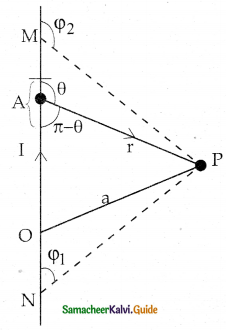
tan(π – θ) = \(\frac{a}{l}\)
∵ tan(π – θ) = -tan θ
-tan θ = \(\frac{a}{l}\)
l = \(\frac{-a}{\tan \theta}\)
l = -a cot θ ………………(2)

From △PAO
sin θ = \(\frac{a}{r}\)
\(r=\frac{a}{\sin \theta}\)
∴r = a cosec θ …………….(3)
Differentiating (2)
dl = a cosec²θ dθ …………..(4)

Question 3.
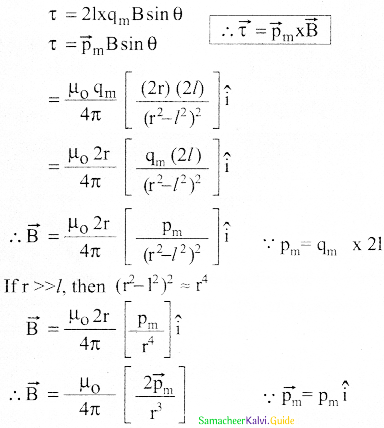
Obtain a relation for the magnetic field at a point along the axis of a circular coil carrying current.
Answer:

1. Let R be the radius of a current-carrying circular loop.
2. I be the current flowing through the wire.
3. Let P be a point on the axis of the circular coil at a distance z from its center ‘o’.
4. Take two diametrically opposite element d\(\overrightarrow{\mathrm{I}\) at C and D.
5. Let \(\overrightarrow{\mathrm{r}}\) be the vector joining the current I\(\mathrm{d} \overrightarrow{\mathrm{l}}\) at C.
   
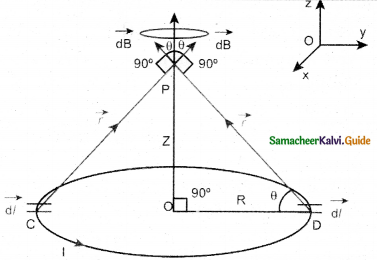
   Magnetic field due to current carrying circular loop using Biot-Savart’s law.
   
6. PC = PD = r = \(\sqrt{R^{2}+Z^{2}}\)
   ∠CPO =∠DPO = θ
7. According to Biot – Savart’s law,
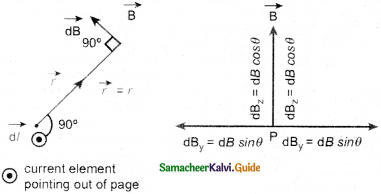
   \(\mathrm{d} \overrightarrow{\mathrm{B}}=\frac{\mu_{\mathrm{o}}}{4 \pi} \frac{\mathrm{Id} \overrightarrow{\mathrm{l}} \times \hat{\mathrm{r}}}{\mathrm{r}^{2}}\)
8. \(\mathrm{d} \overrightarrow{\mathrm{B}}\) is resolved into two components
   dB sin θ – along y – direction
   dB cos θ – along z – direction
9. Horizontal components cancel each other vertical component contribute to total magnetic field.
10. Integrating d\(\overrightarrow{\mathrm{I}\) around the ioop, d\(\overrightarrow{\mathrm{B}\) sweeps out a cone.
    
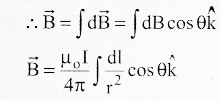
    (Using pythagorous)
    ∵\(\cos \theta=\frac{R}{\sqrt{R^{2}+Z^{2}}}\)
    r² = R² + Z²
    \(B=\frac{\mu_{0} I}{4 \pi} \int \frac{d l}{R^{2}+Z^{2}} \frac{R}{\sqrt{R^{2}+Z^{2}}} \hat{k}\)
    

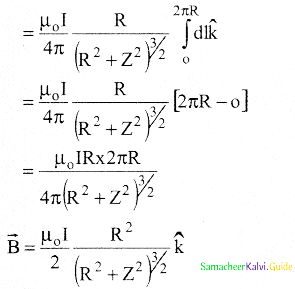
Question 4.
Compute the torque experienced by a magnetic needle in a uniform magnetic field.
Answer:

1. Consider a magnetic needle or bar magnet of length 2l.
2. Pole strength → q_m.
3. Each pole experience a force q_mB, but in opposite direction.
4. The net force is zero.
5. The magnetic needle will rotate and constitute a couple.
6. Force experienced by the north pole
7.  Force experienced by south pole

\(\overrightarrow{\mathrm{F}}_{\mathrm{N}}=\mathrm{q}_{\mathrm{m}} \overrightarrow{\mathrm{B}}\)
\(\begin{array}{l}
\overrightarrow{\mathrm{F}}_{\mathrm{S}}=-\mathrm{q}_{\mathrm{m}} \overrightarrow{\mathrm{B}} \\
\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{F}}_{\mathrm{N}}+\overrightarrow{\mathrm{F}}_{\mathrm{S}}
\end{array}\)
\(\overrightarrow{\mathrm{F}}\) = 0
\(\begin{aligned}
\text { Torque } \vec{\tau} &=\mathrm{O} \overrightarrow{\mathrm{N}} \times \overrightarrow{\mathrm{F}}_{\mathrm{N}}+\mathrm{O} \overrightarrow{\mathrm{S}} \times \overrightarrow{\mathrm{F}}_{\mathrm{S}} \\
&=\mathrm{O} \overrightarrow{\mathrm{N}} \mathrm{x} \mathrm{q}_{\mathrm{m}} \overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{OS}} \times\left(-\mathrm{q}_{\mathrm{m}} \overrightarrow{\mathrm{B}}\right)
\end{aligned}\)
Using right hand cork screw rule, total torque points into the paper.

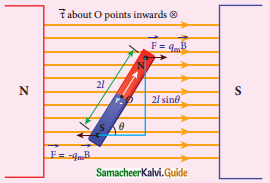
Magnetic dipole kept in a uniform magnetic field

\(\begin{array}{l}
|\mathrm{ON}|=|\mathrm{OS}|=l \\
\left|\mathrm{q}_{\mathrm{m}} \overrightarrow{\mathrm{B}}\right|=\mid-\mathrm{q}_{\mathrm{m}} \overrightarrow{\mathrm{B}}
\end{array}\)
∴\(\overrightarrow{\mathrm{τ}}\) = l × q_mBsin θ + l × q_mBsin θ

Question 5.
Calculate the magnetic field at a point on the axial line of a bar magnet.
Answer:

1. Consider a bar magnet NS.
2. N – Northpole, S – Southpole
3. Pole strength – q_m.
4. Distance – 2l
5. C be a point along the axis of the magnet.
6. By Coulomb’s law of magnetism,
7. The force of repulsion
   
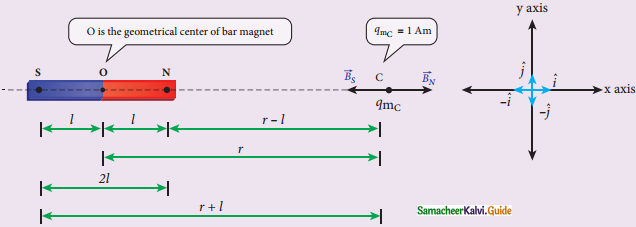
   Magnetic field at a point along the axial line due to magnetic dipole
   \(\overrightarrow{\mathrm{F}}_{\mathrm{N}}=\frac{\mu_{\mathrm{o}}}{4 \pi} \frac{\mathrm{q}_{\mathrm{m}}}{(\mathrm{r}-l)^{2}} \hat{\mathrm{i}}\) …………..(1)
8. r – l → is the distance between north pole of the bar magnet and unit north pole at C.
9. The force of attraction,
   \(\overrightarrow{\mathrm{F}}_{\mathrm{S}}=\frac{-\mu_{0}}{4 \pi} \frac{\mathrm{q}_{\mathrm{m}}}{(\mathrm{r}+l)^{2}} \hat{\mathrm{i}}\) ………………(2)
10. r + l → is the distance between south pole of the bar magnet and unit north pole at C.
11. Net force at point C.
    \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{F_N}}\) + \(\overrightarrow{\mathrm{F_S}}\)
    \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{B}}\)
    
    

Question 6.
Obtain the magnetic field at a point on the equatorial line of a bar magnet.
Answer:

1. Consider a bar magnet NS.
2. N – Northpole, S – Southpole
3. Pole strength – q.
4. Distance between two poles – 2l
5. C be a point along the equatorial line
6. By Coulomb’s law of magnetism,
7. The force of repulsion,

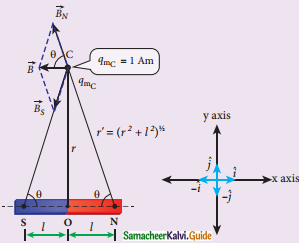
Magnetic field at a point along the equatorial line due to a magnetic dipole

\(\overrightarrow{\mathrm{F}}_{\mathrm{N}}=-\mathrm{F}_{\mathrm{N}} \cos \theta \hat{\mathrm{i}}+\mathrm{F}_{\mathrm{N}} \sin \hat{\theta} \hat{\mathrm{j}}\)
where,
\(\mathrm{F}_{\mathrm{N}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{q}_{\mathrm{m}}}{\mathrm{r’}^{2}}\) …………(1)

The force of attraction,
\(\overrightarrow{\mathrm{F}}_{\mathrm{S}}=-\mathrm{F}_{\mathrm{S}} \cos \theta \hat{\mathrm{i}}-\mathrm{F}_{\mathrm{S}} \sin \hat{\theta} \hat{\mathrm{j}}\)
where,
\(\mathrm{F}_{\mathrm{S}}=\frac{\mu_{\mathrm{o}}}{4 \pi} \frac{\mathrm{q}_{\mathrm{m}}}{\mathrm{r}^{\prime 2}}\) ……………(2)

The net force at point C,
\(\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{F}}_{\mathrm{N}}+\overrightarrow{\mathrm{F}}_{\mathrm{S}}\)
\(\overrightarrow{\mathrm{B}}\) = – (F_N + F_S) cosθî
Here,
\(\overrightarrow{\mathrm{F}}_{\mathrm{N}}=\overrightarrow{\mathrm{F}}_{\mathrm{S}}\)
∴ \(\begin{array}{l}
\overrightarrow{\mathrm{B}}=-\frac{2 \mu_{\mathrm{o}}}{4 \pi} \frac{\mathrm{q}_{\mathrm{m}}}{\mathrm{r}^{\prime 2}} \cos \theta \hat{\mathrm{i}} \\
\overrightarrow{\mathrm{B}}=-\frac{2 \mu_{\mathrm{o}}}{4 \pi} \frac{\mathrm{q}_{\mathrm{m}}}{\left(\mathrm{r}^{2}+1^{2}\right)} \cos \theta \hat{\mathrm{i}}
\end{array}\)

Question 7.
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
Answer:

1. I be the current flowing in a straight conductor of infinite length.
2. The wire is geometrically cylindrical in shape.
3. Symmetrical about an axis.
4. Amperian loop is constructed in the form of a circular shape at a distance r from the centre of
5. From Ampere’s law, \(\oint\) \(\overrightarrow{\mathrm{B}}\) . \(\overrightarrow{\mathrm{dl}}\) = μ₀I

Amerian loop for current-carrying straight line

\(\overrightarrow{\mathrm{dl}}\) is the line element along the loop.
The angle between magnetic field and line element is zero.
∴\(\oint\) B.dl = μ₀I
B is uniform over the loop
∴ B\(\oint\)dl = μ₀I
The circumference of the loop = 2πr
∴ \(\mathrm{B} \int_{0}^{2 \pi \mathrm{r}} \mathrm{dl}\) = μ₀I
B.2πr = μ₀I
\(\mathrm{B}=\frac{\mu_{\mathrm{o}} \mathrm{I}}{2 \pi \mathrm{r}}\)
In vector form,
\(\vec{B}=\frac{\mu_{0} I}{2 \pi r} \hat{n}\)
n̂ – unit vector along the tangent to the loop.

Question 8.
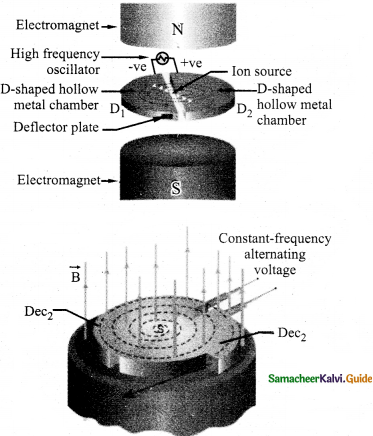
Discuss the working of a cyclotron in detail.
Answer:
Cyclotron:

1. A device used to accelerate the charged particles to gain large kinetic energy.
2. It is also called as high energy accelerator.

Principle:
When a charged particle moves normally to the magnetic field, it experiences magnetic Lorentz force.

Construction:

1. The particles are allowed to move in between two semi-circular metal containers called Dees.
2. Uniform magnetic field is controlled by an electromagnet.
3. The direction of magnetic field is normal to the plane of the Dees.
4. Source ‘S’ is kept between the two Dees.
5. Dees are connected to high frequency alternating potential difference.

Working:

1. The ion ejected from the source is positively charged.
2. It is accelerated towards a Dee-1 which has negative potential at that time.
3. The ion undergoes a circular path.
4. After one semi-circular path, the ion reaches the gap between the Dees.
5. The polarities of the Dees are reversed, so that ion accelerated towards Dee-2 with greater velocity.
6. The centripetal force is provided by Lorentz force 0 ; Bqv
   ∴ \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\mathrm{Bqv}\)
   \(r=\frac{m}{B q} v\)
   i.e. r α v
   
   
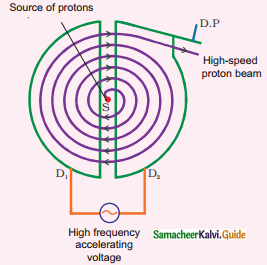
7. If the radius of the circular path increases, velocity also increases.
8. Particles undergo a spiral path with increasing radius.
9. Particles took out with the help of the deflector plate and hit the target T.

Limitations :

1. The speed of the ion is limited.
2. An electron cannot be accelerated.
3. Unchanged particles cannot be accelerated.

Question 9.
What is tangent law? Discuss in detail.
Answer:
Tangent law:-
When a magnetic needle or magnet is freely suspended in two mutually perpendicular uniform magnetic fields, it will come to rest in the direction of the resultant of the two fields.
B = B_H tan θ
Construction:

1. A circular coil of wire wound over brass or wood.
2. The circular turn table is adjusted through levelling screws.
3. Compass box at the center
4. Pivoted magnet and aluminium pointer are found.
5. The circular scale graduated with four quadrants.

Theory:

1. Two magnetic fields are perpendicular to each other.
2. Magnetic induction due to the current in the coil acting normal to the plane of the coil.
   
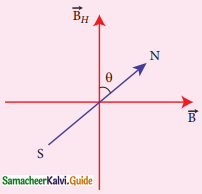
   B_H – horizontal component of Earth’s magnetic field.
   Magnetic induction at the centre of a coil
   B = \(\mathrm{B}=\mu_{\mathrm{o}} \frac{\mathrm{NI}}{2 \mathrm{R}}\) …………(2)
   ∴ Substituting (2) in (1)
   \(\begin{aligned}
   \mu_{0} \frac{\mathrm{NI}}{2 \mathrm{R}} &=\mathrm{B}_{\mathrm{H}} \tan \theta \\
   \mathrm{B}_{\mathrm{H}} &=\mu_{\mathrm{o}} \frac{\mathrm{NI}}{2 \mathrm{R}} \frac{1}{\tan \theta}
   \end{aligned}\) in tesla.

Question 10.
Derive the expression for the torque on a current-carrying coil in a magnetic field.
Answer:
Consider a rectangular loop PQRS carrying current I is placed in a uniform magnetic field B. Let a and b be the length and breadth rectangular loop respectively. The unit vector n̂ normal to the plane of the loop makes an angle θ with the magnetic field.

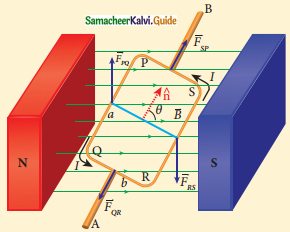
Rectangular coil placed in a magnetic field

1. The magnitude of the magnetic force acting on the current-carrying arm PQ is F_PQ = IaBsin (π/2) = IaB.
2. The magnitude of the force on the arm QR is F_QR =IbBsin \(\left(\frac{\pi}{2}-\theta\right)\) = IbB cos θ and its direction.
3. The magnitude of the force on the arm RS is F_RS =IaBsin( π/2) = IaB and its direction is downwards.
4. The magnitude of the force acting on the arm SP is F_SP = lbB\(\left(\frac{\pi}{2}-\theta\right)\) = IbB cos θ and its direction.
5. Since the forces F_QR and F_SP are equal, opposite, and collinear, they cancel each other. But the forces F_PQ and F_RS.

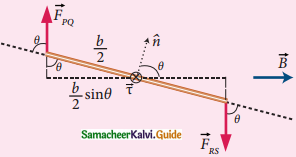
Side view of the current loop

6. The magnitude of torque acting on the arm PQ about AB is τ_PQ = (1/2 sinθ) and points in the direction of AB. The magnitude of the torque acting on the arm. RS about AB is τ_RS = (b/2 sinθ) IaB and points also in the same direction AB.
7. The total torque acting on the entire loop about an axis AB is given by
\(\tau=\left(\frac{b}{2} \sin \theta\right) F_{P Q}+\left(\frac{b}{2} \sin \theta\right) F_{R S}\)
= Ia(bsinθ)B
τ = IABsinθ along the direction B.
In vector form,
\(\overrightarrow{\mathrm{τ}}\) = (\(\overrightarrow{\mathrm{IA}}\)) × \(\overrightarrow{\mathrm{B}}\).
8. The above equation can also be written in terms of magnetic dipole moment.
\(\overrightarrow{\mathrm{τ}}\) = \(\overrightarrow{\mathrm{p_m}}\) × \(\overrightarrow{\mathrm{B}}\) where \(\overrightarrow{\mathrm{p_m}}\) = \(\overrightarrow{\mathrm{IA}}\)
9. If there are N turns in the rectangular loop, the torque is given by
τ = NIAB sinθ
Special cases:
a) When θ =90° or the plane of the loop is parallel to the magnetic field, the torque on the current loop is maximum.
τ_max = IAB
b) When θ = 0°/180° or the plane of the loop is perpendicular to the magnetic field, the torque on the current loop is zero.

Question 11.
Discuss the conversion of a galvanometer into an ammeter and also a voltmeter.
Answer:
Galvanometer to an ammeter:
1. The ammeter must offer low resistance, no change in current.
2. Galvanometer is converted to an ammeter by connecting low resistance in parallel.
3. Low resistance – Shunt resistance.
4. I – current in the circuit.
5. I_g – Galvanometer current.
6. R_g – Galvanometer resistance.
7. Current through the shunt, I_s = I – I_g
8. V_galvanometer = V_shunt
I_g R_g = (I – I_g)S
\(\mathrm{S}=\frac{\mathrm{I}_{\mathrm{g}} \mathrm{R}_{\mathrm{g}}}{\mathrm{I}-\mathrm{I}_{\mathrm{g}}}\) ………..(1)
\(\mathrm{I}_{\mathrm{g}}=\frac{\mathrm{S}}{\mathrm{S}+\mathrm{R}_{\mathrm{g}}} \mathrm{I}\)
I_g α I

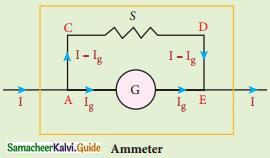
9. The deflection in the galvanometer is proportional to current θ α I_g
\(\begin{array}{l}
\frac{1}{\mathrm{R}_{\text {eff }}}=\frac{1}{\mathrm{R}_{\mathrm{g}}}+\frac{1}{\mathrm{~s}} \\
\frac{1}{\mathrm{R}_{\text {eff }}}=\frac{\mathrm{R}_{\mathrm{g}} \mathrm{S}}{\mathrm{R}_{\mathrm{g}}+\mathrm{S}}=\mathrm{R}_{\mathrm{a}}
\end{array}\)
10. R_a is very low.
11. An ideal ammeter has zero resistance.

Galvanometer to a voltmeter:

1. The voltmeter must have high resistance.
2. A galvanometer is converted to a voltmeter by connecting high resistance in series.
3. R_g – Galvanometer resistance.
4. I_g – Galvanometer current.
5. R_h – High resistance
6. Since it is connected in series, the current is the same.
   
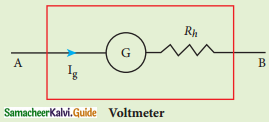
   i.e. I = I_g
   I_g = \(\frac{\text { Potential difference }}{\text { total resistance }}\)
   R_v = R_g + R_h
   \(\begin{array}{l}
   \mathrm{Ig}=\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{g}}+\mathrm{R}_{\mathrm{h}}} \\
   \mathrm{R}_{\mathrm{h}}=\frac{\mathrm{V}}{\mathrm{I}_{\mathrm{g}}}-\mathrm{R}_{\mathrm{g}}
   \end{array}\)
   ∴I_g α V
7. An ideal voltmeter has infinite resistance.

Question 12.
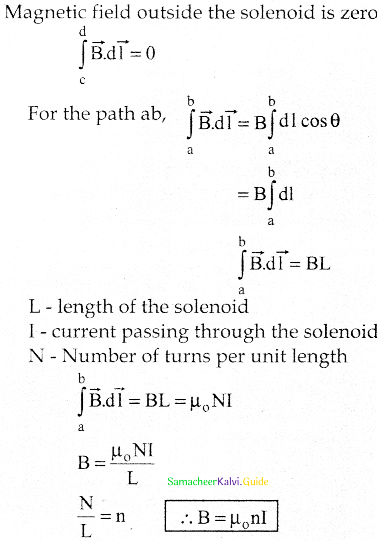
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law.
Answer:

1. Consider a solenoid of length L having N turns.
2. Solenoid’s diameter is much smaller compared to its length.
   The magnetic field inside the solenoid:
3. Consider a rectangular loop abcd.
4. From Ampere’s circuital law,
5. Elemental length bc and da are perpendicular to the magnetic field.
   ∴ \(\int_{b}^{c} \vec{B} \cdot d \vec{l}=\int_{b}^{c}|\vec{B}| d \vec{l} \mid \cos 90^{\circ}=0 \quad \int_{d}^{a} \vec{B} \cdot d \overrightarrow{1}=0\)
   
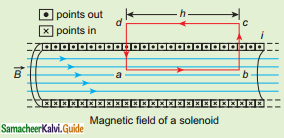
   Amperian loop for solenoid.
   \(\begin{array}{l}
   \oint \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{\mathrm{l}}=\mu_{\mathrm{O}} \mathrm{I}_{\text {enclosed }} \\
   \mathrm{C} \\
   \oint_{\mathrm{C}} \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{\mathrm{l}}=\int_{\mathrm{a}}^{b} \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{1}+\int_{\mathrm{b}}^{c} \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{\mathrm{l}}+\int_{\mathrm{c}}^{\mathrm{d}} \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{\mathrm{l}}+\int_{\mathrm{d}}^{\mathrm{a}} \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{1}
   \end{array}\)
   

Question 13.
Derive the expression for the force between two parallel, current-carrying conductors.
Answer:
1. Two long parallel current-carrying conductors separated by a distance V in air.
2. I₁, I₂ – current passing through the conductors A and B in the same direction.
3. Magnetic field due to current I2 of elemental length dl in A
\(\begin{array}{l}
\overrightarrow{\mathrm{B}}_{1}=\frac{\mu_{\mathrm{o}} \mathrm{I}_{1}}{2 \pi \mathrm{r}}(-\hat{\mathrm{i}}) \\
\overrightarrow{\mathrm{B}}_{1}=\frac{-\mu_{\mathrm{o}} \mathrm{I}_{1}}{2 \pi \mathrm{r}}(\hat{\mathrm{i}}
\end{array}\)
4. The direction of magnetic field is perpendicular to the plane of the paper and outwards.
5. A force on a small elemental length dl in B, experience magnetic field B₁.



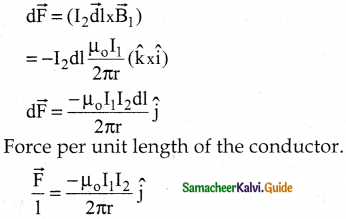
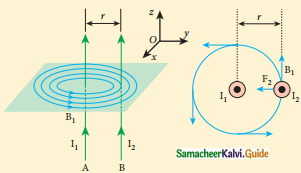
6. Attractive force – direction of electric current is same.
7. Repulsive force – direction of electric current is opposite.

Question 14.
Give an account of magnetic Lorentz force.
Answer:

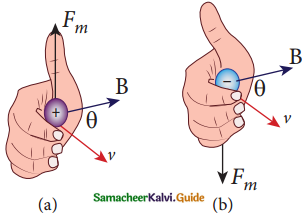
Direction of the Lorentz force on
(a) positive charge
(b) negative charge
1. An electric charge q is moving with velocity \(\overrightarrow{\mathrm{v}}\) in the magnetic field \(\overrightarrow{\mathrm{B}}\), experience a force called magnetic force \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) deduced by Lorentz.
\(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) = q (\(\overrightarrow{\mathrm{v}}\) × \(\overrightarrow{\mathrm{B}\)) …………(1)
\(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) = qvBsin θ ……………(2)
Equations (1) & (2) implies

2. \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) is directly proportional to the magnetic field \(\overrightarrow{\mathrm{B}}\).

3. \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) is directly proportional to the velocity \(\overrightarrow{\mathrm{V}}\).

4. \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) is directly proportional to sine of the angle between the velocity and magnetic field.

5. \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) is directly proportional to the magnitude of the charge q.

6. \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) is always perpendicular to \(\overrightarrow{\mathrm{V}}\) and \(\overrightarrow{\mathrm{B}}\).

7. The direction of \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) on negative charge is opposite to the direction of \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) on positive charge.

8. If velocity \(\overrightarrow{\mathrm{v}}\) of the charge is along magnetic field, \(\overrightarrow{\mathrm{F}}_{\mathrm{m}}\) = 0.

Question 15.
Compare the properties of soft and hard ferromagnetic materials.
Answer:

Properties	Soft ferromagnetic materials	Hard ferromagnetic materials
1. Absence of external field.	Magnetisation disappear	Magnetisation remains
2. Area of the loop	Small	Large
3. Retentivity	Low	High
4. Coercivity	Low	High
5. Susceptibility and magnetic permeability	High	Low
6. Hysteresis loss	Less	More
7. Uses	Solenoid core, transformer core, and electromagnets	Permanent magnet
8. Examples	Soft iron, Mumetal, Stelloy, etc.	Steel, Alnico, Lodestone, etc.

Question 16.
Derive an expression for the force acting on a current-carrying conductor placed in a magnetic field.
Answer:

1. The force experienced is equal to the sum of Lorentz forces on the individual charge carriers in the wire.
2. Consider a small length of wire ‘dl’, area – A, Current – I.
3. The free electrons drift opposite to the direction of the current.
4. The relation between I & V_d is given by
   I = neAV_d
   
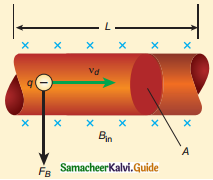
5. In magnetic field, the force experienced is given by
   \(\overrightarrow{\mathrm{F}}\) = -e(\(\overrightarrow{\mathrm{v}}_{\mathrm{d}}\) × \(\overrightarrow{\mathrm{B}}\))
   n → number of free electrons per unit volume.
   n = \(\frac{\mathrm{N}}{\mathrm{V}}\)
   V = A dl
6. Lorentz force = n A dl × – e(\(\overrightarrow{\mathrm{v}}_{\mathrm{d}}\) × \(\overrightarrow{\mathrm{B}}\))
   dF = -enA dl (\(\overrightarrow{\mathrm{v}}_{\mathrm{d}}\) × \(\overrightarrow{\mathrm{B}}\))
7. Current element, I\(\overrightarrow{\mathrm{dl}}\) = – enA\(\overrightarrow{\mathrm{v}}_{\mathrm{d}}\)
   ∴ d\(\overrightarrow{\mathrm{F}}\) = (I\(\overrightarrow{\mathrm{dl}}\) × \(\overrightarrow{\mathrm{B}}\))
   \(\overrightarrow{\mathrm{F}}\) = (I \(\overrightarrow{\mathrm{l}}\) × \(\overrightarrow{\mathrm{B}}\))
   F = BIl sin θ
   Case (i):
   If the conductor is along the magnetic field; θ = 0° ; F = 0.
   Case (ii):
   If the conductor is perpendicular to the magnetic field; θ = 90°; F = BIl.

IV. Numerical problems:

Question 1.
A bar magnet having a magnetic moment p_m is cut into four pieces i.e., first cut in two pieces along the axis of the magnet and each piece is further cut into two pieces. Compute the magnetic moment of each piece.
Answer:
If cut along the axis of the magnet of length ‘l’ into 4 pieces,
New pole strength M’= \(\frac{\mathrm{m}}{4}\)
New length l’ = l

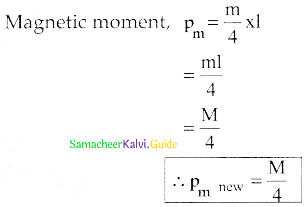
Question 2.
A conductor of linear mass density 0.2 g m1 suspended by two flexible wire as shown in figure. Suppose the tension in the supporting wires is zero when it is kept inside the magnetic field of I T whose direction is into the page. Compute the current inside the conductor and also the direction for the current.

Answer:
To have zero tension in the wires, the magnetic force per unit length must be upwards and equal to the weight per unit length.
∴\(\left|\frac{F_{\mathrm{m}}}{\mathrm{L}}\right|=\mathrm{BI}=\frac{\mathrm{mg}}{\mathrm{L}}\)
I = \(\frac{\left(\frac{\mathrm{m}}{\mathrm{L}}\right) \mathrm{g}}{\mathrm{B}}\)
\(\frac{\mathrm{m}}{\mathrm{L}}\) = 0.2 gm^-1
= 0.2 × 10^-3 kgm^-1
B = It
g = 10ms^-2
∴I = \(\frac{0.2 \times 10^{-3} \times 10}{1}\) = 2 × 10^-3 A
I = 2 mA

Question 3.
A circular coil with a cross-sectional area of 0.1 cm² is kept in a uniform magnetic field of strength 0.2 T. If the current passing in the coil is 3A and the plane of the loop is perpendicular to the direction of magnetic field. Calculate
a) total torque on the coil
b) total force on the coil
c) average force on each electron in the coil due to the magnetic field. The free electron density for the material of the wire is 10²⁸ m^-3.
Answer:
N= 1
A = 0.1 × 10^-4 m²
B = 0.2 T
I = 3A
θ = 0° [Plane is perpendicular to the field]
n = 10²⁸ m^-3
a) Torque, τ = NIB A sinθ
= l × 3 × 0.2 × 0. 1 × 10 × sin 0°
Torque = 0
b) Total force on a current loop is always zero in a magnetic field.
c) for free electron, drift velocity,
v_d = q(\(\overrightarrow{\mathrm{v}}\) × \(\overrightarrow{\mathrm{B}}\))
= qv_dB sin 90°
F = Bqv_d

= \(\frac{0.6}{0.1}\) × 10²⁸ × 10⁴
= 6 × 10^-24
Average Force, F = 0.6 × 10^-23 N.

Question 4.
A bar magnet is placed in a uniform magnetic field whose strength is 0.8 T. If the bar magnet is oriented at an angle 30° with the external field experiences a torque of 0.2 Nm. Calculate
i) the magnetic moment of the magnet
ii) the work is done by the magnetic field in moving it from the most stable configuration to the most its configuration and also compute the work done by the applied magnetic field in this case.
Answer:
i) τ = 0.2 Nm
τ = P_mB sinθ

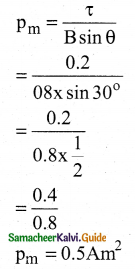
ii) W = U_f – U_i
U_f = μ_B cos 180°
U_i = -μ_B cos 0°
∴W = μ_B cos 180° – (μ_B cos 0°)
= μ_B + μ_B
W = 2μ_B;
W = 2 P_mB
W = 2 × 0.5 × 0.8
W = 0.85 J and
W_mag = -0.85 J

Question 5.
A non-conducting sphere has a mass of 100g and a radius of 20cm. A flat compact coil of wire with turns 5 is wrapped tightly around it with each turn concentric with the sphere. This sphere is placed on an inclined plane such that the plane of the coil is parallel to the inclined plane. A uniform magnetic field of 0.5 T exists in the region in a vertically upward direction. Compute the current I required to rest the sphere in equilibrium.
Answer:
The sphere is in translational equilibrium,
f_a – Mg sinθ = 0 ……………..(1)
The sphere is in rotational equilibrium.
torque = μB sinθ (Produces by magnetic field clockwise)
Frictional force (anticlockwise torque) = f_sR
R – radius of the sphere
f_sR – μB sinθ = 0 ……………..(2)
Substitute (1) in (2)
f_s = mg sinθ
∴ mg sinθ R – μB sinθ = 0
mg sinθ R = μB sinθ

μB = mgR ……………(3)
μ = NIA
μ = NIπr² …………….(4)
NIπr² = mgR
I = \(\frac{\mathrm{mgR}}{\mathrm{BN} \pi \mathrm{R}^{2}}\)
I = \(\frac{\mathrm{mg}}{\mathrm{BN} \pi \mathrm{R}}\)
m = 100g = 100 ×10^-3 kg
= 0.1 kg
R = 20 cm = 0.2m
B = 0.5 T
N = 5 turns
g = 10 m/s²

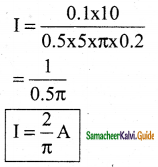
Question 6.
Calculate the magnetic field at the center of a square loop which carries a current of 1.5 A, length of each side being is 50cm.
Answer:

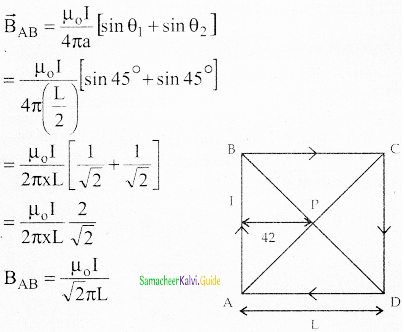
Similarly for four sides BC, CD, DA
B = \(\frac{4 \mu_{0} I}{\sqrt{2} \pi L}\)
Here,
I = 1.5A
L = 50 cm
L = 0.5 m
B = \(\frac{4 \mu_{0} I}{\sqrt{2} \pi L}\)
\(B=\frac{4 \times 4 \pi \times 10^{-7} \times 1.5}{\sqrt{2} \pi \times 0.5}\)
= \(\frac{24 \times 10^{-7}}{70.7 \times 10^{-2}}\)
= 0.3394 × 10^-7 × 10²
B = 3.39 × 10^-6 T
B = 3.4 × 10^-6 T

Part II:

12th Physics Guide Magnetism and Magnetic Effects of Electric Current Additional Questions and Answers

I. Choose the incorrect pair:

Question 1.
1. Aurora borealis – northern lights
2. Aurora australis – southern lights
3. Bluish-Orange – collision
4. Purplish – red – Nitrogen molecules
Answer:
Bluish orange – collision

Question 2.
1. Anticlockwise current – North pole
2. Clockwise current – South pole
3. Angular momentum – \(\frac{\mathrm{nh}}{2 \pi}\)
4. Bohr magneton – \(\frac{4 \pi \mathrm{m}}{\mathrm{eh}}\)
Answer:
Bohr magneton – \(\frac{4 \pi \mathrm{m}}{\mathrm{eh}}\)

Question 3.
1. Tangent law – B_H tan θ
2. Tangent galvanometer – Joule’s law
3. Magnetic polarity – End rule
4. Ampere’s – circuital law – Biot – Savart law
Answer:
Tangent galvanometer – Joule’s law

II. Choose the odd man out:

Question 1.
High permeability, high retentivity, low coercivity, thin hysteresis loop.
Answer:
High retentivity – property of permanent magnet. Others are properties of electromagnets.

Question 2.
William Gilbert, Gover, Hans Christian Oersted, George Simon ohm.
Answer:
George Simon Ohm – Electricity. Others explain the magnetic effect.

Question 3.
Aluminium, Platinum, Chromium, Bismuth
Answer:
Bismuth – Diamagnetic. Others are paramagnetic.

Question 4.
Phosphor bronze, suspension strip, torsion head, Dees
Answer:
Dees – Parts of the cyclotron. Others are parts of moving coil galvanometer.

III. Fill in the blanks:

Question 1.
When a charged particle enters in a uniform magnetic field, its kinetic energy ________________
Answer:
remain constant.

Question 2.
Work done by the magnetic Lorentz force is ________________
Answer:
zero.

Question 3.
The direction of the force on a current-carrying conductor placed in a magnetic field is given by ________________
Answer:
Fleming’s left-hand rule.

Question 4.
The tangent galvanometer is most sensitive at a deflection of ________________
Answer:
45°

IV. Match the following:

Question 1.

I	II
i. Magnetic dipole moment	a. NA-1 m-1
ii. Magnetic field	b. weber metre-2
iii. Magnetic flux	c. Am2
iv. Magnetic flux density	d. weber

Answer:
i. c
ii. a
iii. d
iv. b

Question 2.

I	II
i. Charge of an electron (e)	a. 9.27 x 10-24 Am2
ii. Gyromagnetic ratio (e/2m)	b. 9.11 x 10-31 kg
iii. Bohr magneton (μB)	c. 1.60 x 10-19 C
iv. Mass of an electron (m)	d. 8.78 x l010 Ckg-1

Answer:
i. c
ii. d
iii. a
iv. b

Question 3.

I	II
i. Diamagnetic	a. Aluminium
ii. Paramagnetic	b. Steel
iii. Soft Ferromagnetic	c. Copper
iv. Hard Ferromagnetic	d. Stelloy

Answer:
i. c
ii. a
iii. d
iv. b

Question 4.

I	II
i. Curie’s law	a. \(\frac{\mathrm{C}}{\mathrm{T}-\mathrm{T}_{r}}\)
ii. Coulomb law	b. \(\frac{\mathrm{Kq}_{\mathrm{m}_{\mathrm{A}}} \mathrm{q}_{\mathrm{m}_{\mathrm{B}}}}{r^{2}}\)
iii. Tangent law	c. C/T
iv. Curie – Weiss law	d. BH tan θ

Answer:
i. c
ii. b
iii. d
iv. a

V. Choose the correct pair:

Question 1.
1) Right-hand thumb rule – a. Direction of the magnetic moment
2) Gauss’s law – b. Electrostatics
3) Biot – Savart law – c. Direction of current
4) Maxwell’s right-hand cork screw rule – d. The direction of the magnetic field.
Answer:
Biot – Savart law – Direction of current

Question 2.
1. Radius (r) = \(\frac{\mathrm{qB}}{\mathrm{mV}}\)
2. Frequency (f_osc) = \(\frac{2 \pi \mathrm{m}}{\mathrm{qB}}\)
3. Time period (T) = \(\frac{\mathrm{qB}}{2 \pi \mathrm{m}}\)
4. Kinetic energy (K.E) = \(\frac{q^{2} B^{2} r^{2}}{2 m}\)
Answer:
Kinetic energy (K.E) = \(\frac{q^{2} B^{2} r^{2}}{2 m}\)

Question 3.
1. Figure of merit – deflection of two-scale division
2. Current sensitivity – Deflection produced per unit time
3. Voltage sensitivity – Deflection produced per unit voltage
4. Phosphor – bronze wire – Large couple per unit twist
Answer:
Voltage sensitivity – Deflection produced per unit voltage

Question 4.
1. Ammeter – measures the potential difference
2. Voltmeter – measure current
3. Shunt resistance – Parallel connection with a galvanometer
4. Ideal Ammeter – infinite resistance
Answer:
Shunt resistance – Parallel connection with galvanometer

Question 5.
1. Gyro – magnetic ratio – 8.78 × 10¹⁰ Ckg ^-1
2. Mass of an electron – 9.11 × 10³¹ kg
3 Planck’s constant – 6.63 × 10^-24 Js
4 Bohr magneton – 9.27 × 10^-34 Am²
Answer:
Gyromagnetic ratio – 8.78 × 10¹⁰ Ckg¹

VI. Assertion and Reason:

a) If both assertion and reason are true and the reason is the correct explanation of the assertion.
b) If both assertion and reason are true but the reason is not the correct explanation of the assertion.
c) If an assertion is true but the reason is false.
d) If the assertion and reason both are false.

Question 1.
Assertion:
Cyclotron does not accelerate electrons.
Reason:
The mass of the electron is very small.
Answer:
a) If both assertion and reason are true and the reason is the correct explanation of the assertion.

Question 2.
Assertion:
The poles of the magnet cannot be separated by breaking them into two pieces.
Reason:
The magnetic moment will be reduced to half when a magnet is broken into two equal pieces.
Answer:
b) If both assertion and reason are true but reason is not the correct explanation of the assertion.

Question 3.
Assertion:
When a magnet is brought near iron nails, only translatory force acts on it.
Reason:
The field due to a magnet is generally uniform.
Answer:
d) If the assertion and reason both are false.

Question 4.
Assertion:
The reduction factor of a tangent galvanometer helps in reducing deflection to current.
Reason:
Reduction factor increases with increase of current.
Answer:
c) If assertion is true but reason is false.

VII. Choose the correct statements:

Question 1.
(i) A freely suspended magnet always comes to rest in south-north direction.
(ii) Earth itself behaves like a gigantic powerful bar magnet.
(iii) Earth’s magnetic field is due to hot rays coming out from the sun.
(iv) The north pole of a magnetic compass needle is attracted towards the magnetic north pole of the earth.
Answer:
Statements (ii) and (iii) are correct.

Question 2.
(i) When \(\overrightarrow{\mathrm{B}}\) is parallel to the surface, θ = 90°, the magnetic flux, φ_B = 0.
(ii) Magnetic flux is a vector quantity.
(iii) The S.l Unit for magnetic flux is maxwell.
(iv) The CGS unit for magnetic flux is weber.
Answer:
Statement (i) is correct.

Question 3.
(i) T.G consists of a copper coil wounded on a magnetic circular frame.
(ii) T.G is provided with only one coil of a different number of turns.
(iii) A thin aluminium pointer is attached to the magnetic needle.
(iv) The frame is made up of silver.
Answer:
Statement (iii) is correct.

Question 4.
(i) For a fixed current I, the magnetic field outside the solenoid is constant.
(ii) The magnetic field of the solenoid demagnetizes the iron bar.
(iii) A solenoid is a long coil of wire closely wound in the form of a ring.
(iv) Solenoids can be used as electromagnets.
Answer:
Statement (iv) is correct.

VIII. Choose the incorrect statements:

Question 1.
i) Tangent galvanometer is a device for measuring current.
ii) The unit of reduction factor of T.G. is ampere.
iii) The tangent galvanometer is most sensitive at a deflection of 45°.
iv) The allowed deflection in T.G is between 45° and 55°.
Answer:
Statement (iv) is incorrect.

Question 2.
i) Permeability of a medium is μ₀ /μ_r
ii) Permeability of free space is 4π × 10^-7 henry / meter.
iii) Relative permeability of a medium is μ /μ₀
iv) The unit of magnetic induction is tesla.
Answer:
Statement (i) is incorrect.

Question 3.
i) The magnetic Lorentz force on a charged particle in the absence of an electric field is \(\overrightarrow{\mathrm{F}}\) = q(\(\overrightarrow{\mathrm{V}}\) × \(\overrightarrow{\mathrm{B}}\))
ii) The magnetic lorentz force on a charged particle in the presence of an electric field is F = q(\(\overrightarrow{\mathrm{V}}\) x \(\overrightarrow{\mathrm{B}}\)) + qE
iii) Work is done by the magnetic Lorentz force is infinite.
iv) The Lorentz force on a charged particle moving perpendicular to the magnetic field is maximum.
Answer:
Statement (iii) is incorrect.

Question 4.
i) In a circuit, the ammeter should be connected in series.
ii) Shunting means connecting a high resistance in parallel with the galvanometer.
iii) In a circuit, a voltmeter should be connected in parallel.
iv) The resistance of an ideal ammeter is zero.
Answer:
Statement (ii) is incorrect.

IX. Choose the best answer:

Question 1.
Magnetic induction at the center of the ring is shown in the diagram.

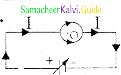
a) 0.2 T
b) 0.5 T
c) 0 T
d) 1.0 T
Answer:
c) 0 T

Question 2.
Magnetic field lines-
(a) cannot intersect at all
(b) intersect at infinity
(c) intersect within the magnet
(d) intersect at the neutral points
Answer:
(a) cannot intersect at all

Question 3.
When the number of turns in a galvanometer is doubled.
a) both current sensitivity and voltage sensitivity are doubled
b) current sensitivity does not change but voltage sensitivity is doubled
c) voltage sensitivity does not change but current sensitivity is doubled
d) both current sensitivity and voltage sensitivity do not change
Answer:
a) both current sensitivity and voltage sensitivity are doubled.

Question 4.
The magnetic declination angle for Chennai is
a) 1°8′
b) 2°8′
c) -1°8′
d) -2°8′
Answer:
c) -1°8′

Question 5.
Earth’s magnetic field always has a horizontal component except for at-
(a) equator
(b) magnetic pole
(c) a latitude of 60°
(d) a latitude of 50°
Answer:
(b) magnetic pole

Question 6.
The direction of magnetic moment is from ________to________
a) South pole, north pole
b) North pole, north pole
c) North pole, South pole
d) South pole, the south pole
Answer:
a) Southpole, north pole

Question 7.
A simple pendulum with charged bob is oscillating with time period T and lets O be the angular displacement. if the uniform magnetic field is switched on in a direction perpendicular to the plane of oscillation then
a) time period will decrease but θ will remain constant
b) time period will remain constant but θ will decrease
c) both time period and θ remain constant
d) both time period and θ will decrease
Answer:
c) both time period and θ remain constant

Question 8.
At magnetic poles the angle of dip is-
(a) 45°
(b) 30°
(c) 0°
(d) 90°
Answer:
(d) 90°

Question 9.
The magnitude and direction of Lorentz force is _______
a) \(\overrightarrow{\mathrm{F}}=q(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{V}})\)
b) \(F=q(\vec{B} \times \vec{V})\)
c) \(\overrightarrow{\mathrm{F}}=q(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{E}})\)
d) \(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{V}} \cdot \overrightarrow{\mathrm{B}})\)
Answer:
b) \(F=q(\vec{B} \times \vec{V})\)

Question 10.
1 Weber = _______.
a) 10⁶ maxwell
b) 10^-6 maxwell
c) 10⁸ maxwell
d) 10^-8 maxwell
Answer:
c) 10⁸ maxwell

Question 11.
Magnetic field at any point at a distance R due to a long straight conductor carrying current varies is
a) R²
b) R
c) \(\frac{1}{R^{2}}\)
d) \(\frac{1}{R}\)
Answer:
d) \(\frac{1}{R}\)

Question 12.
Demagnetization of a magnet can be done by-
(a) rough handling
(b) magnetizing in the opposite direction
(c) heating
(d) all the above
Answer:
(d) all the above

Question 13.
For free space, the relative permeability is ______
a) unity
b) zero
c) greater than one
d) constant
Answer:
a) unity

Question 14.
An arrangement of three parallel straight wires placed perpendicular to plane of paper carrying same current I along the same direction is shown in fig. Magnitude of force per unit length on the middle wire B is given by:

a) \(\frac{21^{2} \mu_{0}}{\pi d}\)
b) \(\frac{1^{2} \mu_{0}}{\sqrt{2 \pi d}}\)
c) \(\frac{\sqrt{21}^{2} \mu_{0}}{\pi \mathrm{d}}\)
d) \(\frac{1^{2} \mu_{0}}{2 \pi d}\)
Answer:
b) \(\frac{1^{2} \mu_{0}}{\sqrt{2 \pi d}}\)

Question 15.
The magnetic susceptibility of Aluminium is ______.
a) 2.3 × 10⁵
b) 2.3 × 10^-5
c) 2.2 × 10⁵
d) 2.2 × 10^-5
Answer:
b) 2.3 × 10^-5

Question 16.
Which of the following is most suitable for the core of an electromagnet?
(a) air
(b) soft iron
(c) steel
(d) Co-Ni alloy
Answer:
(b) soft iron

Question 17.
Dimension of Resistance is ______.
a) ML² T^-3 A^-2
b) ML² T^-1 A^-1
c) ML² T² A^-3
d) ML² T^-1 A^-2
Answer:
a) ML² T^-3 A^-2

Question 18.
Photo has spin _______.
a) S = \(\frac{1}{2}\)
b) S = –\(\frac{1}{2}\)
c) S = 1
d) S = 2
Answer:
c) S = 1

Question 19.
At Curie point, a ferromagnetic material becomes-
(a) non magnetic
(b) diamagnetic
(c) paramagnetic
(d) antiferromagnetic
Answer:
(c) paramagnetic

Question 20.
The variation of magnetic susceptibility (k) with magnetizing field (H) for a paramagnetic substance is _______

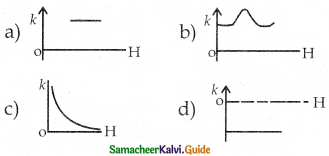
Answer:

Question 21.
The force per unit length between two conductors carrying one ampere current each and separated by a distance of 1 m is
a) 2π × 10^-7 N
b) 2 × 10^-7 N
c) 4π × 10⁷ N
d) 2π × 10⁷ N
Answer:
b) 2π × 10^-7 N

Question 22.
A cyclotron cannot accelerate _______.
a) electrons
b) protons
c) deuterons
d) α – particles
Answer:
a) electrons

Question 23.
\(\oint \overrightarrow{\mathbf{B}} \cdot \overrightarrow{\mathbf{d}}l\) is equal to
a) μI₀
b) μ₀I₀
c) \(\frac{\mu_{\mathrm{o}}}{\mathrm{I}_{\mathrm{o}}}\)
d) \(\frac{\mathrm{I}_{\mathrm{o}}}{\mu_{\mathrm{o}}}\)
Answer:
b) μ₀I₀

Question 24.
A magnetic needle is placed in a uniform magnetic field. It experience-
(a) a force and a torque
(b) a force but not a torque
(c) a torque but not a force
(d) neither a force nor a torque
Answer:
(c) a torque but not a force

Question 25.
In a galvanometer, the magnetic field used is _____
a) radial
b) parallel
c) perpendicular
d) tangential
Answer:
a) radial

Question 26.
In a tangent galvanometer, a current 1A produces a deflection of 30° the current required to produce a deflection of 60° is
a) 3 A
b) 2 A
c) √2A
d) √3A
Answer:
a) 3A

Question 27.
A magnetic needle suspended freely-
(a) orients itself in a definite direction
(b) remains in any direction
(c) become vertical with N-pole up
(d) become vertical with N-pole down
Answer:
(a) orients itself in a definite direction

Question 28.
The voltmeter resistance is
a) R_g = R_v +R_h
b) R_v = R_g+ R_h
c) R_h = R_v + R_g
d)R_g = R_h – R_v
Answer:
b) R_v = R_g+ R_h

Question 29.
Kirchoff’s I an II laws are based on conservation of
a) charge and energy
b) energy and charge
c) energy and voltage
d) energy and current
Answer:
a) charge and energy

Question 30.
A moving charge produces-
(a) an electric field only
(b)a magnetic field only
(c) both electric and magnetic fields
(d) neither an electric nor a magnetic field
Answer:
(c) both electric and magnetic fields

X. Two Mark Questions:

Question 1.
Define magnetic declination (D).
Answer:
The angle between magnetic meridian at a point and geographical meridian is called the declination or magnetic declination (D).

Question 2.
What is a magnetizing field?
Answer:

1. The magnetic field is used to magnetize a sample or specimen.
2. Vector quantity and denoted by \(\overrightarrow{\mathrm{H}}\).
3. Unit – Am^-1

Question 3.
What is relative permeability?
Answer:

1. The ratio between absolute permeability of the medium to the permeability of free space.
2. \(\mu_{\mathrm{r}}=\frac{\mu}{\mu_{\mathrm{o}}}\)
3. For free space, μ_r = 1
4. Isotropic medium, μ → scalar.
5. Non-isotropic medium, μ → tensor.

Question 4.
What is the intensity of magnetisation?
Answer:

1. The net magnetic moment per unit volume of material.
2. \(\overrightarrow{\mathrm{M}}=\frac{\text { magnetic moment }}{\text { volume }}=\frac{1}{\mathrm{~V}} \overrightarrow{\mathrm{p}}_{\mathrm{m}}\)
3. Unit – Am^-1

Question 5.
State Curie’s law.
Answer:

1. The magnetic susceptibility decreases with increase in temperature.
2. \(\begin{array}{l}
   \mathrm{X}_{\mathrm{m}} \alpha \frac{1}{\mathrm{~T}} \\
   \mathrm{X}_{\mathrm{m}}=\frac{\mathrm{C}}{\mathrm{T}}
   \end{array}\)
3. C – curie constant, T – Kelvin.

Question 6.
Define in terms of magnetising field.
Answer:
The magnetic field which is used to magnetize a sample or specimen is called the magnetising field. Magnetising field is a vector quantity and it denoted by \(\vec { H } \) and its unit is A m^-1.

Question 7.
What kind of magnetic properties electromagnet has?
Answer:
Materials should possess

• High initial permeability
• Thin hysteresis loop.
• Low retentivity
• Low coercivity
• Examples: Soft iron and Mumetal (Nickel Iron alloy)

Question 8.
What is needed to design transformer cores?
Answer:

1. Large magnetic induction
2. High initial permeability
3. Thin hysteresis loop with a small area.

Question 9.
State ‘One ampere’.
Answer:
One ampere is defined as that current when it is passed through each of the two infinitely long parallel straight conductors kept at a distance of one meter apart in a vacuum causes each conductor to experience a force of 2 x 10^-7 newton per meter length of the conductor.

Question 10.
Define magnetic dipole moment of the current loop.
Answer:
The product of the current and area of the loop.

Question 11.
What is a solenoid?
Answer:
A long coil of wire closely wound in the form of a helix.

Question 12.
What is toroid?
Answer:
Both the ends of a solenoid are joined together to form a closed ring shape.

Question 13.
Define one tesla.
Answer:
Unit charge moving with unit velocity experiences unit force.
\(1 \mathrm{~T}=\frac{1 \mathrm{Ns}}{\mathrm{Cm}}=1 \frac{\mathrm{N}}{\mathrm{Am}}=1 \mathrm{NA}^{-1} \mathrm{~m}^{-1}\)

Question 14.
State Lorentz force.
Answer:

1. The total force experienced by the charge.
2. \(\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{q}} \mathrm{E}(\overrightarrow{\mathrm{V}} \times \overrightarrow{\mathrm{B}})\)

Question 15.
Give the expression for cyclotron frequency or gyro frequency.
Answer:
f = \(\frac{\mathrm{qB}}{2 \pi \mathrm{m}}\)
ω = 2πf = \(\frac{\mathrm{qB}}{\mathrm{m}}\)

Question 16.
Give the uses of the mass spectrometer.
Answer:
A mass spectrometer is used in many areas

1. In sciences; especially in medicine, space science, geology, etc.
2. In medicine, anaesthesiologists use it to measure respiratory gases.
3. Biologists use it to determine the reaction mechanisms in photosynthesis.

Question 17.
How is a galvanometer is converted into an ammeter and a voltmeter?
Answer:

1. A galvanometer is converted into an ammeter by connecting a low resistance in parallel with the galvanometer.
2. A galvanometer is converted into a voltmeter by connecting a high resistance Rh in series with the galvanometer.

Question 18.
What is the reason for the hemispherical magnetic poles used in moving coil galvanometer?
Answer:

1. The hemispherical magnetic poles produce a radial magnetic field.
2. The plane of the coil is parallel to the magnetic field in all its positions.

Question 19.
Why did we use the coils in different thicknesses in the Tangent galvanometer?
Answer:
The coil consists of 2, 5, and 50 turns of different thicknesses to measure the current of different strengths.

Question 20.
The electrons cannot be accelerated by a cyclotron, why?
Answer:

1. At high frequencies, a relativistic variation of the mass of the electron is appreciable.
2. Hence electrons cannot be accelerated by a cyclotron.

Question 21.
Why Phosphor bronze wire is used as suspension wire in moving coil galvanometer?
Answer:

1. Because phosphor bronze wire produces a small couple per unit twist.
2. A small couple per unit twist increases the sensitivity of the galvanometer.

Question 22.
Why freely suspended bar magnets in your lab experience only torque but not any translatory motion even though Earth has a non-uniform magnetic field?
Answer:
Earth’s magnetic field in the lab is uniform. Therefore, it experiences torque and not a translatory motion.

Question 23.
List the differences between coulomb force and Lorentz force.
Answer:

Coulomb force	Lorentz force
1. Force between two charged particles separated by a distance.	Force experienced by current carrying conductor placed in a uniform magnetic field.
2. It decreases with an increase in distance.	It remains constant.
3. It depends upon the medium.	It doesn’t depend upon the medium.

Question 24.
What is the Meissner effect?
Answer:
The expulsion of magnetic flux from a superconductor during its transition to the superconducting state.

Question 25.
Difference between Tangent Galvanometer and Moving coil galvanometer.
Answer:

Tangent Galvanometer	Moving coil galvanometer
1. It works on the principle of Tangent law.	It works on the principle that when a current carrying coil suspended in a uniform magnetic field
2. It consists of a non-magnetic circular frame.	It consists of a rectangular coil of fine insulated copper wire.
3. It is used to measure magnetic induction.	It is used to measure potential.

Question 26.
Difference between the natural magnet and artificial magnet.
Answer:

Natural magnet	Artificial magnet
1. Formed in nature.	Man-made magnets.
2. It has no regular size and shape.	It has the perfect size and shape.
3. Ex: Magnetite or lode stone	Ex: Bar magnet.

XI. Three Mark Questions:

Question 1.
State Curie-Weiss law.
Answer:

1. The susceptibility of the material above the curie temperature is given by
2. \(X_{m}=\frac{C}{T-T_{C}}\)
   This relation is called the Curie – Weiss law.
3. C – Curie constant
   T – Temperature
   Tc – Curie temperature

Question 2.
Define in terms of the Current Sensitivity of a galvanometer.
Answer:
It is defined as the deflection produced per unit current flowing through it.
I_s = \(\frac { θ }{ I }\) = \(\frac { N A B }{ K }\) ⇒ I_s = \(\frac { 1 }{ G }\)

Question 3.
What are the applications of hysteresis loop?
Answer:

1. It provides information such as retentivity, coercivity, permeability, susceptibility, and energy loss.
2. It helps to select and suitable material for a given purpose.

Question 4.
State Maxwell’s right-hand corkscrew rule.
Answer:

1. If a right-handed corkscrew is rotated, the direction of current is the same as the direction in which the screw advances and the direction of rotation of the screw gives the direction of the magnetic field.
2. This rule is used to determine the direction of the magnetic field.

Question 5.
Write short notes on MRI (Magnetic Resonance Imaging).
Answer:

1. It helps to diagnose or monitor treatment for a variety of abnormal conditions in the head, chest, abdomen, and pelvis.
2. It consists of a superconducting wire to produces a strong magnetic field.
3. It uses radiofrequency pulses and a computer to produce pictures of organs.

Question 6.
Difference between Coulomb’s law and Biot-Savart’s law.
Answer:

Coulomb’s law	Biot -Savart’s law
1. It is produced by a scalar source, ie. an electric charge q.	It is produced by a vector source ie) current element I \(\overrightarrow{\mathrm{dl}}\).
2. It is directed along the position vector joining the source and the point at which the field is calculated.	It is directed perpendicular to the position vector \(\overrightarrow{\mathrm{r}}\) and the current element I \(\overrightarrow{\mathrm{dl}}\).
3. It does not depend on the angle.	It depends on the angle between the position vector \(\overrightarrow{\mathrm{r}}\) and the current element I \(\overrightarrow{\mathrm{dl}}\).

Question 7.
List out the deflection based on the velocity – velocity selector.
Answer:

Velocity	Deflection of charged particle
1. V >V0	In the direction of Lorentz force.
2. V < V0	In the direction of Coulomb force.
3. V = V0	No deflection and the particle moves straight.

Question 8.
Define the current sensitivity of a galvanometer.
Answer:

1. The deflection produced when unit current passes through the galvanometer.
2. The galvanometer produces a large deflection for a small current.
3. Current sensitivity.
   \(\frac{\theta}{\mathrm{I}}=\frac{\mathrm{NBA}}{\mathrm{K}}\)

Question 9.
How can the current sensitivity of the galvanometer increase?
Answer:

1. By increasing the number of turns.
2. By increasing the magnetic induction.
3. By increasing the area of the coil.
4. By decreasing the couple per unit twist of the suspension wire.

Question 10.
Define voltage sensitivity of a galvanometer?
Answer:

1. The deflection per unit voltage.
2. Voltage sensitivity
   \(\frac{\theta}{\mathrm{V}}=\frac{\theta}{\mathrm{IR}_{\mathrm{g}}}=\frac{\mathrm{NBA}}{\mathrm{KR}_{\mathrm{g}}}\)
3. Rg – Galvanometer resistance.

Question 11.
Why does the voltage sensitivity remain constant even if the number of turns in increased?
Answer:

1. When the number of turns is doubled, current sensitivity also doubled.
2. If the number of turns (n) increases, the resistance (G) increases.
   Hence voltage sensitivity remains constants.
3. Voltage sensitivity = \(\frac{\mathrm{NBA}}{\mathrm{KR}_{\mathrm{g}}}\)

Question 12.
In a galvanometer, the current sensitivity does not necessarily increase the voltage sensitivity. Give reason.
Answer:

1. Current sensitivity does not depend on Resistance. It depends on the number of turns.
2. Voltage sensitivity decreases with an increase in resistance. But this is made constant by increasing the number of turns.
3. There is no increase in voltage sensitivity.

Question 13.
Derive an expression for a magnetic dipole in a current loop.
Answer:

1. Consider a circular loop of radius R.
2. The magnetic field along the axis is given by
   
   

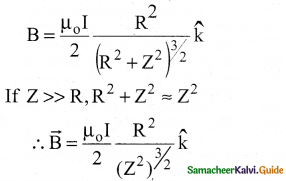
Question 14.
Why magnetic field outside the solenoid is zero?
Answer:

1. The magnetic field lines exist outside the solenoid.
2. But the number of field lines per unit area outside the solenoid is much less compared to the number of field lines per unit area inside the solenoid.
3. Therefore the magnetic field is very much small, so it is considered to be zero.

Question 15.
Why the resistance of the voltmeter be very large?
Answer:

1. The resistance of the voltmeter should be very large compared to the resistance of the voltmeter which is connected across to measure the potential difference.
2. The current through the circuit decreases and the voltmeter shows a low potential difference.
3. The error is eliminated, when the voltmeter has a high resistance.
4. An ideal voltmeter has infinite resistance.

Question 16.
Two wires of equal length are bent in the form of two loops. One loop is square whereas the other is circular. These are suspended in the same magnetic field and the same current is passed through them. Explain with the reason which will experience greater torque?
Answer:
For a given length, the circle has the greatest area.
τ = NIAB.
Torque is directly proportional to area. So, the circular current loop experiences greater torque.

Question 17.
What are the precautions to be taken while handling the Tangent galvanometer?
Answer:

1. Keep away all the nearly magnets and magnetic materials.
2. Using a spirit level, by adjusting the levelling screw, the small magnetic needle is exactly horizontal and the coil is exactly vertical.
3. Make the coil remain in the magnetic meridian.
4. By rotating the coil, the plane of the coil is parallel to the small magnetic needle.
5. The compass is rotated such that the pointer reads O° – O°.

Question 18.
Define figure of merit of a galvanometer? Which has more resistance, a galvanometer or a millimeter?
Answer:

1. The current produces a deflection of one scale division in the galvanometer.
2. The millimeter can detect a very small amount of current.
3. Its resistance is low compared to a galvanometer.
4. ∴ A galvanometer has more resistance than a millimeter.

Question 19.
Mention the factors on which the direction of force experienced by a current-carrying conductor placed in a magnetic field.
Answer:
The direction of force experienced by the current-carrying conductor depends on

• direction of current
• the direction of the magnetic field.

Question 20.
A coil of insulated copper wire is connected to a galvanometer. What will happen if a bar magnet is pushed into the coil?
Answer:

1. The magnetic field lines linked with the coil change.
2. Electric current to get induced in it.
3. The needle of the galvanometer will move momentarily in one direction.

XII. Five Mark Questions:

Question 1.
What are the properties of a magnet?
Answer:

1. A freely suspended bar magnet will always point along the north-south direction.
2. The attractive force is maximum near the end of the bar magnet.
3. A magnet attracts another magnet or magnetic substance towards itself.
4. When a magnet is broken into pieces, each piece behaves like a magnet with poles at its ends.
5. Two poles of a magnet have pole strength equal to one another.
6. The length of the bar magnet is called a geometrical length.
7. The length between two magnetic poles in a bar magnet is called magnetic length.
8. The ratio of magnetic length and geometrical length is \(\frac{5}{6}=0.833\)

Question 2.
List out the properties of magnetic field lines.
Answer:

1. Continuous closed curves.
2. The direction is from the North to South pole – outside the magnet.
3. The direction is from the south to north pole – inside the magnet.
4. The direction of the magnetic field at any point is known by the tangent to the magnetic line of force at that point.
5. Magnetic field lines never intersect.
6. The magnetic field is strong where the magnetic field lies crowd.
7. The magnetic field is weak where magnetic field lines thin out.

Question 3.
Obtain an expression for the potential energy of a bar magnet in a uniform magnetic field.
Answer:

1. A bar magnet has a dipole moment \(\overrightarrow{\mathrm{P_m}}\)
2. It makes an angle θ with the uniform magnetic field B.
3. The torque acting on the dipole
   
   

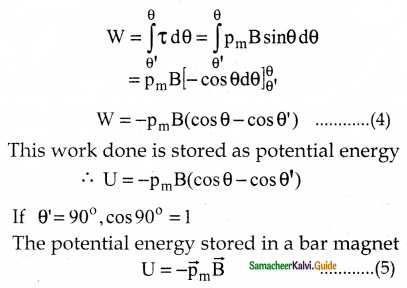
case i:
If θ = 0°
U = -P_mB cos0 = -P_mB ………….(6)
Potential energy is minimum when aligned along the external magnetic field.
case ii:
If θ=180°
U = -P_mB(c0s 180°) = -P_mB(-1)
U = P_m
Potential energy is maximum when aligned antiparallel to the external magnetic field.

Question 4.
Discuss the variation of magnetic induction \(\overrightarrow{\mathrm{B}}\) with magnetising field H in a ferromagnetic material, with the graph.
Answer:

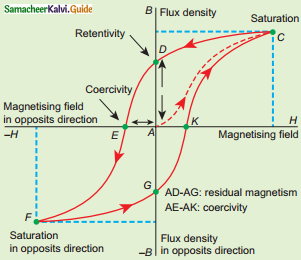
1. A ferromagnetic material is magnetised slowly.
2. The magnetic induction \(\overrightarrow{\mathrm{B}}\) increases from point A, then attains a saturated level.
3. This is plotted as AC in the graph.

Saturation magnetization:

1. The maximum point up to which the material can be magnetised.
2. Further on reducing magnetising field, the magnetic induction also decreases.
3. It does not retrace the original path CA. It takes a different path CD.
4. When the magnetising field is zero, the magnetic induction is not zero. It has a positive value.

Remanence or Retentivity:

1. The ability of the materials to retain the magnetism when \(\overrightarrow{\mathrm{H}}\) = 0 . (AD)
2. To demagnetise the material, \(\overrightarrow{\mathrm{H}}\) gradually increases in reverse direction.
3. \(\overrightarrow{\mathrm{B}}\) decreases along DE and at E, \(\overrightarrow{\mathrm{B}}\) = 0.
4. AE brings the residual magnetism to zero.

Coercivity:

1. For the reverse magnetising field, the residual magnetism vanishes.
2. On increasing \(\overrightarrow{\mathrm{H}}\), \(\overrightarrow{\mathrm{B}}\) also increases along EF, till the saturation point at F.
3. If \(\overrightarrow{\mathrm{H}}\) decreased or increased, it traces the path FGKC.
4. This closed curve ACDEFGK is called hysteresis loop, (cycle of magnetisation)
5. In this cycle, \(\overrightarrow{\mathrm{B}}\) lags behind \(\overrightarrow{\mathrm{B}}\)
6. Lagging of \(\overrightarrow{\mathrm{B}}\) behind \(\overrightarrow{\mathrm{B}}\) is called hysteresis.
7. Hysteresis means “lagging behind”.

Question 5.
Discuss the magnetic field around
i) a straight conductor carrying current
ii) circular coil carrying current.
Answer:
i) Current carrying straight conductor:

1. When a magnetic compass is kept near a current-carrying conductor, it experiences a torque.
2. It aligns in the direction of the magnetic field.
3. The nature of the magnetic field is like concentric circles having their center at the axis of the conductor.
   
   
4. The direction of a magnetic field is clockwise or anticlockwise depending on the direction of the current.
5. If current increases, the magnetic field is also increased.
6. If distance increases, the magnetic field decreases.

ii) Circular coil carrying:

1. When a magnetic compass is kept near a current-carrying conductor, it experiences a torque.
2. It aligns in the direction of the magnetic field.
3. The magnetic field lines are circular at points A and B.
4. The magnetic field lines are nearly parallel to each other near the center.
5. If the current or number of turns increases, the magnetic field increases.
6. The polarity depends on the direction of the current in the loop.

Question 6.
Deduce the magnetic dipole moment of a revolving electron.
Answer:
1. Electron revolves around a nucleus in a circular orbit of radius R.
2. Circulating electron is like a current in a circular loop.
3. The magnetic dipole moment
μ_L = IA …………….(1)
4. If T is the time period if an electron, then-current
\(I=\frac{-\mathrm{e}}{\mathrm{T}}\) ……………..(2)
-e → Charge of an electron


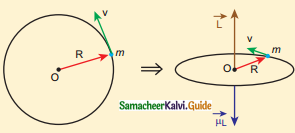
5. Angular momentum, L = Rp; L = mvR

\(\mu_{\mathrm{L}}=\frac{\text { neh }}{4 \pi \mathrm{m}}\)

6. On substituting known values,
μ_L = n × 9.27 × 10_-24 Am²
7. When n=1, μ_L = n × 9.27 × 10_-24 Am² (or)
μ_L = 9.27 × 10_-24 JT^-1
8. (μ_L)_min = μ_B (Bohr magneton)
μ_B = \(\frac{\mathrm{eh}}{4 \pi \mathrm{m}}\) = 9.27 × 10_-24 Am²

Question 7.
Deduce the magnetic field inside, interior, and exterior region in the toroid.
Answer:
i) Open space interior to the toroid:

1. Consider Amperian loop 1 with radius r₁
2. To find the magnetic field B_p at P, the length of the loop is given by
   L₁ = 2πr_{1(circumference)} By Ampere’s circuital law,
   \(\begin{aligned}
   &\oint \overrightarrow{\mathrm{B}}_{\mathrm{P}} \cdot \overrightarrow{\mathrm{d}} l=\mu_{\mathrm{o}} \mathrm{I}_{\text {enclosed }}\\
   &\text { loop1 }
   \end{aligned}\)
3. Loop 1 encloses no current, so I_enclosed = 0.
   \(\oint \overrightarrow{\mathrm{B}} \mathrm{p} \cdot \overrightarrow{\mathrm{d}} l=0\)
4. This is possible only if, \(\overrightarrow{\mathrm{B}} p\) = 0
   

ii) Open space exterior to the toroid:

1. Construct on Amperian loop 3 of radius r₃ around the point Q.
2. To find the magnetic field B_Q at Q₁ the length of the loop is given by,
   L₃ = 2πr₃
   By Ampere’s circuital law,
   \(\left.\oint_{\text {loop } 3} \overrightarrow{\mathrm{B}}_{\mathrm{Q}} \cdot \overrightarrow{\mathrm{d}}\right]=\mu_{0} \mathrm{I}_{\text {enclosed }}\)
3. Current coming out and going into the plane of paper, I_enclosed = 0
   \(\oint_{\text {loop3 }} \overrightarrow{\mathrm{B}}_{\mathrm{Q}} \overrightarrow{\mathrm{d}} l=0\)
4. This is possible only if, B_Q = 0

iii) Inside the toroid:

1. Construct an Amperian loop 2 of radius r₂ around the point S.
2. To find the magnetic field B_s at S, the length of the loop is given by
3. By Ampere’s circuital law,
   \(\left.\oint_{\text {loop } 2} \overrightarrow{\mathrm{B}}_{\mathrm{S}} \cdot \overrightarrow{\mathrm{d}}\right]=\mu_{0} \mathrm{I}_{\text {enclosed }}\)
4. Let I – current passing through the toroid,
   N – Number of turns of the toroid.
   I_enclosed = NI
   
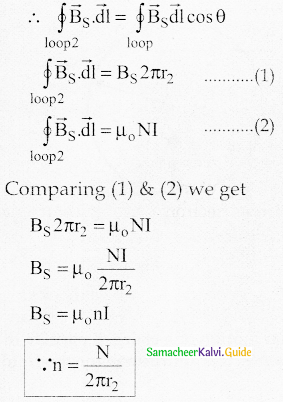
5. n → number of turns per unit length.

Question 8.
Discuss the motion of a charged particle in a uniform magnetic field.
Answer:

1. Consider a charged particle ‘q’ having mass’m’ enters into uniform magnetic field \(\overrightarrow{\mathrm{B}}\) with velocity \(\overrightarrow{\mathrm{v}}\).
2. Velocity is perpendicular to both magnetic field \(\overrightarrow{\mathrm{B}}\) and velocity \(\overrightarrow{\mathrm{v}}\).
3. The charged particle moves in a circular orbit.
4. The Lorentz force on the charged particle
   \(\overrightarrow{\mathrm{B}}\) = q(\(\overrightarrow{\mathrm{v}}\) × \(\overrightarrow{\mathrm{B}}\)) …………(1)
5. The magnitude of the net force is
   F_m = qvB …………….(2)
6. This Lorentz force exhibits as centripetal force to execute circular motion.
   qvB = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) …………….(3)
7. The radius of circular path
   \(r=\frac{m v}{B q}\) ……………(4)
   ∴ \(r=\frac{p}{B q}\) ……………..(5)
   
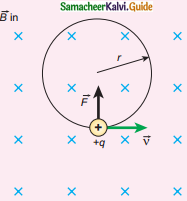
   Circular motion of a charged particle in a perpendicular uniform magnetic field.
8. p = mv is the linear momentum of the particle.
9. Let T be the time taken to complete one circular motion.
   
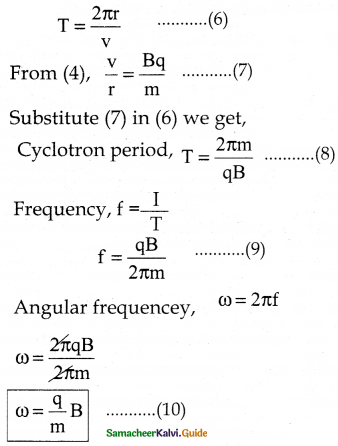
10. Eqns., (9) & (10) are called as cyclotron frequency or gyro frequency.
11. Time period and frequency depend only on charge-to-mass ratio and independent of Velocity or radius.

Question 9.
Discuss the motion of a charged particle under a crossed electric and magnetic field.
Answer:

1. Consider a charged particle ‘q having mass’m’ enters into uniform magnetic field \(\overrightarrow{\mathrm{B}}\) with velocity \(\overrightarrow{\mathrm{v}}\).
2. Velocity is not perpendicular to both magnetic field \(\overrightarrow{\mathrm{B}}\) and velocity \(\overrightarrow{\mathrm{v}}\).
3. The path of the particle is a helix.
4. The Lorentz force is balanced by the Coulomb force by electric and magnetic fields.
5. The Coulomb force acts along the direction of a magnetic field.
6. The Lorentz force is perpendicular to the direction of magnetic field.
7. To balance these forces, both electric and magnetic fields are perpendicular to each other.
8. Perpendicular electric and magnetic fields are known as cross fields.
9. In a parallel plate capacitor, the magnetic field is perpendicular to the electric field.
10. The net force \(\overrightarrow{\mathrm{F}}\) = q(\(\overrightarrow{\mathrm{E}}\) + \(\overrightarrow{\mathrm{v}}\) × \(\overrightarrow{\mathrm{B}}\))
11. For a positive charge, an electric force acts downward, the Lorentz force acts upward.
                                           
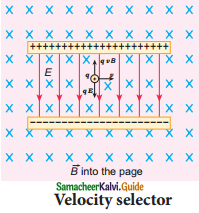
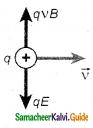
12. Two fields balance each other qE = – qv₀B
    \(\mathrm{v}_{\mathrm{o}}=\frac{\mathrm{E}}{\mathrm{B}}\)
    Force can experience only for the particle moving with v₀
13. There are three possibilities of deflection for the charged particle.
    • v > v₀ – Direction of Lorentz force
    • v < v₀ – Direction of Coulomb force
    • v = v₀ – No deflection, moves straight.

XIII. Additional Problems (one mark):

Question 1.
A current of 10A is flowing in a wire of length 1.5 M. A force of 15 N acts on it when it is placed in a uniform magnetic field of 2 teslas. The angle between the magnetic field and the direction of current is
a) 30°
b) 45°
c) 60°
d) 90°
Answer:
a) 30°
Solution:
F = BIL sin θ
sin θ = \(\frac{\mathrm{F}}{\mathrm{BIl}}\)
= \(\frac{15}{2 \times 10 \times 1.5}\)
sin θ = 1/2
θ = 30°

Question 2.
3 A of current is flowing in a linear conductor having a length of 40 cm. The conductor has placed in a magnetic field of
strength 500 gauss and makes an angle of 30° with the direction of the field. It experiences a force of magnitude _____.
a) 3 × 10⁴ newton
b) 3 × 10² newton
c) 3 × 10^-2 newton
d) 3 × 10^-4 newton
Answer:
c) 3 × 10^-2 newton
Solution :
F = Bil sin θ
= 500 × 10^-4 × 3 × (40 × 10^-2) × sin 30°
= 500 × 10^-4 × 3 × 40 × 10^-2 × \(\frac{1}{2}\)
F = 3 × 10^-2 N

Question 3.
A circular coil of a radius of 4 cm has 50 turns. In this coil, a current of 2A is flowing. It is placed in a magnetic field of 0.1 weber/m². The amount of work done in rotating it through 180° from its equilibrium position will be ______.
a) 0.1 J
b) 0.2 J
c) 0.4 J
d)0.3 J
Answer:
a) 0.1 J
Solution:
M = NIA
= NI(πr²)
W = MB(1 – cosθ)
= MB(1 – cos(180°))
= MB(1 – (-1))
= MB(2)
W = 2MB
W = 2(NIπr²)B
= 2 × (50 × 2 × 3.14 × 16 × 10^-4) × 0.1
W =0.1 J.

Question 4.
Two straight parallel wires, both carrying current lOA in the same direction attract each other with a force of 1 x 103 N. If both currents are doubled, the force of attraction will be
a) 1 × 10^-3N
b) 2 × 10^-3N
c) 4 × 10^-3N
d) 0.25 × 10^-3N
Answer:
c) 4 × 10^-3N
Solution:

Question 5.
A wire of length I meter carrying a current of I ampere is bent in the form of a circle. Its magnitude of the magnetic moment will be ______.
a) \(\frac{\mathrm{IL}}{4 \pi}\)
b) \(\frac{\mathrm{IL}^{2}}{4 \pi}\)
c) \(\frac{\mathrm{I}^{2} \mathrm{~L}^{2}}{4 \pi}\)
d) \(\frac{\mathrm{I}^{2} \mathrm{~L}}{4 \pi}\)
Answer:
b) \(\frac{\mathrm{IL}^{2}}{4 \pi}\)
Solution:
If the radius of the circle is r, then
2πr = L
r = \(\frac{\mathrm{L}}{2 \pi}\)
A = πr²
= \(\frac{\pi \mathrm{L}^{2}}{4 \pi^{2}}\)
A = \(\frac{\mathrm{L}^{2}}{4 \pi}\)
Magnetic moment M = IA
M = \(\frac{\mathrm{IL}^{2}}{4 \pi}\)

Question 6.
Two materials X and Y are magnetised whose intensity of magnetization is 500Am^-1 and 2000 Am^-1 respectively. The magnetising field is 1000 Am^-1. What is the ratio between the susceptibilities of the two materials?
Answer:
The susceptibility of material χ is
∴ Areas,
\(\begin{array}{l}
\chi_{m, x}=\frac{|\overrightarrow{\mathrm{M}}|}{|\overrightarrow{\mathrm{H}}|}=\frac{500}{1000}=0.5 \\
\chi_{\mathrm{m}, \mathrm{y}}=\frac{|\overrightarrow{\mathrm{M}}|}{|\overrightarrow{\mathrm{H}}|}=\frac{2000}{1000}=2
\end{array}\)
Since, the susceptibility of material Y is greater than that of material X, which implies that material Y Can be easily magnetized. The ratio between the susceptibilities of the two materials = 0.5 : 2.

Question 7.
An electron has a mass of 9 x 10^-31 kg and charges 1.6 x 10^-19 C is moving with a velocity of 10⁶ m/s. enters a region where a magnetic field exists. if it describes a circle of radius 0.10 m, the intensity of the magnetic field must be______
a) 1.8 × 10^-4 T
b) 5.6 × 10^-5 T
c) 14.4 × 10^-5 T
d) 1.3 × 10^-6 T
Answer:
b) 5.6 × 10^-5 T
Solution:
B = \(\frac{\mathrm{mv}}{\mathrm{qr}}\)
= \(\frac{9 \times 10^{-31} \times 10^{6}}{1.6 \times 10^{-19} \times 0.1}\)
B = 5.6 × 10^-5 tesla

Question 8.
A galvanometer coil of resistance 12Ω gives full-scale deflection for 3 mA. How will you convert it into a voltmeter of range 0 to 18 V and an ammeter of range 0 to 6A?
Answer:
Given:
G = 12Ω
I_g = 3 × 10^-3 A
V = 18V
I = 6A
i) R = \(\frac{\mathrm{V}}{\mathrm{I}_{\mathrm{g}}}\) – Galvanometer
= \(\frac{18}{3 \times 10^{-3}}\) – 12
= 6 × 10^-3 – 12
= 6000 – 12
R = 5988Ω
A resistance of 5988Ω should be connected in series with the galvanometer.

ii)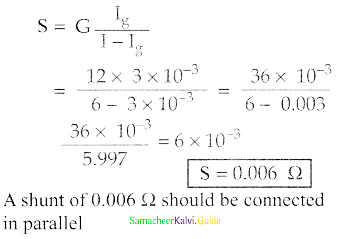

Question 9.
An alpha particle travels in a circular path of radius 0.45 m in a magnetic field B=1.2 wb/m² with a speed of 2.6 x 10⁷ m/s. The period of revolution of an alpha particle is _____.
(µ₀ = 4π × 10^-7weber / ampere-metre)
a) 4π × 10^-5 tesla
b) 8π × 10^-5 tesla
c) 4 × 10^-5 tesla
d) 2 × 10^-5 tesla
Answer:
a) 4π × 10^-5 tesla
Solution:
B = \(\frac{\mu_{\mathrm{o}} \mathrm{NI}}{2 \mathrm{r}}\)
= \(\frac{4 \pi \times 10^{-7} \times 100 \times 0.1}{2 \times 5 \times 10^{-2}}\)
B = 4π × 10^-5 tesla

Question 10.
The strength of the magnetic field at a point r near a long straight current-carrying wire is B. The field at a distance \(\frac{r}{2}\) will be _____.
a) \(\frac{\mathrm{B}}{2}\)
b) \(\frac{\mathrm{B}}{4}\)
c) 2B
d) 4B
Answer:
c) 2B
Solution:

XIV. Additional Problems (5 marks):

Question 1.
A circular coil carrying current has a radius R. Find the distance from the center of the coil on the axis, where the magnetic induction will be \(\frac{1}{8}\)th to its value at the center of the coil?
Answer:
\(\frac{B_{\text {centre }}}{B_{\text {axis }}}=\left(1+\frac{x^{2}}{R^{2}}\right)^{3 / 2}\)

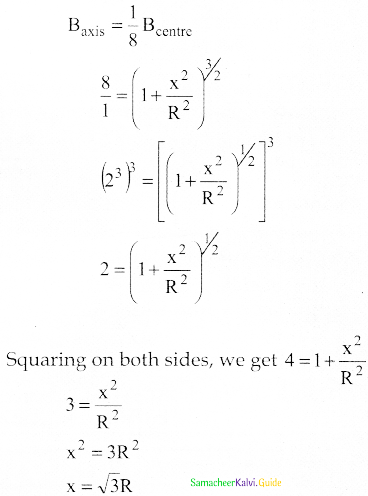
Question 2.
A coil having N turns is wound tight in the form of a spiral with inner and outer radii a and b respectively when a current I passes through the coil, Find the magnetic field at the center.
Answer:
Number of turns per unit width = \(\frac{\mathrm{N}}{\mathrm{b}-\mathrm{a}}\)
Consider an elemental ring of radius x, thickness dx.
Number of turns in the ring dN = \(\frac{\mathrm{Ndx}}{\mathrm{b}-\mathrm{a}}\)
The magnetic field at the center due to the ring element.

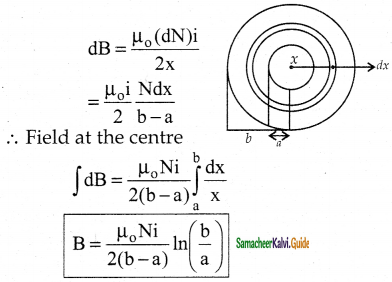
Question 3.
An electron moving perpendicular to a uniform magnetic field 0.5 T undergoes circular motion of radius 2.5 mm. What is the speed of the electron?
Answer:
Charge of an electron q = 1.6 × 10^-19 C
Magnitude of magnetic field, B = 0.5 T
Mass of an electron, m = 9.11 × 10^-31 Kg
Radius of the orbit, r = 2.5 mm =2.50 × 10^-3 m
Velocity of the electron, v = \(\frac{\mathrm{qrB}}{\mathrm{m}}\)
v = \(\frac{1.6 \times 10^{-19} \times 2.50 \times 10^{-3} \times 0.5}{9.11 \times 10^{-31}}\)
v = 2.195 × 10⁸ ms^-1

Question 4.
A circular coil of radius 20 cm has 100 turns wire and it carries a current of 5 A. Find the magnetic induction at a point along its axis at a distance of 20 cm from the center of the coil.
Answer:

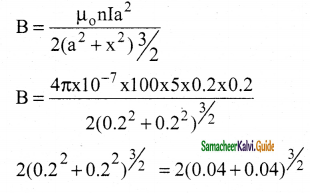
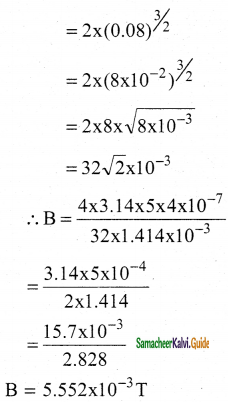
Question 5.
Three tangent galvanometers have turned 2 : 3 : 5. When connected in series in a circuit, they show deflections of 30°, 45°, and 60° respectively. Find the ratio of their radii.
Answer:

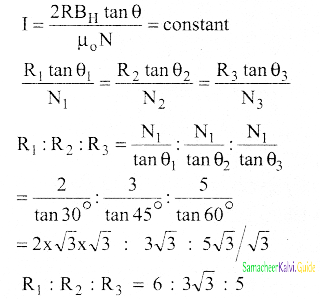
Question 6.
Show that the magnetic field at any point on the axis of the solenoid having n turns per unit length is
\(\mathbf{B}=\frac{1}{2} \mu_{0} \mathrm{nI}\left(\cos \theta_{1}-\cos \theta_{2}\right)\)
A solenoid is a long cylindrical coil having number of circular turns.
Answer:
n → number of turns per unit length
R → radius of a solenoid.
The current carrying element dx at a distance x from origin and distance r from point P.
\(r=\sqrt{R^{2}+\left(x_{0}-x\right)^{2}}\)
The magnetic field due to current carrying circular coil is
\(\mathrm{dB}=\frac{\mu_{\mathrm{o}} \mathrm{IR}^{2}}{2 \mathrm{r}^{3}} \mathrm{xN}\)
N = ndx
\(\mathrm{dB}=\frac{\mu_{0}}{2} \frac{\mathrm{nIR}^{2}}{\mathrm{r}^{3}} \mathrm{dx}\)
sin θ = \(\frac{R}{r}\)
r = R cosecθ

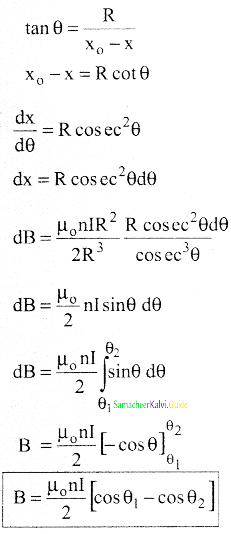
Question 7.
Let I₁ and I₂ be the steady currents passing through a long horizontal wire XY and PQ, respectively. Suppose the wire PQ is fixed in a horizontal plane and the wire XY is allowed to move freely in a vertical plane. Let the wire XY is in equilibrium at a height d over the parallel wire PQ as shown in the figure.

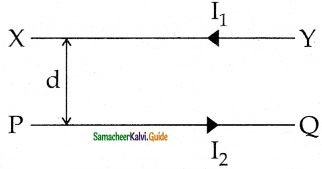
Show that if the wire XY is slightly displaced and released, it executes Simple Harmonic Motion (SHM). Also, compute the time period of oscillations.
Answer:
If XY is allowed to move freely in a vertical plane.
∴Vertical oscillation of the wire xy experience a force,
F = – ky
Applying Newton’s second law