Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Physics Guide Pdf Chapter 4 Electromagnetic Induction and Alternating Current Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 4 Electromagnetic Induction and Alternating Current
12th Physics Guide Electromagnetic Induction and Alternating Current Text Book Back Questions and Answers
Part – I
Text Book Evaluation:
I. Multiple choice questions:
Question 1.
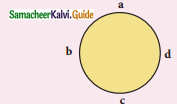
An electron moves on a straight line path XY as shown in the figure. The coil abcd is adjacent to the path of the electron. What will be the direction of current, if any, induced in the coil?
![]()
a) The current will reverse its direction as the electron goes past the coil
b) No current will be induced
c) abcd
d) adcb
Answer:
a) The current will reverse its direction as the electron goes past the coil
Solution:
First current develops in direction of abcd but when electron moves away, magnetic field inside loop decreases and current changes its direction.
Question 2.
A thin semi-circular conducting ring (PQR) of radius r is falling with its plane vertical in a horizontal magnetic field B, as shown in the figure. The potential difference developed across the ring when its speed v, is
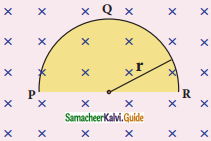
a) Zero
b) \(\frac{\mathrm{B} v \pi \mathrm{r}^{2}}{2}\) and P is at higher potential
c) πrBυ and k is at higher potential
d) 2rBυ and R is at higher potential
Answer:
d) 2rBυ and R is at higher potential
Solution:
Motional emt induced in the semi circular ring PQR is equal to the motional emt induced in the imaginary conductor PR.
EPQR = EPR = BVl = BV (2r) (l = PR = 2r)
∴ Potential difference developed across the ring is 2r Br with R is at higher potential.
Question 3.
The flux linked with a coil at any instant t is given by φB= 10t2 – 50t + 250. The induced emf at t = 3s is
a) -190 V
b) -10 V
c) 10 V
d) 190 V
Answer:
b) -10V
Solution:
e = – \(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = \(\frac{d}{d t}\) (10t2 – 50t + 250)
e = -20t + 50
e = -10V
Question 4.
When the current changes from +2A to -2A in 0.05 s, an emf of 8 V is induced in a coil. The coefficient of self-induction of the coil is
a) 0.2 H
b) 0.4 H
c) 0.8 H
d) 0.1 H
Answer:
d) 0.1 H
Solution:
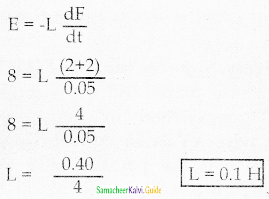
Question 5.
The current i flowing in a coil varies with time as shown in the figure. The variation of induced emf with time would be
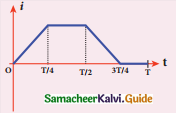
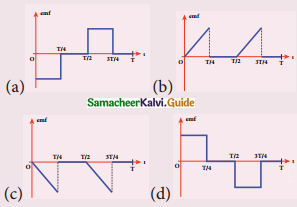
Answer:
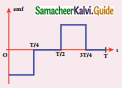
Solution:
For \(\frac{3 \mathrm{~T}}{4}\) to T i = 0, \(\frac{d i}{d t}\) = 0, e = 0
Question 6.
A circular coil with a cross-sectional area of 4 cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross-sectional area of 10 cm2. The axis of the coil coincides with the axis of the solenoid. What is their mutual inductance?
a) 7.54 μH
b) 8.54 μH
c) 9.54 μH
d) 10.54 μH
Answer:
a) 7.54 μH
Solution:
M = μ0 N1 N2 A2
=4π × 10-7 × 15 × 102 × 10 × 4 × 10-4
= 4π × 6 × 10-7
= 24 × 3.14 × 10-7
= 75.36 × 10-7
= 7.54 × 10-6
M = 7.54 μH
![]()
Question 7.
In a transformer the number of turns in the primary and the secondary are 410 and 123C respectively. If the current in primary is 6A, then that in the secondary coil is
a) 2A
b) 18A
c) 12A
d) 1A
Answer:
a) 2 A
Solution:
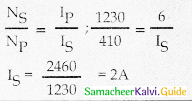
Question 8.
A step – down transformer reduces the supply voltage from 220 V to 11 V and increase the current from 6 A to loo A. Then its efficiency is
a) 1.2
b) 0.83
c) 0.12
d) 0.9
Answer:
b) 0.83
Solution:
P = VI
Input Power = 220 × 6 = 1320
Output Power = 11 × 100 = 1100
η = \(\frac{1100}{1320}\) = 0.83
Question 9.
In an electrical circuit, R, L, C, and AC voltage sources are all connected in series. When L is removed from the circuit, the phase difference between the voltage and current in the circuit is π/3. Instead, if C is removed from the circuit, the phase difference is again π/3. The power factor of the circuit is
a) 1/2
b) \(\frac{1}{\sqrt{2}}\)
c) 1
d) \(\frac{\sqrt{3}}{2}\)
Answer:
c) 1
Solution:
It is the condition for resonance therefore phase difference between v and i = 0
Power factor cos Φ = 1
Question 10.
In a series RL circuit, the resistance and inductive reactance are the same. Then the phase difference between the voltage and current in the circuit is
a) \(\frac{\pi}{4}\)
b) \(\frac{\pi}{2}\)
c) \(\frac{\pi}{6}\)
d) zero
Answer:
a) \(\frac{\pi}{4}\)
Solution:
tan Φ = \(=\frac{X_{L}}{R}\)
χL = R tan Φ = 1, Φ = 45°
Φ = \(\frac{\pi}{4}\)
Question 11.
In a series resonant RLC circuit, the voltage across 100Ω resistor is 40 V. The resonant frequency is 250 rad/s. If the value of C is 4μF, then the voltage across L is
a) 600 V
b) 4000 V
c) 400 V
d) 1 V
Answer:
c) 400 V
Solution:
χc = \(\frac{1}{C \omega}\) = 1000Ω
At resonant χc = χL
∴ I = \(\frac{V}{R}\) = 0.4 A
∴ VL = IXL = 400 V
Question 12.
An inductor 20 mH, a capacitor 50 µF, and a resistor 40Ω are connected in series across a source of emf V = 10 sin 340 t. The power loss in the AC circuit is
a) 0.76 W
b) 0.89 W
c) 0.46 W
d) 0.67 W
Answer:
c) 0.46 W
Solution:
Power loss = \(\left(\frac{E_{\mathrm{rms}}}{Z}\right) \mathrm{R}\)
Erms = \(\frac{10}{\sqrt{2}}\)
Z = \(\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
χL = 6.82Ω
χC = 58.8Ω
∴ Z = 65.6Ω
∴ Power Loss = 0.46 W
![]()
Question 13.
The instantaneous values of alternating current and voltage in a circuit are
i = \(\frac{1}{\sqrt{2}}\) sin(100πt) A and
v = \(\frac{1}{\sqrt{2}}\) sin(100π + π/3) V
The average power in watts consumed in the circuit is
a) \(\frac{1}{4}\)
b) \(\frac{\sqrt{3}}{4}\)
c) \(\frac{1}{2}\)
d) \(\frac{1}{8}\)
Answer:
d) \(\frac{1}{8}\)
Solution:
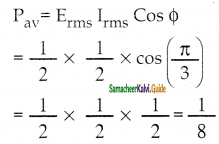
Question 14.
In an oscillating IC circuit, the maximum charge on the capacitor is Q. The charge on, the capacitor when the energy is stored equally between the electric and magnetic fields is
a) \(\frac{Q}{2}\)
b) \(\frac{Q}{\sqrt{3}}\)
c) \(\frac{Q}{\sqrt{2}}\)
d) Q
Answer:
c) \(\frac{Q}{\sqrt{2}}\)
Solution:
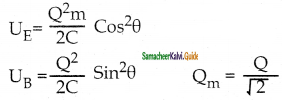
Question 15.
\(\frac{20}{\pi^{2}}\) H inductor is connected to a capacitor of capacitance C. The value of C in order to
impart maximum power at 50 Hz is
a) 50 µF
b) 0.5 µF
c) 500 µF
d) 5 µF
Answer:
d) 5 µF
Solution:
Maximum power at χL = χC
L 2πγ = \(\frac{1}{2 \pi \gamma}\)
C = 5 µF
![]()
II. Short Answer Questions:
Question 1.
What is meant by electromagnetic induction?
Answer:
Whenever the magnetic flux linked with a closed coil changes, an emf (electromotive force) is induced and hence an electric current flows in the circuit.
Question 2.
State Faraday’s laws of electromagnetic induction.
Answer:
First law:
Whenever magnetic flux linked with a closed circuit changes, an emf is induced in circuit.
Second law:
The magnitude of induced emf in a closed circuit is equal to the time rate of change of magnetic flux linked with the circuit
\(E=-\frac{\mathrm{d} \theta}{\mathrm{dt}}\)
Question 3.
State Lenz’s law.
Answer:
Lenz’s law states that the direction of the induced current is such that it always opposes the cause responsible for its production.
Question 4.
State Fleming’s right-hand rule.
Answer:
- The Thumb, index finger, and middle finger of the right hand are stretched perpendicular to each other.
- The index finger indicates the direction of the magnetic field.
- Thumb indicates the direction of motion of the conductor.
- The middle finger indicates the direction of induced current.
Question 5.
How is Eddy’s current produced? How do they flow in a conductor?
Answer:
Even for a conductor in the form of a sheet or plate, an emf is induced when magnetic flux linked with it changes. But the difference is that there is no definite loop or path for induced current to flow away. As a result, the induced currents flow in concentric circular paths. As these electric currents resemble eddies of water, these are known as Eddy currents. They are also called Foucault currents.
![]()
Question 6.
Mention the ways of producing induced emf.
Answer:
- By changing the magnetic field B.
- By changing the area A of the coil and
- By changing the relative orientation of the coil.
Question 7.
What for an inductor is used? Give some examples.
Answer:
Inductor is a device used to store energy in a magnetic field when an electric current flows through it. The typical examples are coils, solenoids, and toroids.
Question 8.
What do you mean by self-induction?
Answer:
- Its magnetic flux is changed by changing the current in the coil, and induced emf is induced in the same coil.
- This is known as self-induction.
Question 9.
What is meant by mutual induction?
Answer:
When an electric current passing through a coil changes with time, an emf is induced in the neighbouring coil. This phenomenon is known as mutual induction.
Question 10.
Give the principle of AC generator.
Answer:
- AC generator works on the principle of electromagnetic induction.
- The relative motion between a conductor and a magnetic field changes the magnetic flux linked with the conductor which in turn, induces an emf.
![]()
Question 11.
List out the advantages of stationary armature -rotating field system of AC generator.
Answer:
- The current is drawn directly from fixed terminals on the stator without the use of brush contacts.
- The insulation of stationary armature winding is easier.
- The number of sliding contacts (slip rings) is reduced. Moreover, the sliding contacts are used for low-voltage DC Source.
- Armature windings can be constructed more rigidly to prevent deformation due to any mechanical stress.
Question 12.
What are step-up and step-down transformers?
Answer:
- A transformer that increases the voltage by decreasing current is known as a step-up transformer.
- A transformer that decreases the voltage by increasing the current is a step-down transformer.
Question 13.
Define the average value of an alternating current.
Answer:
The average value of alternating current is defined as the average of all values of current over a positive half-cycle or negative half-cycle.
Question 14.
How will you define the RMS value of an alternating current?
Answer:
The RMS value of an alternating current is defined as the square root of the mean of the squares of all currents over one cycle.
I rms = \(\frac{\mathrm{I}_{\mathrm{m}}}{\sqrt{2}}\)
Question 15.
What are phasors?
Answer:
A sinusoidal alternating voltage (or current) can be represented by a vector which rotates about the origin in an anti-clockwise direction at a constant angular velocity ω. Such a rotating vector is called a phasor.
![]()
Question 16.
Define electric resonance.
Ans:
When frequency of applied alternating source (ωr) is equal to natural frequency
\(\left(\frac{1}{\sqrt{L C}}\right)\)
of RLC circuit, the current in the circuit reaches its maximum value. Then the circuit is said to be in electrical resonance.
Question 17.
What do you mean by resonant frequency?
Answer:
When the frequency of the applied alternating source (ωr) is equal to the natural frequency \(\left[\frac{1}{\sqrt{L C}}\right]\) of the RLC circuit, the current in the circuit reaches its maximum value. Then the circuit is said to be in electrical resonance. The frequency at which resonance takes place is called resonant frequency. Resonant angular frequency, ωr = \(\frac { 1 }{ \sqrt { LC } } \)
Question 18.
How will you define Q-factor?
Answer:
- Q factor is defined as the ratio of voltage across L or C to the applied voltage.
- Q – factor = \(\frac{\text { Voltage across } L \text { or } C}{\text { Applied Voltage }}\)
- Q factor = \(\frac{1}{R} \sqrt{\frac{L}{C}}\)
Question 19.
What is meant by wattles current?
Answer:
The component of current (IRMS sin φ), which has a phase angle of \(\frac { π }{ 2 }\) with the voltage is called reactive component. The power consumed is zero. So that it is also known as ‘Wattless’ current.
Question 20.
Give any one definition of power factor.
Answer:
Power factor is defined as
- Power factor = cos Φ = cosine of the angle of lead or leg.
- Power factor = \(\frac{R}{Z}=\frac{\text { Resistance }}{\text { Impedance }}\)
- Power factor = \(\frac{\text { True power }}{\text { Apparent power }}\)
Question 21.
What are LC oscillations?
Answer:
Whenever energy is given to a LC circuit, the electrical oscillations of definite frequency are generated. These oscillations are called LC oscillations. During LC oscillations, the total energy remains constant. It means that LC oscillations take place in accordance with the law of conservation of energy.
![]()
III. Long Answer Questions:
Question 1.
Establish the fact that the relative motion between the coil and the magnet induces an emf in the coil of
a closed circuit.
Answer:
1. In first experiment when bar magnet is placed close to the coil, magnetic lines pass through coil, the magnetic flux in coil increases and emf is induced hence electric current flows in the circuit.
2. At the same time when they recede away from one another magnetic flux decreases emf is induced in opposite direction. Current flows in opposite direction. So there is a deflection in the galvanometer.
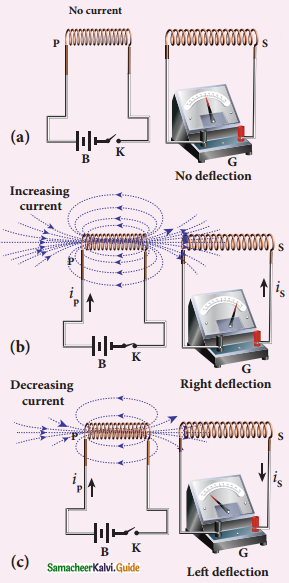
3. In second experiment, when the primary circuit is open, no electric current flows in it, magnetic flux linked with the secondary coil is zero.
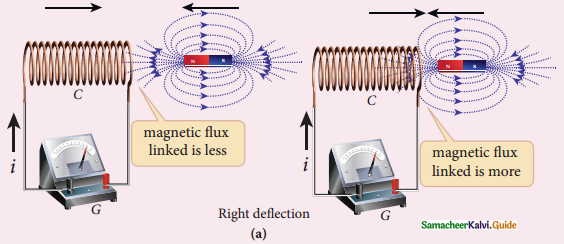
4. When primary circuit is closed, increasing current produce magnetic field. So magnetic flux linked with coil increases. This induced current in secondary coil.
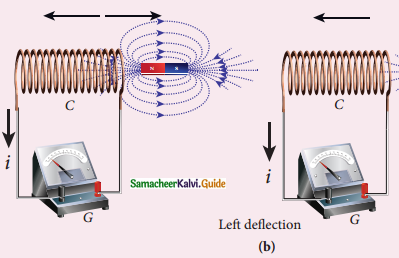
5. When primary circuit is broken, decreasing primary current induces current in secondary coil but in opposite direction. So there is a deflection in Galvanorneter.
Question 2.
Give an illustration of determining direction of induced current by using Lenz’s law.
Answer:
1. Move the bar magnet towards solenoid with north pole pointing solenoid.
2. When the Magnetic flux increases in the coil, induced current is produced, and the coil becomes magnetic dipole.
3. According to Lenz law, induced current opposes the movement of north pole towards coil.
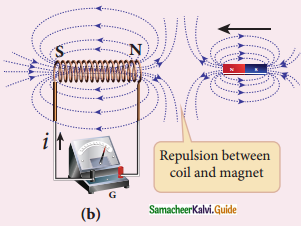
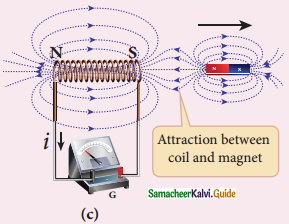
4. It is possible if end nearer to magnet become north pole, then it repels the north pole of magnet and oppose the movement of magnet.
5. The direction of induced current is found by the right hand thumb rule.
6. When a bar magnet is withdrawn, nearer end becomes south pole which attracts north pole of the bar magnet, opposing the receding motion of magnet.
7. Direction of induced current can be found from Lenz law.
![]()
Question 3.
Show that Lenz’s law is in accordance with the law of conservation of energy.
Answer:
Conservation of energy:
The truth of Lenz’s law can be established on the basis of the law of conservation of energy. According to Lenz’s law, when a magnet is moved either towards or away from a coil, the induced current produced opposes its motion. As a result, there will always be a resisting force on the moving magnet.
Work has to be done by some external agency to move the magnet against this resisting force. Here the mechanical energy of the moving magnet is converted into electrical energy which in turn, gets converted into Joule heat in the coil i.e., energy is converted from one form to another.
Question 4.
Obtain an expression for motional emf from Lorentz force.
Answer:
1. Consider a straight rod AB of length l in uniform magnetic field perpendicularly to plane of paper.
2. Let rod move with constant velocity \(\overrightarrow{\mathrm{v}}\) towards right side free electrons present in it also move with same \(\overrightarrow{\mathrm{v}}\) in \(\overrightarrow{\mathrm{B}}\)
3. The Lorentz force is \(\overrightarrow{\mathrm{F}}_{\mathrm{B}}\) = -e (\(\overrightarrow{\mathrm{v}}\) × \(\overrightarrow{\mathrm{B}}\) )
4. Due to electric field E , the coulomb force starts acting on free electrons along AB.
\(\overrightarrow{\mathrm{F}}_{\mathrm{B}}\) = -e\(\overrightarrow{\mathrm{E}}\)
5. Magnitude of \(\overrightarrow{\mathrm{E}}\) increasing as long as accumulation of electrons at the end A continues \(\overrightarrow{\mathrm{F}}_{\mathrm{E}}\) increases until equilibrium is reached.
6. At equilibrium,
\(\left|\overrightarrow{\mathrm{F}}_{\mathrm{B}}\right|=\left|\overrightarrow{\mathrm{F}}_{\mathrm{E}}\right|\)
\(|-e(\vec{v} \times \vec{B})|=|-e \quad \overrightarrow{\mathrm{E}}|\)
vB sin 90° = E
vB = E
7. The Potential difference is V = El
V = vBl
So, ε = Blv
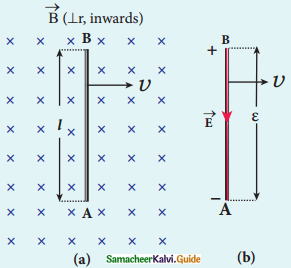
8. An emf is produced due to movement of rod, it is called as motional emf.
9. If A and B are connected by external circuit of resistance R, then the current \(i=\frac{\varepsilon}{R}=\frac{B l V}{R}\) flows in it.
10. Direction of current is found from right-hand thumb rule.
Question 5.
Give the uses of Foucault current.
Answer:
Though the production of eddy current is undesirable in some cases, it is useful in some other cases. A few of them are
- Induction stove
- Eddy current brake
- Eddy current testing
- Electromagnetic damping
1. Induction stove:
An induction stove is used to cook the food quickly and safely with less energy consumption. Below the cooking zone, there is a tightly wound coil of insulated wire. The cooking pan made of a suitable material is placed over the cooking zone.
When the stove is switched on, an alternating current flowing in the coil produces a high frequency alternating magnetic field which induces very strong eddy currents in the cooking pan. The eddy currents in the pan produce so much of heat due to Joule heating which is used to cook the food.
2. Eddy current brake:
This eddy current braking system is generally used in high-speed trains and roller coasters. Strong electromagnets are fixed just above the rails. To stop the train, electromagnets are switched on. The magnetic field of these magnets induces eddy currents in the rails which oppose or resist the movement of the train. This is Eddy’s current linear brake.
In some cases, the circular disc, connected to the wheel of the train through a common shaft, is made to rotate in between the poles of an electromagnet. When there is a relative motion between the disc and the magnet, eddy currents are induced in the disc which stop the train. This is Eddy current circular brake.
3. Eddy current testing:
It is one of the simple non-destructive testing methods to find defects like surface cracks and air bubbles present in a specimen. A coil of insulated wire is given an alternating electric current so that it produces an alternating magnetic field.
When this coil is brought near the test surface, eddy current is induced in the test surface. The presence of defects causes the change in phase and amplitude of the eddy current that can be detected by some other means. In this way, the defects present in the specimen are identified.
4. Electromagnetic damping:
The armature of the galvanometer coil is wound on a soft iron cylinder. Once the armature is deflected, the relative motion between the soft iron cylinder and the radial magnetic field induces eddy current in the cylinder. The damping force due to the flow of eddy current brings the armature to rest immediately and then the galvanometer shows a steady deflection. This is called electromagnetic damping.
![]()
Question 6.
Define self – inductance of a coil in terms of
(i) magnetic flux and
(ii) induced emf.
Answer:
- Let be the magnetic flux linked each turn of the coil of N turns, then the total flux linked with the coil NPB is proportional to the current i in the coil
NφB α i
NφB = Li ……………(1) - Self-inductance of a coil is defined as the flux linkage of the coil when 1 A current flows through it.
L = \(\frac{\mathrm{N} \Phi_{\mathrm{B}}}{i}\) If i = 1A then L = NφB - When the current i changes with time, an emf is induced in it. From Faradys law of electro magnetic induction, this self induced emf is given
ε = \(-d \frac{\left(\mathrm{N} \varphi_{\mathrm{B}}\right)}{d t}=-d \frac{(\mathrm{Li})}{d t}\)
Using equation (1)
L = \(\frac{-\varepsilon}{d i / d t}\) If di/dt = 1A.S-1 then L = -ε - Self inductance of coil is defined as opposing emf induced in the coil when the rate of change of current through the coil is 1As-1
Question 7.
How will you define the unit of inductance?
Answer:
Unit of inductance: Inductance is a scalar and its unit is Wb A-1 or V s A-1. It is also measured in henry (H).
1 H = 1 Wb A-1 = 1 V s A-1
The dimensional formula of inductance is M L2 T-2A-2.
If i = 1 A and NΦB = 1 Wb turns, then L = 1 H.
Therefore, the inductance of the coil is said to be one henry if a current of 1 A produces unit flux linkage in the coil.
If \(\frac { di}{ dt }\) = 1 As-1 and ε = -1 V, then L = 1 H.
Therefore, the inductance of the coil is one henry if a current changing at the rate of 1 A s-1 induces an opposing emf of 1 V in it.
Question 8.
What do you understand by the self-inductance of a coil? Give its physical significance.
Answer:
Self Inductance of coil:
1. Inductance or simply inductance of a coil is defined as the flux linkage of the coil when I A current flows through it.
2. Inductance of a coil is also defined as opposing emf induced in the coil when the rate of change of current through the is 1 As-1.
Physical Significance:
3. In translational motion, mass is measure of inertia, for rotational motion, moment of inertia is a measure of rotational inertia.
4. The inductance plays the same role in circuit as mass and moment of inertia play in mechanical motion.
5. When a circuit is switched on, the increasing current induces on emf which opposes the growth of current in circuit (Figure (a))
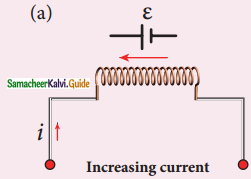
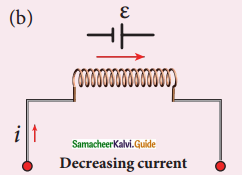
6. Induced emf e opposes the changing current i When circuit is broken, the decreasing current induces an emf in the reverse direction. This emf now opposes the decay of current (Figure (b))
7. Thus, inductance of the coil opposes any change in current and tries to maintain the original state.
Question 9.
Assuming that the length of the solenoid is large when compared to its diameter, find the equation for its inductance.
Answer:
1. Consider a long solenoid of length l and cross-sectional area A. Let n be the number of turns per unit length (1> n).
2. When the current i pass through solenoid, uniform magnetic field B is produced.
B = µ0ni
3. The magnetic field passes through each turn is
ΦB = \(\int_{A} \vec{B} \cdot d \vec{A}\) = BA cosθ = BA, Since θ = 0°
ΦB = (µ0 ni)A
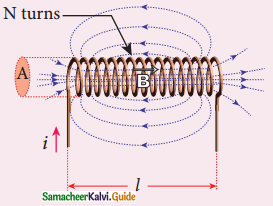
Self inductance of a long solenoid
4. Total magnetic flux of solenoid with N turns (N = nl)
NΦB = (nl)(µ0 ni) AB
NΦB = (µ0 n2 Al) i
5. we have L = µ0n2Al
6. Inductance depends on geometry of solenoid and medium present inside the solenoid.
7. For dielectric medium of µr
L = µn2Al (or)
L = µ0 µr n2 Al
Question 10.
An inductor of inductance L carries an electric current i. How much energy is stored while establishing the current in it?
Answer:
When current is established in circuit, inductance opposes the growth of current. So, work is done against this opposition by external agency. This work done is stored as magnetic potential energy.
Induced emf at any instant is
ε = -L\(\frac{d i}{d t}\)
Work done dW = -ε dq = -εidt
∴ dq = idt
Substituting for ε from first equation
ε = -L \(\frac{d i}{d t}\)
dw = -(-L \(\frac{d i}{d t}\)) i dt
dw = Li di
Total work done
W = ∫ dw = \(\int_{0}^{i}\)Li di = L\(\left[\frac{i^{2}}{2}\right]\)
W = \(\frac{1}{2}\) Li2
This work done is stored as magnetic potential energy
∴ UB = \(\frac{1}{2}\) Li2
Energy density is the energy stored per unit volume of space
UB = \(\frac{\mathrm{U}_{\mathrm{B}}}{\mathrm{Al}}\)
∴ Volume of solenoid = Al
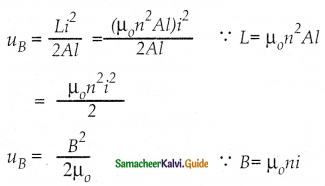
![]()
Question 11.
Show that the mutual inductance between a pair of coils is same (M12 = M21)
Answer:
Consider two coils placed close to each other, i1 is the electric current sent through coil 1 linked with coil 2.
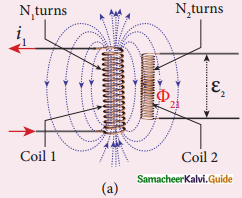
Let Φ21 be the magnetic flux linked with coil 2 of N2 due to coil 1
N2 Φ21 α i1
N2 Φ21 = M21 i1
M21 = \(\frac{\mathrm{N}_{2} \Phi_{21}}{i_{1}}\)
M21 is called mutual inductance of coil 2 with respect to coil 1. It is also called coefficient of mutual inductance.
If i1 = 1A then M21 = N2 Φ21
Mutual Inductance M21 is defined as flux linkage of coil 2 when 1 A current flows through coil 1.
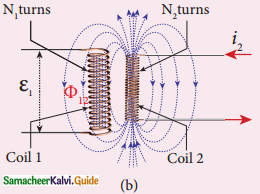
When i1 changes with time emf ε2 is induced in coil 2. From Faraday’s law of electromagnetic
induction
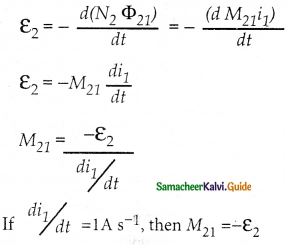
Mutual inductance M21 is defined as emf induced in coil 2 when rate of change of current through the coil I is 1 As-1
Similarly,
M12 = \(\frac{\mathrm{N}_{1} \Phi_{12}}{i_{2}}\) and
M12 = \(\frac{-\varepsilon_{2}}{d i_{2} / d t}\)
The mutual inductance is same ie M21 = M12 = M
The mutual inductance between two coils depends on size, shape, number of turns of the coils, relative orientation and permeability of the medium.
Question 12.
How will you induce an emf by changing the area enclosed by the coil?
Answer:
1. Consider a conducting rod of length l moving with velocity v towards left.
2. The whole arrangement is in uniform magnetic field \(\overrightarrow{\mathrm{B}}\), magnetic lines perpendicular to plane of the paper.
3. As the rod moves from AB to CD in time dt area enclosed by the loop and the magnetic flux through the loop decreases.
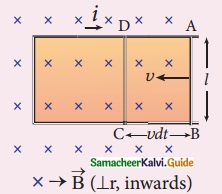
Induction of emf by changing the area enclosed by the loop
Change in magnetic flux in time dt is
dΦB = B × change in area
= B × Area ABCD
= Blv dt
(or) \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = Blv
The magnitude of induced emf.
ε = \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
ε = Blv
The emf is called motional Emf,
Direction of induced current is clockwise from Flemings Right hand rule.
Question 13.
Show mathematically that the rotation of a coil in a magnetic field over one rotation induces an alternating emf of one cycle.
Answer:
1. Consider a rectangular coil of N turns in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\)
2. Coil rotates with angular velocity ω about an axis in an anticlockwise direction perpendicular to the field.
3. At t = 0 plane of coil is perpendicular to the field so flux linked with the coil is Φm = BA
4. At t seconds coil is rotated through angle Φ flux is Φm cos ωt, component of Φm normal to the coil.
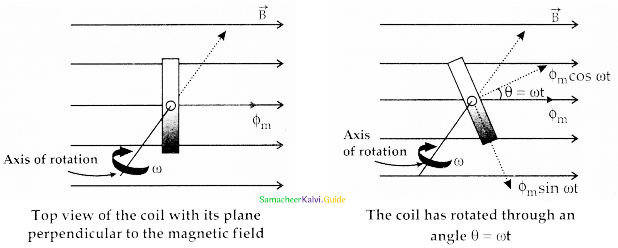
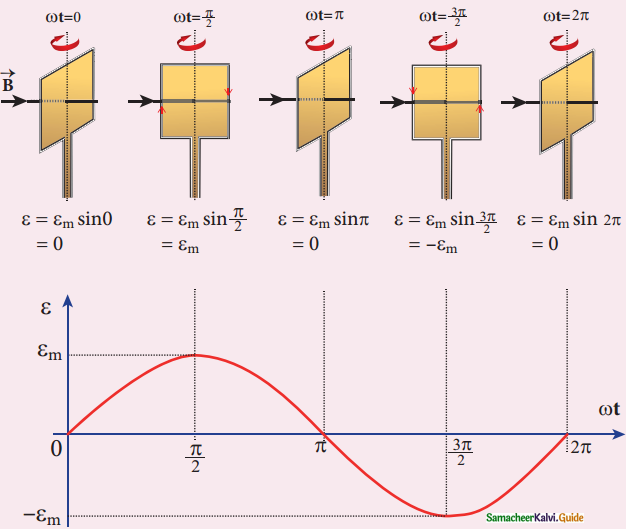
Variation of induced emf as a function ωt
According to Faraday’s law the ernf at any instant is
ε = –\(\frac{\mathrm{d}}{\mathrm{dt}}\) (N ΦB)
= –\(\frac{\mathrm{d}}{\mathrm{dt}}\) (N Φm cos ωt)
= -NΦm(-sin ωt) ω
= NΦm ω sin ωt
5. When the coil is rotated through 90°, sin ωt = 1.
6. The maximum induced emf is
εm = NΦm ω
εm = NBAω since Φm = BA
∴ Value of induced emf at any instant is
ε = εm sin ωt
The alternating current is given by i = Im sin ωt
Im = maximum value of induced current.
![]()
Question 14.
Elaborate the standard construction details of AC generator.
Answer:
Alternator consists of two major parts namely stator and rotor.
i) Stator:
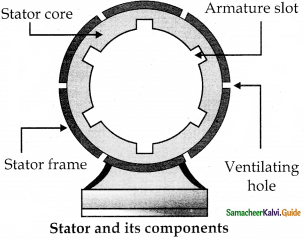
- The stationary part which has armature windings mounted in it, is called stator.
- This is outer frame used for holding stator core and armature windings in proper position. It provides best ventilation.
Stator core:
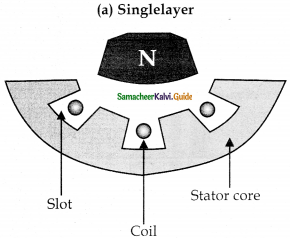
It is made up of iron or steel alloy. It is hollow cylinder and is laminated to minimize eddy current.
Armature winding:
- It is the coil, wound on slots, provided in the armature core.
- Two types are single layer winding and double layer winding.
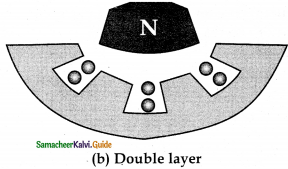
ii) Rotor:
1. Rotor contains magnetic field windings. Magnetic poles are magnetized by DC source.
2. Ends of field wings are connected to slip rings attached to rotor rotates.
3. Slip rings rotate along with the rotor.
4. Brushes are used which continuously slide over slip rings to maintain connection between DC source and windings.
5. Two types of rotors are
i) salient pole rotor.
ii) cylindrical pole rotor.
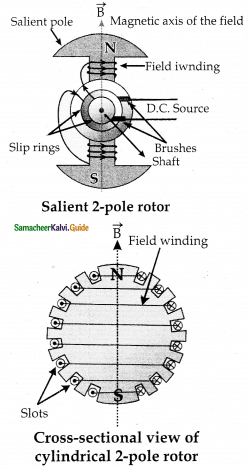
i) Salient pole rotator:
It has a number of projecting poles having their bases riveted to the rotor. It is used in low-speed alternators.
ii) Cylindrical pole rotor:
It consists of a smooth solid cylinder. The slots are cut on the outer surface of the cylinder along its length. It is suitable for very high-speed generator.
Question 15.
Explain the working of a single-phase AC generator with the necessary diagram.
Answer:
1. The loop PQRS is stationary and perpendicular to plane, when field windings are excited, magnetic field is produced around it.
2. Let field magnet be rotated in clockwise direction. Assume initial position is horizontal, direction of magnetic field is perpendicular to plane of loop PQRS Induced emf is zero. It is represented by O in the graph.
3. When rotates to 90°, magnetic field is parallel to PQRS, an induced emf becomes maximum. Direction of induced emf is given by Flemming’s right hand rule.
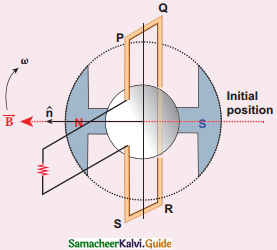
The loop PQRS ad field magnet in its initial position
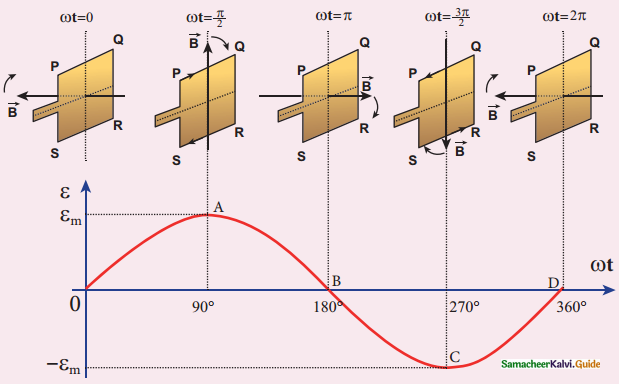
Variation of induced emf with respect to time angle
4. When rotates to 180°, field is perpendicular to PQRS, an induced emf is zero. It is represented by point B.
5. When rotates to 270°, field is parallel to PQRS, an induced emf is maximum but in reverse direction.
6. Current flows in SRQP. It is represented by point C.
7. On completion of 360°, field is perpendicular to PQRS, an induced emf is zero and noted by point D.
8. When field magenets complete one rotation, induced emf in PQRS finishes one cycle.
9. Frequency depends on speed of field magnet rotates.
![]()
Question 16.
How are the three different EMFs generated in a three-phase AC generator? Show the graphical representation of these three EMFs.
Answer:
1. In three-phase AC generator, the armature has 6 slots cut on its inner rim. Each slot is 60° away from one another. Six armature conductors mounted in these slots.
2. The conductors 1 and 4 joined in series to form coil 1.
The conductors 3 and 6 form coil 2.
The conductors 5 and 2 form coil 3.
3. These coils are rectangular and 120° apart from one another.
4. The initial position of field magnets is horizontal and direction is perpendicular to plane of coil 1.
5. When rotates from clockwise direction alternating emf in coil 1 begins a cycle from 0.
6. The corresponding cycle for in coil 2 starts at A after field magnet rotated through 120°.
7. So phase difference between ε1 and ε2 is 120°.
8. Similarly ε3 in coil 3 would begin its cycle at B after 240° from initial position.
9. Thus emfs produced in three-phase AC generator have 120° phase difference between one another.
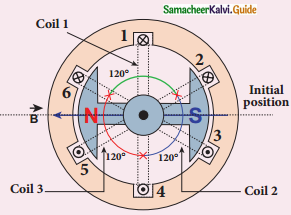
Construction of three – Phase AC generator
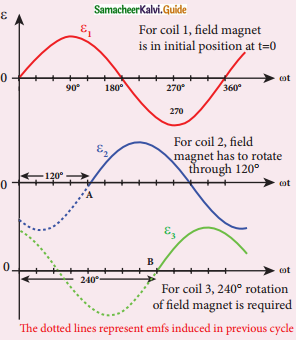
Variation of emfs ε1, ε2, and ε3 with time angle
Question 17.
Explain the construction and working of transformer.
Answer:
1. The principle of transformer is the mutual induction between two coils.
2. Two coils of high mutual inductance wound over the transformer core.
3. The core is laminated and made up of silicon steel.
4. Coils are insulated but magnetically linked via transformer core.
5. The coil across which alternating voltage is applied is called primary coil P.
6. Core and coil are kept in containers filled with suitable medium for insulation and cooling.
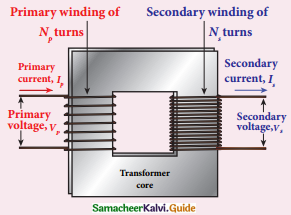
Construction of Transformer
Working:
1. If primary coil is connected with a.c input voltage the production of alternative magnetic flux linked with primary coil is linked with secondary coil.
2. As a result of flux change emf is induced in both coils.
3. Emf induced in primary coil is
νp = εp = -Np \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) ……………(1)
4. Emf induced in secondary coil is
εS = -NS \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
5. Np, NS is a number of turns in primary and secondary coil.
6. If secondary circuit is open εS = νS
νS = εS = -NS \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) ………………….(2)
7. From eqn (1) and (2)
\(\frac{v_{S}}{v_{p}}=\frac{N_{S}}{N_{P}}=K\) ………………(3)
p is voltage transformer ratio
8. For ideal transformer,
Input power vpip = Output power vsis
(ip, is are currents in Primary and secondary coil)
\(\frac{\mathrm{V}_{\mathrm{S}}}{\mathrm{V}_{\mathrm{P}}}=\frac{\mathrm{N}_{\mathrm{S}}}{\mathrm{N}_{\mathrm{P}}}=\frac{\mathrm{i}_{\mathrm{P}}}{\mathrm{i}_{\mathrm{S}}}\) ………..(4)
Step up transformer:
(i) If Ns > Np or K > I, Vs > Vp and Is < Ip
Voltage is increased, the current is decreased.
(ii) Step down transformer
Ns < Np or K< l, Vs < Vp and Is > Ip
Voltage is decreased, the current is increased.
Effeciency of a transformer,
η = \(\frac{\text { Output power }}{\text { Input power }}\) × 100%
![]()
Question 18.
Mention the various energy losses in a transformer.
Answer:
i) Core loss or Iron loss:
- Hysteresis loss and eddy current loss are known as core or Iron loss.
- When transformer core is magnetized and demagnetized repeatedly by a.c voltage Hysteresis loss takes place. It is minimized by silicon steel core.
- Alternating magnetic flux in core induce eddy current, due to flow of eddy current energy loss takes place. It is minimized by thin lamination of transformer core.
ii) Copper loss:
When current flows through core energy is dissipated due to Joule heating. It is a copper loss, it is minimized by using large-diameter wire.
iii) Flux leakage:
Flux leakage happens, when the magnetic lines of the primary coil are not completely linked with the secondary coil. Energy loss due to flux leakage is minimized by winding coil one over the other.
Question 19.
Give the advantage of AC in long-distance power transmission with an example.
Answer:
- When power is transmitting for long-distance a fraction of power is lost due to joule heating (I2R).
- This power loss can be tackled either by reducing current i or by reducing resistance R of a transmission line.
- At the transmitting point, voltage is increased and the current is decreased by a step-up transformer.
- This reduced current at high voltage reaches the destination without applicable loss.
- At the receiving point, voltage is decreased and current is increased by step down transformer.
Example 1:
2MW power is transmitted at 40Ω with 10 kV voltage
I = \(\frac{P}{V}=\frac{2 \times 10^{6}}{10 \times 10^{3}}\) = 200 A
Power loss = I2 R = (200)2 × 40 = 1.6 × 106 W
% of Power loss = \(\frac{1.6 \times 10^{6}}{2 \times 10^{6}}\) × 100% = 80%
Example 2:
When 2MW power at 40 Q is transmitted with 100 kV voltage.
I = \(\frac{P}{V}=\frac{2 \times 10^{3}}{100 \times 10^{3}}\) = 20 A
Power loss = I2 R = (200)2 × 40 = 0.016 × 106 W
% of power loss = \(\frac{0.016 \times 10^{6}}{2 \times 10^{6}}\) × 100%
= 0.8 × 100% = 80%
Question 20.
Find out the phase relationship between voltage and current in a pure inductive circuit.
Answer:
1. Consider a circuit containing pure inductor L across a.c. voltage source
2. υ = Vm sin ωt
Back emf ε = – L \(\frac{d i}{d t}\)
3. By applying kirchoff’s loop rule
ν + ε = 0
Vm sin ωt = L \(\frac{d i}{d t}\)
di = \(\frac{V_{m}}{L}\) sin ωt dt
Integrating both sides.
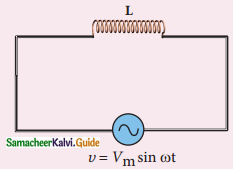
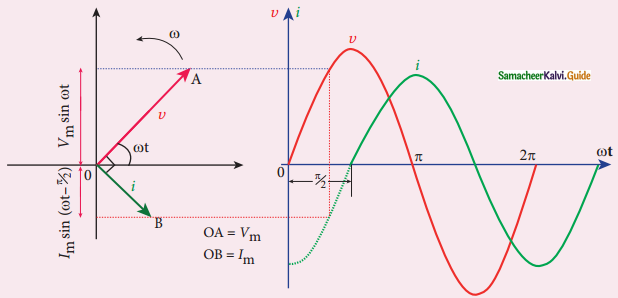
Phasor diagram and wave diagram for AC circuit with L.
i = \(\frac{V_{m}}{L}\) ∫ sin ωt dt
i = \(\frac{V_{m}}{L}\) (- cos ωt) + constant
i = \(\frac{V_{m}}{L}\) sin (ωt – π/2) or
i = Im sin (ωt – π/2)
where, \(\frac{V_{m}}{\omega L}\) = Im.
The peak value of a.c current lags behind voltage by π/2 in inductive circuit in phasor diagram. In wave diagram current lags voltage by 90°.
Im = \(\frac{V_{m}}{\omega L}\)
The quantity ωL is the resistance offered by inductor and called inductive reactance (χL)
χL = ωL
for ideal inductor χL = 0
![]()
Question 21.
Derive an expression for phase angle between the applied voltage and current in a series RLC circuit.
Answer:
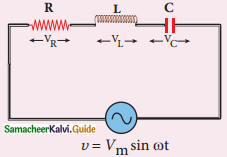
AC circuit containing R, L and C
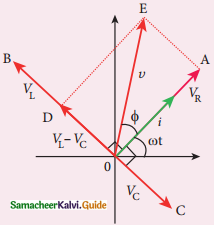
Phasor diagram for a series RLC – circuit when VL > VC
L(VL) leads I by π/2 and voltage across C(VC) lags I by π/2
Phasor diagram is drawn with the current.
The length of these phasors are
OI = Im, OA = ImR, OB = ImχL;
OC = ImχC
Vm2 = VR2 + (VL – VC)2

Special cases:
i) If χL> χC, (χL – χC) is positive and Φ is also positive.
∴ υ = Vmsin ωt; i = Im(sin(ωt – Φ))
ii) if χL < χC, (χL – χC) is negative and Φ is negative.
∴ υ = Vmsin ωt; i = Im(sin(wt + Φ))
Question 22.
Define inductive and capacitive reactance. Give their units.
Answer:
- Resistance offered by inductor is called inductive reactance (χL). Its unit is the ohm (Ω)
χL = ωL
If f = 0. χL = 0. - Resistance offered by capacitor is called capacitive reactance (χC). Its unit is also ohm (Ω)
χC = \(\frac{1}{\omega C}\)
If f = 0 ;
χC = \(\frac{1}{\omega C}\) = \(\frac{1}{2 \pi f C}=\frac{1}{0}\) = ∞
Question 23.
Obtain an expression for the average power of AC over a cycle. Discuss its special cases.
Answer:
In RLC circuit,
υ = Vm sin ωt and
i = Im sin (ωt + Φ)
where Φ is phase angle between υ and i
Instantaneous power is p = υi
= Vm Im sin ωt sin (ωt + Φ)
= Vm Im sin ωt (sin ωt cos Φ – cos ωt sin Φ)
P = Vm Im(cos Φ sin2ωt – sinωt cosωt sin Φ)
Average power over a cycle,
Pav = Vm Im cos Φ × \(\frac{1}{2}\)
= \(\frac{V_{m}}{\sqrt{2}} \frac{I_{m}}{\sqrt{2}}\) cos Φ
∴ Pav = VRMS IRMS P cos Φ
VRMS IRMS is apparent power cos Φ is power factor Average power of AC circuit is known as the true power of circuit.
Special Cases:
i) For pure resistive circuit phase angle is zero, cos Φ = 1
∴ Pav = VRMS IRMS
ii) For pure inductive or capacitive circuit cos (± π/2) = 0
∴ Pav = 0
iii) For RLC circuit Φ = \(\tan ^{-1}\left(\frac{X_{L}-X_{L}}{R}\right)\)
∴ Pav = VRMS IRMS
iv) For RLC circuit at resonance cos Φ = 1
∴ Pav = VRMS IRMS
![]()
Question 24.
Explain the generation of LC oscillation in a circuit containing an inductor of inductance L and a capacitor of capacitance C.
Answer:
LC Oscillations:
Whenever energy is given to a circuit containing a pure inductor of inductance L and a capacitor of capacitance C, the energy oscillates back and forth between the magnetic field of the inductor and the electric field of the capacitor. Thus the electrical oscillations of definite frequency are generated. These oscillations are called LC oscillations.
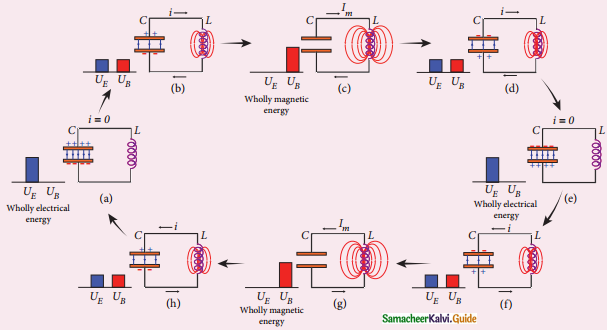
LC Oscillations
Generation of LC oscillations:
1. Let us assume that the capacitor is fully charged with maximum charge Qm at the initial stage. So that the energy store in the Qm capacitor is maximum and is given by UE = \(\frac{Q_{m}^{2}}{2 C}\)
2. As there is no current in the inductor, the energy stored in it is zero i.e., UE = 0. Therefore, the total energy is wholly electrical. (Figure (a)).
3. The capacitor now begins to discharge through the inductor that establishes current i in a clockwise direction. This current produces a magnetic field around the inductor and the energy stored in the inductor is given by
UE = \(\frac{\mathrm{Li}^{2}}{2}\)
As the charge in the capacitor decreases, the energy stored in it also decreases and is given by
UE = \(\frac{q^{2}}{2 C}\) total energy is the sum of electrical and magnetic energies. (Figure (b)).
4. When the charges in the capacitor are exhausted, its energy becomes zero i.e., UE = 0.
The energy is fully transferred to the magnetic field of the inductor and its energy is maximum.
5. This maximum energy is given by UE = \(\frac{\mathrm{Li}^{2}}{2}\) where Imis the maximum current flowing in the circuit. The total energy is wholly magnetic (Figure (c)).
6. Even though the charge in the capacitor is zero, the current will continue to flow in the same direction because the inductor will not allow it to stop immediately.
7. As a result of this, the capacitor begins to charge in the opposite direction. A part of the energy is transferred from the inductor back to the capacitor. The total energy is the sum of the electrical and magnetic energies. (Figure (d)).
8. (Fig. e) i = o the capacitor becomes fully charged in the opposite direction.
9. (Fig. f) The state of the circuit is similar to the initial state but the difference is that the capacitor is charged in opposite direction.
∴ Total energy = UE + UB.
10. As already explained, the process repeated in opposite direction (Fig. g and h). Finally alternating current flows in the circuit.
11. This process is repeated again and again to produce LC Oscillations.
Question 25.
Prove that the total energy is conserved during LC oscillations.
Answer:
- LC oscillation takes place in accordance with law of conservation of energy.
- Total energy U = UE + UB = \(\frac{q^{2}}{2 C}+\frac{1}{2} L i^{2}\)
Case (i):
When q = Qm and i = O
Total energy is U = \(\frac{\mathrm{Q}_{\mathrm{m}}^{2}}{2 \mathrm{C}}\) + o = \(\frac{\mathrm{Q}_{\mathrm{m}}^{2}}{2 \mathrm{C}}\)
Total energy is wholly electrical.
Case (ii):
When q = O i = Im total energy is
U = 0 + \(\frac{1}{2} L I^{2}\) = \(\frac{1}{2} L I^{2}\)
= \(\frac{L}{2} \times\left(\frac{Q^{2} m}{L_{C}}\right)\)
since Im = Qm ω
= \(\frac{Q_{m}}{\sqrt{L M}}\) = \(\frac{Q^{2} m}{2 C}\)
Total energy is wholly magnetic
Case (iii):
When charge = q, current = i
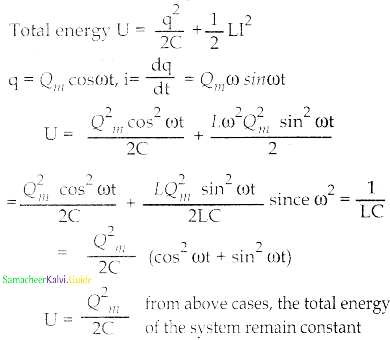
Question 26.
Compare the electromagnetic oscillations of the LC circuit with the mechanical oscillations of the block spring system qualitatively to find the expression for the angular frequency of LC oscillators mathematically.
Answer:
i) Qualitative treatment:
- Two forms of energy involved in LC oscillations. The’ are
1. electrical energy of capacitor.
2. Magnetic energy of inductor. - Angular frequency of oscillations of spring mass is
ω = \(\sqrt{\frac{k}{m}}\) where k → 1/C and m → L
ω = \(\frac{1}{\sqrt{L C}}\) …………..(1)
ii) Quantitative treatment:
Mechanical energy of spring mass system,
E = \(\frac{1}{2}\) mv2 + \(\frac{1}{2}\) kx2 …………(2)
m = \(\frac{d^{2} x}{d t^{2}}\) + kx = 0 ………………..(3)
x(t) = Xm cos(ωt + Φ)
Electromagnetic energy of LC system is
\(\mathrm{U}=\frac{Q_{m}^{2} \cos ^{2} \omega \mathrm{t}}{2 \mathrm{C}}+\frac{L \omega^{2} Q_{m}^{2} \sin ^{2} \omega \mathrm{t}}{2}\)
U = \(\frac{1}{2} L i^{2}+\frac{1}{2}\left(\frac{1}{C}\right) q^{2}\) = constant ……………(5)
Differentiate w.r.t to time
\(L \frac{d^{2} q}{d t^{2}}+\frac{1}{C} q=0\) ………………(6)
q(t) = Qm cos(ωt + Φ) ……………..(7)
current i(t)
i(t) = – Im sin (ωt + Φ) ……………..(8)
Angular frequency of LC oscillations
\(\frac{d^{2} q}{d t^{2}}\) = – Qm ω2 cos(ωt + Φ) ……………(9)
Substituting (7) and (9) in (6)
L[- Qm ω2 cos(ωt + ΦΠ)] + \(\frac{1}{C}\) Qm cos(ωt + Φ) = 0
Rearranging the terms, angular frequency of LC oscillation is
ω = \(\frac{1}{\sqrt{L C}}\)
![]()
IV. Numeric Problems:
Question 1.
A square coil of side 30 cm with 500 turns is kept in a uniform magnetic field of 0.4 T. The plane of the coil is inclined at an angle of 30° to the field. Calculate the magnetic flux through the coil.
Answer:
Given data:
Area A = 30 × 30 × 10-4 m2
n = 500
B = 0.4 T
Q = 90° – 30° = 60°
Φ = nBA cos Φ
=500 ×30 × 30 × 10-4 × 0.4 × cos60°
= 5 × 10 × 0.4× 9 × \(\frac{1}{2}\)
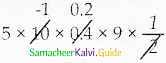
= 5 × 0.2 × 9 × 10
= 5 × 0.2 × 9 × 10-1
= 1.0 × 9 × 10-1
= 9 wb
Φ = 9 wb
Question 2.
A straight metal wire crosses a magnetic field of flux 4 mWb in a time of 0.4 s. Find the magnitude of the emf induced in the wire.
Answer:
Given data:
dΦ = 4 mWb = 4 × 10-3
dt = 0.4 s
induced emf ε =?
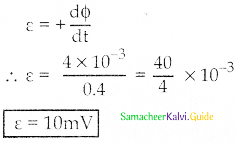
Question 3.
The magnetic flux passing through a coil perpendicular to its plane is a function of time and is given by φB = (2t3 + 4t2 + 8t + 8) Wb. If the resistance of the coil is 5Ω, determine the induced current through the coil at a time t = 3 second.
Answer:
Given data :
φB = (2t3 + 4t2 + 8t + 8) Wb
R = 5Ω
t = 3second
induced current i = ?
i = \(\frac{\varepsilon}{\mathrm{R}}\)
ε = \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
ε = \(\frac{d}{d t}\left(2 t^{3}+4 t^{2}+8 t+8\right)\)
ε = 6t2 + 8t + 8
at t = 3second,
ε = 6 × 32 × 8 × 3 + 8
ε = 54 + 24 + 8
ε = 86 V
∴ i = \(\frac{\varepsilon}{R}=\frac{86}{5}\) = 17.2 A
i = 17.2 A
Question 4.
A closely wound circular coil of radius 0.02 m is placed perpendicular to the magnetic field. When the magnetic field is changed from 8000 T to 2000 T in 6s, an emf of 44 V is induced in it. Calculate, the number of turns in the coil
Answer:
Given data:
radius r = 0.02 m
Q = 90° – 90° = 0°
B1 = 8000 T, B2 = 2000 T
dt = 68
ε = 68V
n = ?
ε = nA cos θ \(\frac{\mathrm{dB}}{\mathrm{dt}}\)
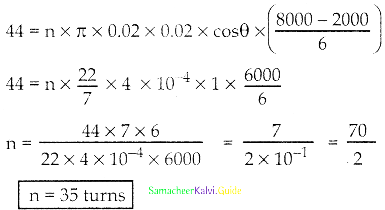
Question 5.
A rectangular coil of area 6 cm2 having 3500 turns is kept in a uniform magnetic field of 0.4 T. Initially, the plane of the coil is perpendicular to the field and is then rotated through an angle of 180°. If the resistance of the coil of 35Ω, find the amount of charge following through the coil.
Answer:
Given data:
Area A = 6 × 10-4 m2
n = 3500
B = 0.4 T
Q1 = 180°
R = 35Ω
amount of charge Q =?
Q = di.dt = \(\frac{\varepsilon}{R}\) dt
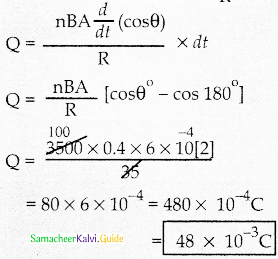
![]()
Question 6.
An induced current of 2.5 mA flows through a single conductor of resistance 1ooΩ. Find out the rate at which the magnetic flux is cut by the conductor.
Answer:
Given data:
Induced current i = 2.5 mA
i= 2.5 × 10-3 A
Resistance R = 100Ω
ε = \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
where ε = iR
∴ \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = iR = 2.5 × 10-3 × 100
= 250 × 10-3
= 250 mWbs-1
Question 7.
A fan of metal blades of length 0.4 m rotates normal to a magnetic field of 4 × 10-3 T. If the induced emf between the center and edge of the blade is 0.02 V, determine the rate of rotation of the blade.
Answer:
Given data:
length = 0.4 m
B = 4 × 10-3 T
ε = 0.02 V
The rate of rotation υ =?
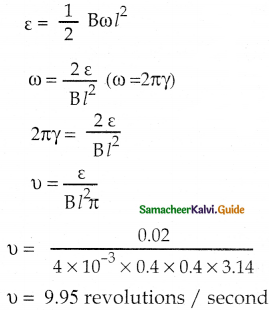
Question 8.
A bicycle wheel with metal spokes of 1m long rotates in Earth’s magnetic field. The plane of the wheel is perpendicular to the horizontal component of Earth’s field of 4 × 10-5 T. If the emf induced across the spokes is 31.4 mV, calculate the rate of revolution of the wheel.
Answer:
length l = 1 m
B = 4 × 10-5 T
E = 3.14 mV
= 3.14 × 10-3 V
The rate of revolution = ?
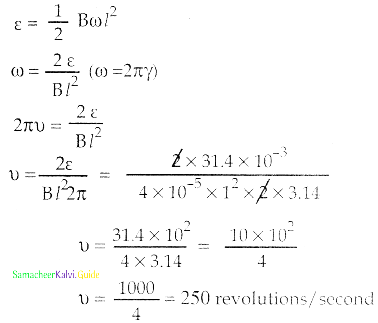
Question 9.
Determine the self-inductance of 4000 turn air-core solenoid of length 2 m and diameter 0.04 m.
Answer:
Given data:
n = 4000
l = 2m
diameter d = 0.04 m
radius r = 0.02 m
Self inductance L =?
L = µnA2 l
L = 4π × 10-7 × 4000 × π × 0.02 × 0.02 × 2
L = 16π × 10-1 × π × 8 × 10-4
L = 1262 × 10-5
L = 12.62 × 10-3 H
L = 12.62 mH
Question 10.
A coil of 200 turns carries a current of 4 A. If the magnetic flux through the coil is 6 x 10-5 Wb, find the magnetic energy stored in the medium surrounding the coil.
Answer:
Given data:
N = 200 turns
i = 4A
ΦB = 6 × 10-5 Wb
Magnetic energy UB =?
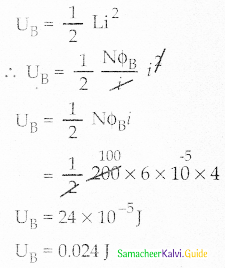
![]()
Question 11.
A 50 cm long solenoid has 400 turns per cm. The diameter of the solenoid is 0.04m. Find the, magnetic flux linked turn when it carries a current of IA.
Answer:
Given data:
Length of the solenoid, l = 50 cm = 50 × 10-2 m
No. of turns / cm = 400
For 50 cm, No. of turns N = 400 × 50 = 20,000
Diameter of the solenoid = 0.04 m
∴ Radius of the solenoid = 0.02 m
Current passing through the solenoid = 1 A
Area of the solenoid = πr²
= 3.14 × 0.02 × 0.02 m2
Formula :-
Magnetic flux, φ = µ0 n2 AIl

Question 12.
A coil of 200 turns carries a current of 0.4 A. If the magnetic flux of 4m Wb is linked with each turn of the coil, find the inductance of the coil.
Answer:
Given data:
N = 200
i = 0.4 A
ΦB = 4 mWb = 4 × 10-3 Wb
L = ?
NΦBi = Li
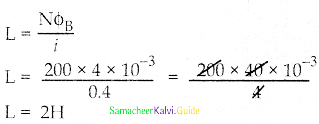
Question 13.
Two air core solenoids have the same length of 80 cm and same cross-sectional area 5 cm2. Find the mutual inductance between them if the number of turns in the first coil is 1200 turns and that in the second coil is 400 turns.
Answer:
Given data:
l = 80cm
A = 52 = 5 × 10-4 m2
= 80 × 10-2 m
turns = 1500 turns
n1 = \(\frac{1200}{0.8}\);
n1 = 1500turns
n2 = \(\frac{400}{0.8}\);
n2 = 500 turns
M = ?
Mn = μ0 n1 n2 A2 l
M = 4π × 10-7 × 1500 × 1500 × 5 × 10-4 × 0.8
M = 4π × 10-7 × 75 × 5 × 0.8
M = 3768 × 10-7 H
= 0.3768 × 10-3 H
M = 0.38 mH
Question 14.
A long solenoid having 400 turns per cm carries a current 2A. A 100 turn coil of cross-sectional area 4cm2 is placed co-axially inside the solenoid so that the coil is in the field produced by the solenoid. Find the emf induced in the coil if the current through the solenoid reverses its direction in 0.04 sec.
Answer:
Given data:
n1 = 400 turns/cm
∴ n1 = 4000 turns/m
n2 = 100
A2 = 4 × 10-4 m2
i = 1 m
di = 2-(-2) = 48
dt = 0.04 sec
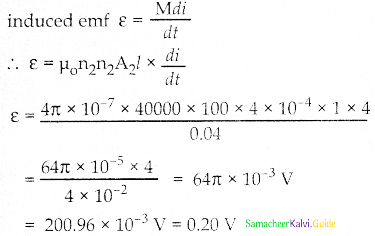
Question 15.
A 200 turn circular coil of radius 2 cm is placed co-axially within a long solenoid of 3 cm radius. If the turn density of the solenoid is 90 turns per cm, then calculate mutual inductance of the coil and solenoid.
Answer:
Given data:
r2 = 2 cm, n2 = 200
r1 = 3 cm
n1 = 90 turns/cm
n1 = 9000 turns/m
M =?
M = μ0 n1 n2 A2 l
M = 4π × 10-7 × 280 × 9000 × π × 4 × 10-4 × 1
M = 4π × 10-6 × 18 × 4π
M = 2.839.56 × 10-6 H
M = 2.839 × 10-3 H
M = 2.84 mH
![]()
Question 16.
The solenoids S1 and S2 are wound on an iron-core of relative permeability 900. The area of their cross-section and their lengths are the same and are 4 cm2 and 0.04 m respectively. If the number of turns in S1 is 200 and that in S2 is 800, calculate the mutual inductance between the solenoids. If the current in solenoid 1 is increased from 2A to 8A in 0.04 second. Calculate the induced emf in solenoid 2.
Answer:
Given data:
μr = 900
A2 = 4 × 10-4 m2
l = 0.04 m
n1 = 5000
n2 = 20,000
i1 =2A to i2 = 8A
dt = 0.048
M = ?
ε2 = ?
Solution:
M = μ0 μr n1 n2 A2 l
M = 4π × 10-7 × 900 × 5000 × 20000 × 4 × 10-4 ×0.04
M = 4π × 90 × 4 × 4 × 10-4
M = 18086 × 10-4H
M = 1.81 H
induced emf,
ε2 = M \(\frac{d i}{d t}\)
ε2 = 1.81 \(\left(\frac{(8-2)}{0.04}\right)\)
ε2 = \(\frac{1.81 \times 6}{4 \times 10^{-2}}\)
= 2.715 × 10-2 V
ε2 = 271.5 V
Question 17.
A step-down transformer connected to main supply of 220 V is used to operate 11V, 88W lamp. Calculate
(i) Transformation ratio and
(ii) current in the primary
Answer:
Given data:
Vp = 220 V, Ps = 88 W, Vs = 11 V

Question 18.
A 200 V/ 120 V step down transformer of 90% efficiency is connected to an induction stove of resistance 40Ω. Find the current drawn by the primary of the transformer.
Answer:
Given data:
Vp = 200 V
Vs = 120 V
η = 90% = \(\frac{90}{100}\) = 0.9
η = \(\frac{\text { output power }}{\text { input power }}\)
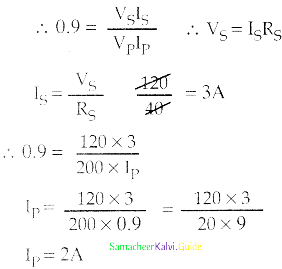
Question 19.
The 300 turn primary of a transformer has resistance 0.82 Q and the resistance of its secondary of 1200 turns is 6.2 Q. Find the voltage across the primary if the power output from the secondary at 1600 V is 32 kW. Calculate the power losses in both coils when the transformer efficiency is 80%.
Answer:
Given data:
NP = 300
NS = 1200
VS = 1600 V,
RP = 0.82Ω
RS = 6.2Ω
PS = 32 KW
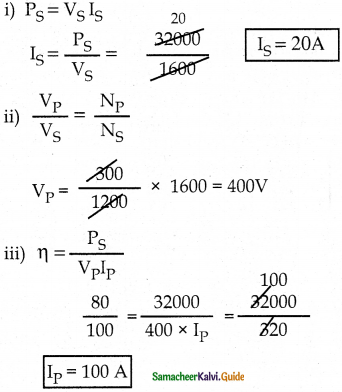
iv) Power loss in primary = (IP)2 × RP
= 100 × 1000 × 0.82
= 0.82 × 1000
= 8.2000 = 8.2 KW
v) Power loss in secondary = (IS)2 × RS
= 20 × 20 × 6.2
= 400 × 6.2
= 2480W = 2.48 KW
Question 20.
Calculate the instantaneous value at 60°, average value and RMS value of an alternating current whose peak vaue is 20A.
Answer:
Given data:
Im = 20 A Q = 60°
i) Instantaneous value of current
i = Im sin θ
= 20 × Sin 60°
= 20 × \(\frac{\sqrt{3}}{2}\)
= 10 × √3
= 10 × 1.732
i = 17.32 A
ii) Average value
Iav = 0.637 Im
Iav = 0.637 × 20
= 6.37 × 2
Iav = 12.74 A
iii) Irms = 0.707 Im
= 0.707 × 20
= 7.07 × 2
Irms = 14.14 A
![]()
V. Conceptual Questions:
Question 1.
A Graph between the magnitude of the magnetic flux linked with a closed-loop and time is given in the figure. Arrange the regions of the graph in ascending order of the magnitude of induced emf in the loop.
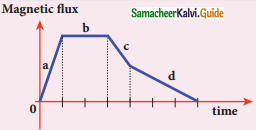
Answer:
induced emf ε = \(\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
i) Φ – t graph at ab is a straight line
∴ \(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = constant
∴ ε = -ve and constant
ii) Φ – t graph at bc, Φ is constant
∴ ε = 0
iii) Φ – t graph at cd is a straight line
\(\frac{\mathrm{d} \phi}{\mathrm{dt}}\) = constant
∴ ε = true and constant
iv) ab, bc, cd are ascending order of the magnitude of induced emf.
Question 2.
Using Lenz’s law, predict the direction of induced current in conducting rings 1 and 2 when the current in the wire is steadily decreasing.
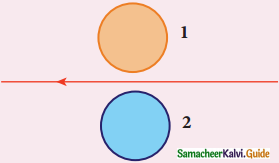
Answer:
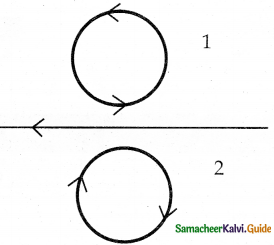
Current in the wire is steadily decreasing, so the induced current in rings 1 and 2 will flow in such a way that it oppose the decrease of current
- ring 1 is clockwise
- ring 2 is anti-clockwise
Question 3.
A flexible metallic loop abcd in the shape of a square is kept in a magnetic field with its plane perpendicular to the field. The magnetic field is directed into the paper normally. Find the direction of the induced current when the square loop is crushed into an irregular shape as shown in the figure.
Answer:
1. If a wire of irregular shape turns into a square loop then its area increases, so that the magnetic flux linked also increases
2. The induced current is in an anticlockwise direction, along abcd.
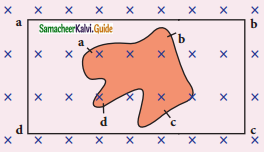
Question 4.
Predict the polarity of the capacitor in a closed circular loop when two bar magnets are moved as shown in the figure.
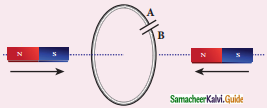
Answer:
- From Lenz’s law, the direction of the induced current is in a clockwise sense.
- This implies that plate A of the capacitor is at a higher potential than plate B
- B will be a negative plate while A will be a positive plate.
Question 5.
In a series LC circuit, the voltages across L and C are 180° out of phase. Is it correct? Explain.
Answer:
- Yes, it is correct
- In a pure inductor, the voltage leads the current by a phase angle of 90°.
- In a perfect capacitor, the voltage lags behind the current by a phase angle of 90°
- So, In series LC circuit, the voltage across L and C are 180° out of phase.
![]()
Question 6.
When does the power factor of a series RLC circuit become maximum?
Answer:
- Cos Φ is the power factor
- An RLC series circuit, the phase difference between voltage and current is zero when the circuit is at resonance.
- The power factor becomes maximum.
Part II:
Physics Guide Electromagnetic Induction and Alternating Current Additional Questions and Answers
I. Choose the best Answer:
Question 1.
A coil of area of cross section 0.5 m2 with 10 turns is in a plane which is perpendicular to an uniform magnetic field of 0.2 Wb/m2. The flux through the coil is –
(a) 100 Wb
(b) 10 Wb
(c) 1 Wb
(d) zero
Answer:
(c) 1 Wb
Hint:
Φ = NBA cos θ
= 10 x 0.2 x 0.5 x cos 0° = 1 Wb
Question 2.
What happens to the current in a coil while alternating a magnet inside it?
a) Increase
b) decreases
c) Remains constant
d) Reverse
Answer:
a) Increases
Question 3.
A wire of length 1 m moves with a speed of 10 ms-1 perpendiculars to a magnetic field. If the emf induced in the wire is 1 V, the magnitude of the field is-
(a) 0.01 T
(b) 0.1 T
(c) 0.2 T
(d) 0.02 T
Answer:
(b) 0.1 T
Hint:
ε = Blv
⇒ B = \(\frac { ε }{ lv }\) = \(\frac { 1 }{ 1 × 10 }\) = 0.02 T
Question 4.
If a conductor 0.2m long moves with a velocity of 0.3m/s in the magnetic field of 5T. Calculate the emf induced
a) 0.3 V
b) 0.03 V
c) 30 V
d) 3 V
Answer:
a) 0.3 V
Solution:
emf = Blv = 5 × 0.2 × 0.3 = 0.3 V
Question 5.
A coil of cross-sectional area 400 cm2 having 30 turns is making 1800 rev/min in a magnetic field of IT. The peak value of the induced emf is-
(a) 113 V
(b) 226 V
(c) 339 V
(d) 452 V
Answer:
(b) 226 V
Hint:
εm = NBA ω = 30 x 1 x 400 x 10-4 x 30 x 2π = 226 V
![]()
Question 6.
An electric generator consists of a 10-turn square wire loop of a side 50cm. The loop is turned so as to produce 50 Hz A.C. How strong must the magnetic field be for the peak output voltage to be 300V?
a) 2.4 T
b) 0.417 T
c) 2.62 T
d) 0.382 T
Answer:
d) 0.382 T
Question 7.
By accelerating magnet inside the coil current in it _____
a) increases
b) decreases
c) remains constant
d) reverse
Answer:
a) increases
Question 8.
When a direct current ‘i’ is passed through an inductance L, the energy stored is-
(a) Zero
(b) Li
(c) \(\frac { 1 }{ 2 }\) Li2
(d) \(\frac {{ L }^{ 2 }}{2i}\)
Answer:
(c) \(\frac { 1 }{ 2 }\) Li2
Question 9.
In an LCR series circuit, the voltage across each component L, C, and R is 50V. The voltage across the LC combination will be
a) 50 V
b) 0 V
c) 50 V
d) 100 V
Answer:
b) 0 V
Solution:
V = (ωL – \(\frac{1}{\omega_{C}}\)) Irms
= ωLIrms – \(\frac{1}{\omega_{C}}\)Irms
= 50 – 50 = 0
Question 10.
In AC circuit with inductance and capacitance are joined in series, current is found to be maximum when the value of inductance is 0.5 H and capacitance is 8 μF. The angular frequency of applied alternating voltage will be______
a) 400 Hz
b) 5000 Hz
c) 2 × 105 Hz
d) 300 Hz
Answer:
d) 500 Hz
Solution:
ω = \(\frac{1}{\sqrt{\mathrm{LC}}}\) = \(1 / \sqrt{0.5 \times 8 \times 10^{-6}}\)
ω = 500 Hz
![]()
Question 11.
AC supply gives 30V which passes through a 10ω resistance. The power dissipated in it is _______.
a) 90√2 W
b) 90 W
c) 45√2 W
d) 45 W
Answer:
b) 90 W
Solution:
P = \(\frac{V^{2}}{R}=\frac{30^{2}}{10}\) = 90 W
Question 12.
In an a.c circuit, an alternating voltage e = 200√2 sin 100t volts is connected to a capacitor of capacity 1 μF. The RMS value of the current in the circuit is
a) 10 mA
b) 100 mA
C) 200 mA
d) 20 mA
Answer:
d) 20 mA
Solution:
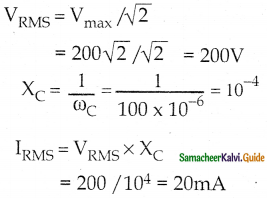
Question 13.
In an a.c circuit, the emf and current at any instant are e = E0 sin ωt, i = I0 sin ωt – Ø Average power is given by
a) E0 I0/2
b) (E0 I0/2) sin Φ
c) (E0 I0/2) cos Φ
d) E0 I0
Answer:
c) (E0 I0/2) cos Φ
Solution:
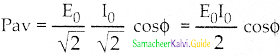
Question 14.
AC power is transmitted from a powerhouse at a high voltage as-
(a) the rate of transmission is faster at high voltages
(b) it is more economical due to less power loss
(c) power cannot be transmitted at low voltages
(d) a precaution against theft of transmission lines
Answer:
(b) it is more economical due to less power loss
Question 15.
What is the maximum value of inductance L for which the current is maximum in LCR circuit with C = 10 μF and ω = 1000 s-1
a) 1 mH
b) cannot calculate
c) 10 mH
d) 100 mH
Answer:
d) 100 mH
Solution:
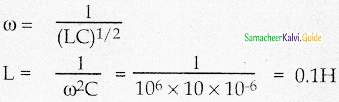
![]()
Question 16.
The primary winding of a transformer has 500 turns, whereas its secondary has 5000 turns. Primary is connected to a.c supply of 20V, 50Hz. The secondary will have an output of
a) 2 V, 5 Hz
b) 200 V, 500 Hz
c) 2 V, 50 Hz
d) 200 V, 50 Hz
Answer:
d) 200 V, 50 Hz
Solution:
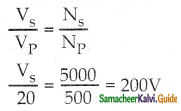
Question 17.
A step-up transformer operates on a 230 V line and supplied a load of 2A. The ratio of primary and secondary wings is 1:25. The current in primary is_______
a) 25 A
b) 50 A
c) 15 A
d) 12.5 A
Answer:
b) 50 A
Solution:
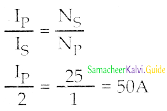
Question 18.
If N is the number of turns in a coil, the value of self-inductance varies as-
(a) N°
(b) N
(c) N2
(d) N-2
Answer:
(c) N2
Hint:
According to self-inductance of the long solenoid
L = \(\frac{\mu_{0} \mathrm{N}^{2} \mathrm{A}}{l}\)
⇒ L ∝ N2
Question 19.
A solenoid has n turns. Its coefficient of an inductance L varies with n as
a) L α n
b) L α n2
c) L α n-1
d) L α n
Answer:
b) L α n2
Question 20.
What is the coefficient of mutual inductance when magnetic flux charges by 2 × 10-2 Wb, one’s change in current is 0.01 A
a) 2 H
b) 3 H
c) 1/2 H
d) zero
Answer:
a) 2 H
Solution:
E = M\(\frac{d I}{d t}\) = 2 × 10-2 × 0.01 = 2
![]()
Question 21.
The phase difference between VL and VC in series RLC circuit.
a) 2π
b) \(\frac{\pi}{2}\)
c) \(\frac{2 \pi}{3}\)
d) π
Answer:
d) π
Question 22.
The quantity that remains unchanged in a transformer is-
(a) voltage
(b) current
(c) frequency
(d) none of these
Answer:
(c) frequency
Question 23.
The direction of the induced current is such that opposes the very cause that has produced it. This is the law of
a) Lenz
b) Faraday
c) Kirchoff
d) Fleming
Answer:
a) Lenz
Question 24.
Which one is correct?
a) Self-inductance is directly proportional to the current flowing through the coil
b) Self-inductance is directly proportional to the length
c) Self-inductance is directly proportional to its area of cross-section
d) Self-inductance is inversely proportional to the area of cross-section
Answer:
c) Self-inductance is directly proportional to its area of cross-section
Question 25.
A coil has a self-inductance of 0.04 H. The energy required to establish a steady-state current of 5 A in it is-
(a) 0.5 J
(b) 1.0 J
(c) 0.8 J
(d) 0.2 J
Answer:
(a) 0.5 J
![]()
Question 26.
A 50 mH coil carries a current of 4 amp. The energy stored in joule is_______
a) 0.4 J
b) 4.0 J
c) 0.8 J
d) 0.04 J
Answer:
a) 0.4J
Solution:
U = \(\frac{1}{2}\) Li2
= \(\frac{1}{2}\) × 50 × 10-3 × 45 × (4)2
Question 27.
If the angular speed of rotation of an armature of AC generator is doubled, the induced emf will be _______
a) same
b) doubled
c) halved
d) quadrupled
Answer:
b) doubled
Question 28.
Faraday’s law of electromagnetic induction is related to _______
a) law of conservation of charge
b) law of conservation of energy
c) Third law of Newton
d) law of conservation of angular momentum
Answer:
b) law of conservation of energy
Question 29.
The rms value of an alternating current, which when passed through a resistor produces heat three times of that produced by a direct current of 2 A in the same resistor, is-
(a) 6 A
(b) 3 A
(c) 2 A
(d) 2√3 A
Answer:
(d) 2√3 A
Hint:
\({ I }_{ rms }^{ 2 }\)R = 3(22R) (or) Irms = 2√3 A
Question 30.
RMS voltage and frequency of V = 230 sin (314t) A.C. source.
a) 162.6 V, 50 Hz
b) 230 V, 50 Hz
c) 230 V, 60 Hz
d) 162.6 V, 25 Hz
Answer:
d) 162.6 V, 25 Hz
![]()
Question 31.
From the reactance and frequency graph value of the inductance of given above the inductor is
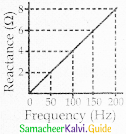
a) 3.18 × 10-14 H
b) 1/100π H
c) 50π H
d) 6.37 × 10-3 H
Answer:
d) 6.37 × 10-3 H
Question 32.
The impedance of a circuit consists of 3 Ω resistance and 4 Ω resistance. The power factor of the circuit is
(a) 0.4
(b) 0.6
(c) 0.8
(d) 1.0
Answer:
(b) 0.6
Hint:
tan Φ = \(\frac { 4 }{ 3 }\).
Power factor = cos Φ = \(\frac { 3 }{ 5 }\) = 0.06
Question 33.
Calculate the Q factor of RLC circuit if L = 80 µH, C = 2000 pF and R = 50Ω
a) 40
b) 400
c) 4
d) 0.4
Answer:
c) 4
Solution:
Q = \(\frac{1}{R} \sqrt{\frac{L}{C}}=\frac{1}{50} \sqrt{\frac{80 \times 10^{-6}}{200 \times 10}}\) = 4
Question 34.
The average power dissipation in pure (Ideal) inductor is
a) \(\frac{1}{2}\) Li2
b) 2 Li2
c) \(\frac{1}{2}\) Li2
d) zero
Answer:
d) zero
Question 35.
In an AC circuit, Resonance is obtained when
a) Z = R
b) Z = ωL – (1/ωC)
c) L=R
d) None
Answer:
a) Z = R
![]()
Question 36.
Change of current of 1 As-1 causes emf of 1V to be equal to______
a) 1 H
b) 1 V m-1
c) 1 Am
d) 1 J
Answer:
d) 1 H
Question 37.
In an AC circuit with voltage V and current I, the power dissipated is-
(a) VI
(b) \(\frac { 1 }{ 2 }\) VI
(c) \(\frac { 1 }{ √2 }\) VI
(d) depends on the phase difference between I and V
Answer:
(d) depends on the phase difference between I and V
Question 38.
A metallic ring is attached to wall of room. When north pole of magnet is brought near ring induced current in ring is
a) zero
b) clockwise
c) anticlockwise
d) infinite
Answer:
c) anticlockwise
Question 39.
In a series LCR circuit, R = 10 Ω and the impedance Z = 20 Ω. Then the phase difference between the current and the voltage is-
(a) 60°
(b) 30°
(c) 45°
(d) 90°
Answer:
(c) 60°
Hint:
cos Φ = \(\frac { R }{ Z }\) = \(\frac { 10 }{ 20 }\) = \(\frac { 1 }{ 2 }\)
⇒ Φ = 60°
Question 40.
Which of the following effects does an alternating current shows
a) Chemical effect
b) magnetic effect
c) heating effect
d) all the above
Answer:
c) heating effect
Question 41.
In the AC circuit the rms value of Irms is related to peak current I0 by the reaction
a) Irms = 1 I0
b) Irms = (1/√2) I0
c) Irms = 2 I0
d) Irms = π2I0
Answer:
b) Irms = (1/√2) I0
Question 42.
Match the following:
| i. Faraday’s law | a. conservation of energy |
| ii. Lenz law | b. Electromagnetic Induction |
| iii. Transformer | c. Right-hand rule |
| iv. Induced current | d. ε = – dΦ / dt |
a) i – a ii – d iii – c iv – b
b) i – c ii – a iii – d iv – b
c) i – d ii – a iii – b iv – c
d) i – a ii – d iii – b iv – c
Answer:
c) i-d, ii-a, iii-b, iv-c
Question 43.
The wattless circuit is obtained when the phase difference between virtual voltage and virtual current is
a) 90°
b) 45°
c) 80°
d) 60°
Answer:
a) 90°
![]()
II. Choose the Wrong statement:
Question 1.
Tick out the wrong statement:
a) An emf can be induced between the ends of a straight conductor by moving it through a uniform magnetic field.
b) The self-induced emf produced by changing the current in a coil always tends to decrease the current.
c) inserting an iron core in a coil increases the coefficient of self-inductance.
d) According to Lenz’s law direction of induced current oppose the flux change that causes it.
Ans :
b) The self-induced emf produced by changing the current in a coil always tends to decrease the current.
Question 2.
Tick out the wrong statement:
a) Inductor is used to store energy in a magnetic field when electric current flows through it,
b) According to Faraday’s law, an emf is induced in a conductor when magnetic flux passing through it.
c) Self-inductance is that current passing through coil changes with time emf is induced in neighbouring coil
d) The work done is stored as magnetic potential energy in the inductor.
Answer:
c) Self-inductance is that current passing through coil changes with time emf is induced in neighbouring coil.
Question 3.
Tick out the wrong one:
a) Changing the magnetic field B
b) Changing area A
c) Changing the orientation of the coil Q
d) Changing mass of the rod
Answer:
d) Changing mass of the rod
![]()
III. Assertion and Reason:
Question 1.
Assertion (A):
Emf is produced due to the movement of the rod it is often called motional emf.
Reason (R):
When the rod moves, free electrons in it also moves with the same velocity in B
a) A and R are correct R is the correct explanation of A
b) A and R arc correct But R is not the correct explanation of A
c) A is correct R is wrong
d) A is the wrong R is correct
Answer:
a) A and R are correct R is the correct explanation of A.
Question 2.
Assertion (A):
Three-phase generator produce higher output than single-phase generator
Reason (R):
Three-phase transmission is very cheaper.
a) A and R are correct R is the correct explanation of A
b) A and R are correct But R is not the correct explanation of A
c) A is correct R is wrong
d) A is the wrong R is correct
Answer:
b) A and R are correct But R is not the correct explanation of A
Question 3.
Assertion (A):
Alternating voltage and current in inductor system is V = Vm sin ωt and i = 1m sin(ωt – π/ 2)
Reason (R):
Current lags behind applied voltage by π/2
a) A and R are correct R is the correct explanation of A
b) A and R are correct But R is not the correct explanation of A
c) A is correct R is wrong
d) A is the wrong R is correct
Answer:
a) A and R are correct R is the correct explanation of A
![]()
IV. Fill in the blanks:
Question 1.
Condition for Resonance in RLC circuit is ______.
Answer:
χL = χC
Question 2.
Efficiency range of transformer is _______.
Answer:
96 – 99%
Question 3.
Energy stored in capacitor is ________.
Answer:
VE = ((Qm)2 / 2C)
Question 4.
Energy stored in the inductor is ______.
Answer:
VB = Li2/2
Question 5.
The magnification of vo1tae at series resonance is _______
Answer:
Q factor
![]()
V. Two Mark Questions:
Question 1.
Define magnetic flux
Answer:
The magnetic flux through an area A in a magnetic field is defined as the number of magnetic field lines passing through that area.
ΦB = ∫A \(\overrightarrow{\mathrm{B}}\) . d \(\overrightarrow{\mathrm{A}}\) = BA cos θ
Question 2.
Write down the drawbacks of Eddy currents.
Answer:
When eddy currents flow in the conductor, a large amount of energy is dissipated in the form of heat. The energy loss due to the flow of eddy current is inevitable but it can be reduced to a greater extent with suitable measures. The design of the transformer core and electric motor armature is crucial in order to minimise the eddy current loss.
To reduce these losses, the core of the transformer is made up of thin laminas insulated from one another while for electric motor the winding is made up of a group of wires insulated from one another. The insulation used does not allow huge eddy currents to flow and hence losses are minimized.
Question 3.
What is an inductor?
Answer:
Inductor is a device used to store energy in a magnetic field when an electric current flows through it.
Question 4.
Define self-inductance in terms of flux.
Answer:
Self-inductance of a coil is defined as the flux linkage of the coil when 1 A current flows through it
L = \(\frac{\mathrm{N} \Phi_{\mathrm{B}}}{i}\)
Question 5.
Define mutual inductance in terms of emf and current.
Answer:
Mutual inductance M21 is also defined as the opposing emf induced in coil 2 when the rate of change of current through coil 1 is 1 As-1.
M12 = \(\frac{-\varepsilon_{1}}{d i_{2} / d t}\)
![]()
Question 6.
Define Mutual Inductance.
Answer:
Mutual inductance is defined as opposing emf induced in the coil when the rating of change of current through another coil.
Question 7.
Define the unit of mutual Inductance.
Answer:
The mutual inductance between two coils is said to be one henry if a current of 1A in coil 1 produces unit flux linkage in coil 2.
Question 8.
Define the principle of Transformer.
Answer:
The principle of transformer is mutual induction between two coils. When electric current passing through a coil changes with time, an emf is induced in neighboring coil.
Question 9.
Define the Efficiency of Transformer.
Answer:
The ratio of output power to input power is the efficiency of the transformer.
η = \(\frac{\text { Output power }}{\text { Input power }}\)
The efficiency range is 96 – 99%
Question 10.
What is alternating voltage?
Answer:
An alternating voltage is a voltage which changes polarity at regular interval of time and the direction of the resulting alternating current also changes accordingly.
![]()
Question 11.
What is sinusoidal alternating voltage?
Answer:
If the waveform of the alternating voltage is a sine wave, then it is known as sinusoidal alternating voltage.
ν = Vm sin ωt.
Question 12.
Using Lenz’s law, predict the direction of induced current in conducting rings 1 and 2 when the current in the wire is
(i) steadily decreasing, and
(ii) steadily increasing.
Answer:
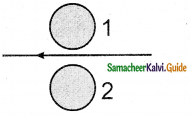
(i) 1f the current is steadily decreasing inducing current will be in a direction so as to oppose the decreasing magnetic flux according to Lenz law. Hence the direction of current is anticlockwise in the ring I and clockwise ring 2.
(ii) If the current is steadily increasing the induced current with the flow in such a way the direction of current is clockwise in ring 1 and anticlockwise in ring 2.
Question 13.
What is meant by sinusoidal alternating voltage?
Answer:
If the waveform of the alternating voltage is a sine wave, then it is known as sinusoidal alternating voltage, which is given by the relation.
υ = Vm sin ωt
Question 14.
Define power in AC circuit
Answer:
Power of a circuit is defined as the rate of consumption of electric energy in that circuit.
Question 15.
What is ‘wattfull current’?
Answer:
- Current component IRMS cos φ is the active component.
- Power consumed by current is VRMS IRMS cos φ. It is known as a wattful current.
![]()
Question 16.
Write any three definitions of power factor.
Answer:
- Power factor = cos φ is = cosine of angle of lead or lag
- Power factor = \(\frac{R}{Z}=\frac{\text { Resistance }}{\text { Impedance }}\)
- Power factor = \(\frac{\mathrm{VI} \cos \phi}{\mathrm{VI}}=\frac{\text { True power }}{\text { Apparent power }}\)
VI. Three Mark Questions:
Question 1.
List out the importance of Electromagnetic induction.
Answer:
- The application of electromagnetic induction is almost everywhere in the present life.
- Right from home appliances to huge factories, satellite communication all need electricity for their operation.
- So electric generators and transformers function on electromagnetic induction.
- Sophisticated human life would not be possible without the discovery of electromagnetic induction.
Question 2.
What are the drawbacks of eddy current?
Answer:
- When an eddy current flows in the conductor, a large amount of heat is dissipated in the form of heat.
- This can be reduced by suitable measures.
- The design of the transformer core and the electric motor armature is crucial in order to minimize the eddy current loss.
- To reduce this loss, the core of the transformer is made up of laminas insulated from one another.
- Electric motor winding is made up of a group of wires insulated from one another. The insulation does not allow eddy current to flow.
Question 3.
Write down the applications of the series RLC resonant circuit.
Answer:
RLC circuits have many applications like filter circuits, oscillators, and voltage multipliers, etc. An important use of series RLC resonant circuits is in the tuning circuits of radio and TV systems. The signals from many broadcasting stations at different frequencies are available in the air. To receive the signal of a particular station, tuning is done.
Question 4.
What are the advantages of the three-phase generator?
Answer:
- Three-phase produce a high power output
- For the same capacity, the three-phase alternator is small in size.
- It is cheaper. A relatively thinner wire is sufficient for transmission.
![]()
Question 5.
What is the mean or Average value of AC? Derive it.
Answer:
The average value of alternating current is defined as the average of all values of current over the positive or negative half cycle.
\(I_{a v}=\frac{\text { Area of }+\text { +ve half cycle }(\text { or }) \text { -ve half cycle }}{\text { Base length of half cycle }}\)
Let i be mid ordinate of that strip
Area of elementary strip = i dθ
Area of +ve half – cycle = \(\int_{0}^{\pi}\) idθ = \(\int_{0}^{\pi}\) Im sinθ dθ
= Im \([-\cos \theta]_{\mathrm{o}}^{\pi}\) = Im [cos π – cosθ]
= 2 Im
Average value of AC, Iav = \(\frac{2 \mathrm{I}_{\mathrm{m}}}{\pi}\)
Iav = 0.637 Im
For negative half -cycle Iav = – 0.637 Im
Question 6.
How to draw phasor diagram in AC
Answer:
- Length of line segment equals to peak value
- Vm or Im of alternating voltage.
- Its angular velocity ω is equal to the angular frequency.
- The projection of phasor on any vertical axis gives the instantaneous value of alternating voltage or current.
- The angle between phasor and axis of reference indicates the phase of alternating voltage.
Question 7.
Write three examples of power factor.
Answer:
- Power factor = cos 0° = 1 for pure resistive circuit because the phase angle p between voltage and current is zero.
- Power factor = cos(±π/2) = 0 for the purely inductive or capacitive circuit, because the phase angle between voltage and current is ±π/2
- Power factor lies between 0 and I for a circuit having R, L, and C in varying proportions.
Question 8.
Write the analogies between electrical and mechanical quantities.
Answer:
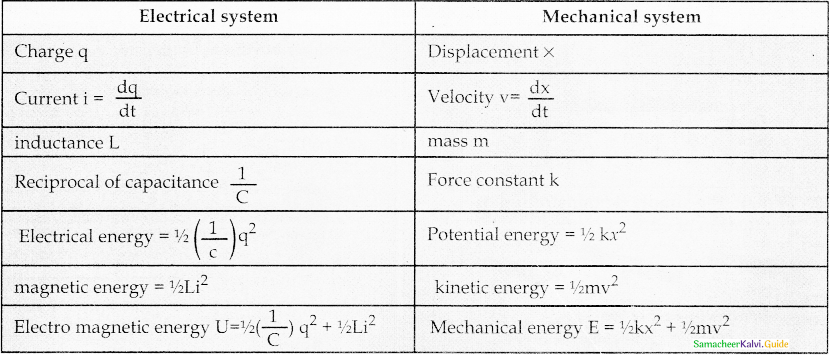
![]()
VII. Five Mark Questions:
Question 1.
Explain the first illustration of Lenz’s law and find the direction of induced current.
Answer:
1. Consider a uniform magnetic field, Field lines represented by (x).
2. A rectangular metallic frame ABCD is placed in this magnetic field its plane ⊥ to B.
3. If arm AB slides to our right side, a number of lines passing through ABCD increases and current is induced.
4. By lenz’s law induced current oppose this flux increases and try to reduce it by producing another magnetic field pointing outwards.
5. Magnetic loops of the induced field are represented by circle. Direction of the induced current is found to be anti-clockwise by using right-hand thumb rule.
6. The leftward motion of arm AB decreases magnetic flux. The induced current, this time produce a magnetic field inward direction. Flux decrease is opposed by flow of induced current, it flows in a clockwise direction.
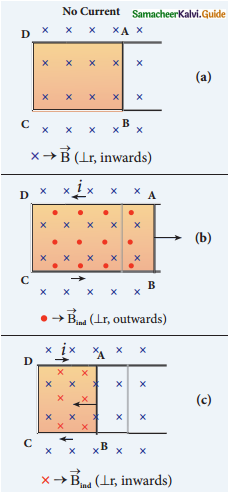
Question 2.
Explain the simple demonstration of the production of eddy current.
Answer:
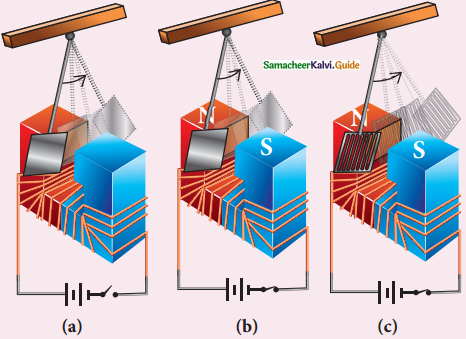
1. Consider a pendulum oscillate between poles of a powerful electromagnet.
2. the First electromagnet is switched off, the pendulum is slightly displaced and released. It begins to oscillate and execute a large number of oscillations before stopping Friction is only damping force.
3. When the electromagnet is switched on, the disc of the pendulum is made to oscillate, eddy currents are produced in it which oppose the oscillation.
4. A heavy damping force of eddy currents will bring the pendulum to rest within few oscillations.
5. If some slots are cut in the disc, eddy currents are reduced. The pendulum now execute several oscillations before coming to rest.
6. This clearly demonstrates the production of eddy current in the disc of the pendulum.
Question 3.
Derive the equation for mutual inductance between two long co-axial solenoids.
Answer:
Consider two long co-axial solenoids of the same length l, A1 and A2 be an area of two solenoids n1 and n2 be the turn density i1 is current in solenoid 1.
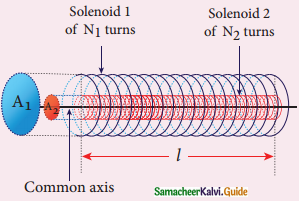
B1 = µ0 n1 i1
Magnetic flux Φ21 = \(\int_{A_{2}} \overrightarrow{B_{1}} \cdot \overrightarrow{d A}\) = B1 A2(0 = 0°)
Flux with total turns N2
N2 φ21 = (n2 l) (µ0 n1 i1) A
N2 φ21 = (µ0 n1 n2 A2 l) i1 ………………(1)
N2 φ21 = M21 i1
Comparing (1) and (2)
M21 = µ0 n1 n2 A2 l …………………..(3)
Magnetic field produced by solenoid 2 when carrying current i2
B2 = µ0 n2 i2
Φ12 = ∫(A2) B2 → . dA → = B2 A2
= (µ0 n1 n2) A2
N1 Φ12 = (n1 l) (µ0 n2 i2) A2
N1 Φ12 = (µ0 n1 n2 A2 l) i2
N1 Φ12 = M12 i2
M12 i2 = (µ0 n1 n2 A2 l) i2
M12 = µ0 n1 n2 A2 l ………………..(4)
Mutual inductance between two long co axial solenoid
M = µ0 n1 n2 A2 l ……………(5)
For relative permittivity µ
M = µn1 n2 A2 l
M = µ0 µr n1 n2 A2 l.
![]()
Question 4.
Find the instantaneous current when the AC circuit containing only the capacitor and find the capacitive reactance.
Answer:
1. Consider a circuit containing a capacitor.
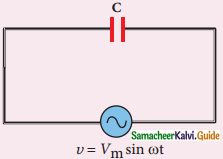
2. The alternating voltage is ν = Vm sin ωt ……………(1)
emf a cross capacitor is q/c
According to Kirchoff’s loop rule
ν = q/C = 0
q = C Vm sin ωt
i = \(\frac{\mathrm{dq}}{\mathrm{dt}}\) = \(\frac{d}{d t}\) (C Vm sin ωt)
= C Vm \(\frac{d}{d t}\) sin ωt
= C Vm ω cos ωt
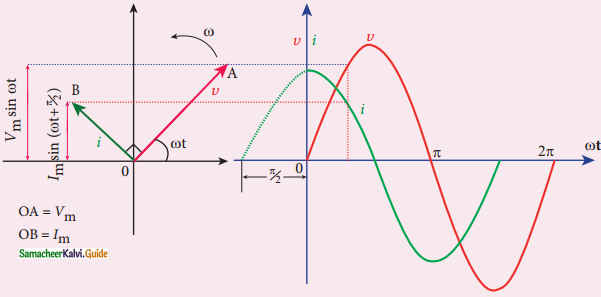
i = \(\frac{\mathrm{V}_{\mathrm{m}}}{\mathrm{I} / \mathrm{C} \omega}\) sin (ωt + π/2)
Instantaneous Current i = I m sin (ωt + π/2)
I m = \(\frac{\mathrm{V}_{\mathrm{m}}}{1 / \omega \mathrm{c}}\) peak value of alternating current.
Current leads the voltage by π/2 (or) 90°
Capacitive Reactance χC:
Resistance offered by capacitor is known as capacitive reactance χC = \(\frac{1}{\mathrm{C} \omega}\)
It varies inversely with frequency,
χC = \(\frac{1}{\mathrm{C} = [latex]\frac{1}{2 \pi \mathrm{fC}}=\frac{1}{0}\) = ∞
Capacitive circuit offers infinite resistance to the steady current.
Question 5.
Explain the effect of series resonance and draw the Resonance curve.
Answer:
1. When Series resonance occurs, the impedance of the circuit is minimum and equal to the resistance of the circuit, current in the circuit becomes maximum.
2. This is shown in the Resonance curve drawn between current and frequency. At resonance impedance is
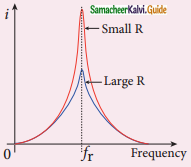
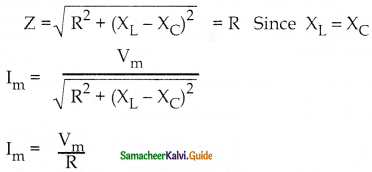
Question 6.
List out the advantages and disadvantages of AC over DC.
Answer:
Advantages:
- Generation of AC is cheaper than DC.
- At high voltage transmission loss is small.
- We can easily convert AC to DC by rectifiers.
Disadvantages:
- We cannot use AC for certain applications like charging of batteries, electroplating, electric traction, etc.
- At high voltage, it is more dangerous to work with AC than DC.
![]()
Question 7.
Explain energy conservation of loop in the magnetic field and prove that mechanical work done in moving loop appears as thermal energy in the loop.
Answer:
1. In order to move loop with constant velocity constant \(\overrightarrow{\mathrm{V}}\) force is equal and opposite to magnetic force applied. Rate of doing work or power is
P = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{V}}\) = F V cos θ, θ = 0° = F V
2. Three deflecting forces \(\overrightarrow{\mathrm{F}}_{1}\), \(\overrightarrow{\mathrm{F}}_{2}\), \(\overrightarrow{\mathrm{F}}_{3}\) acting on three segments of loop, the general equation is
\(\overrightarrow{\mathrm{F}_{\mathrm{d}}}=\overrightarrow{\mathrm{il}} \quad \times \overrightarrow{\mathrm{B}}\)
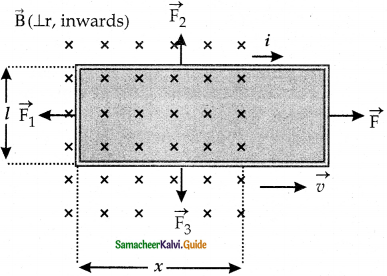
3. \(\overrightarrow{\mathrm{F}}_{1}\), \(\overrightarrow{\mathrm{F}}_{2}\) equal and opposute so cancel each other.

4. When induced current flows in loop Joule heating takes plan Thermal energy is dissipated in the loop.
P = i2 R
P = \(\left(\frac{B l V}{R}\right)^{2}\) R ……………..(2)
(1) = (2)
5. Thus mechanical work done is moving the loop appears as thermal energy in the loop.
![]()
VIII. Additional Problems:
Question 1.
A series LCR circuit with R = 20Ω L = 1.5 H and c = 35 μF is connected to a variable frequency 200 V ac supply when the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
Answer:
R = 20Ω, L = 1.5 H
C = 35 μF = 35 × 10-6 F, V = 200 V
Impedence of the circuit is \(Z=\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
At resonance χL = χC
Z = R = 20Ω
I = \(\frac{V}{Z}=\frac{200}{20}\) = 10A
Average power transferred to the one complete cycle.
P = I2 R
P = 10 × 10 × 20 = 2000W.
Question 2.
An ideal transformer has 460 and 40,000 turns in the primary and secondary coils respectively. Find the voltage developed per turn of the secondary coil if the transformer is connected to a 230 V AC main.
Answer:
Np= 460 turns,
Ns = 40,000 turns
Vp = 230 V

Question 3.
At a hydroelectric power plant, the water pressure head is at a height of 300m and the water flow available is 100 m3s-1. If the turbine generate efficiency is 60% estimate the electric power available from the plant (g = 9.8 ms-2)
Answer:
Height of water pressure head h = 300 m
Volume of water flow per second V = 100 m3 s-1
Efficiency of turbine generator η = 60% = 0.6
Acceleration due to gravity g = 9.8 ms-2
Density of water ρ = 103 kg/m3
Electric Power available from plant = η × hρg
= 0.6 × 300 × 103 × 9.8 × 100
= 176.4 × 106 W
= 176.4 MW
![]()
Question 4.
A long solenoid with 15 turns per cm has small loops of area 2.0 cm2 placed inside the solenoid normal to its axis. If the current carried by the solenoid change steadily from 2.0 A to 4.0 A is 0.1 s. What is the induced emf in the loop while the current is changing?
Answer:
Number of turns in solenoid =15 turns/cm = 1500 turns/m
No. of turns per unit length n = 1500 turns
Small loop Area A = 2.0 cm2 = 2 × 10-4 m2
Change in current di = 4 – 2 = 2 A
Change in time dt = 0.1 s
induced emf in solenoid e = \(\frac{\mathrm{d} \varphi}{\mathrm{d} t}\)
e = \(\frac{d}{d t} (BA)\)
= Aµ0n \(\frac{d i}{d t}\)
= 2 × 10-4 × 4 × 10-7 × 1500 × \(\frac{2}{0.1}\)
= 7.54 × 10-6 V
Induced emf in the loop = 7.54 × 10-6 V.
Question 5.
A transmitter consists of an LC circuit with an inductance of 1 µH and capacitance of 1 µF. What is the wavelength of the electromagnetic waves it emits?
Answer:
Given:
L = 1 µH = 10-6 H
C = 1 µF = 10-6 F