Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 Numbers Ex 1.3 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 1 Numbers Ex 1.3
Question 1.
Verify the closure property for addition and multiplication for the rational numbers \(\frac{-5}{7}\) and \(\frac{8}{9}\).
Answer:
closure property for addition
Let a = \(\frac{-5}{7}\) and b = \(\frac{8}{9}\)
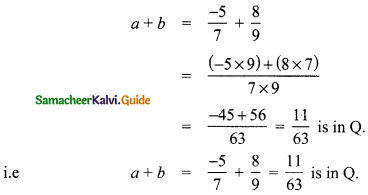
∴ Closure property is true for addition of rational numbers.
Closure property for multiplication
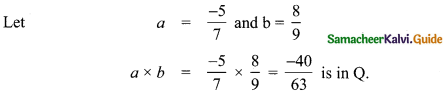
∴ Closure property is true for rnultiplìcation of rational numbers.
![]()
Question 2.
Verify the commutative property for addition and multiplication for the rational numbers \(\frac{-10}{11}\) and \(\frac{-8{33}\).
Answer:
Let a = \(\frac{-10}{11}\) and \(\frac{-8{33}\) be the given rational numbers.
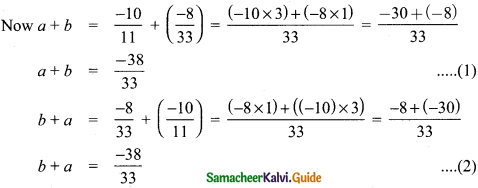
From (1) and (2)
a + b = b + a and hence additionis commutative for rational numbers

From (3) and (4) a × b = b × a
Hence multiplication is commutative for rational numbers.
![]()
Question 3.
Verify the associative property for addition and multiplication for the rational numbers \(\frac{-7}{9}, \frac{5}{6}\) and \(\frac{-4}{3}\).
Answer:
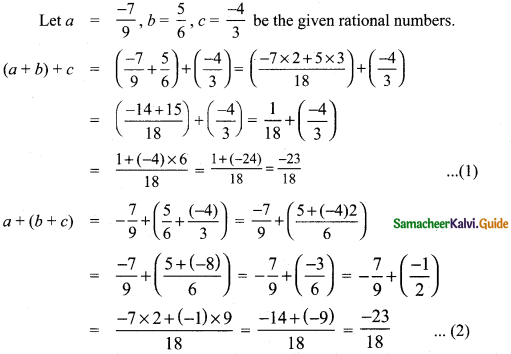
From (1) and (2), (a + b) + c = a + (b + c) is true for rational numbers.
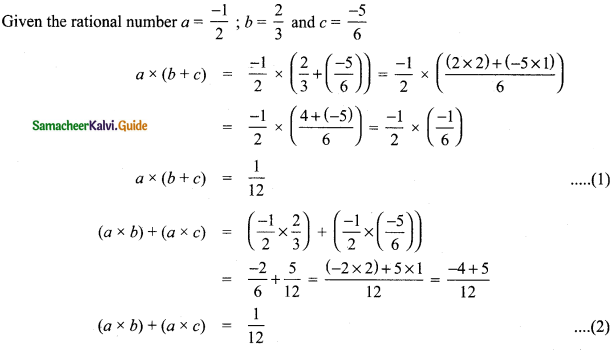
From (1) and (2) (a × b) × c = (a × b) × c is true for rational numbers.
Thus associative property.
![]()
Question 4.
Verify the distributive property a × (b + c) = (a × b) + (a + c) for the rational numbers a = \(\frac{-1}{2}\), b = \(\frac{2}{3}\) and c = \(\frac{-5}{6}\).
Answer:
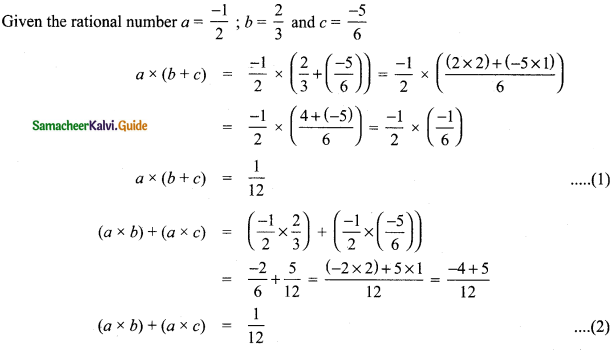
From (1) and (2) we have a × (b + c) = (a × b) + (a × c) is true
Hence multiplication is distributive over addition for rational numbers Q.
![]()
Question 5.
Verify the identity property for addition and multiplication for the rational numbers \(\frac{15}{19}\) and \(\frac{-18}{25}\).
Answer:
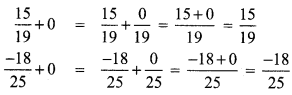
Identify property for addition verified.
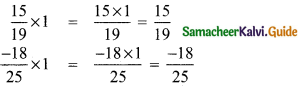
Identify property for multiplication verified.
Question 6.
Verify the additive and multiplicative inverse property for the rational numbers \(\frac{-7}{17}\) and \(\frac{17}{27}\).
Answer:
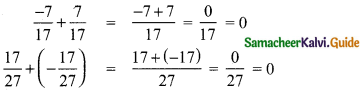
Additive inverse for rational numbers verified.
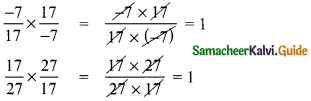
Mulplicative inverse for rational numbers verified.
![]()
Objective Type Questions
Question 7.
Closure property is not true for division of rational numbers because of the number
(A) 1
(B) 1
(C) 0
(D) \(\frac { 1 }{ 2 }\)
Answer:
(C) 0
Question 8.
\(\frac{1}{2}-\left(\frac{3}{4}-\frac{5}{6}\right) \neq\left(\frac{1}{2}-\frac{3}{4}\right)-\frac{5}{6}\) illustrates that subtraction does not satisfy the ________ property for rational numbers.
(A) commutative
(B) closure
(C) distributive
(D) associative
Answer:
(D) associative
![]()
Question 9.
Which of the following illustrates the inverse property for addition?
(A) \(\frac{1}{8}-\frac{1}{8}=0\)
(B) \(\frac{1}{8}+\frac{1}{8}=\frac{1}{4}\)
(C) \(\frac{1}{8}+0=\frac{1}{8}\)
(D) \(\frac{1}{8}-0=\frac{1}{8}\)
Answer:
(A) \(\frac{1}{8}-\frac{1}{8}=0\)
![]()
Question 10.
\(\frac{3}{4} \times\left(\frac{1}{2}-\frac{1}{4}\right)=\frac{3}{4} \times \frac{1}{2}-\frac{3}{4} \times \frac{1}{4}\) illustrates that multiplication is distributive over
(A) addition
(B) subtraction
(C) multiplication
(D) division
Answer:
(B) subtraction