Samacheer Kalvi 8th Maths Guide Chapter 2 Measurements Ex 2.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 2 Measurements Ex 2.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 2 Measurements Ex 2.1

Question 1.
Fill in the blanks:
(i) The ratio between the circumference and diameter of any circle is _______ .
Answer:
π

(ii) A line segment which joins any two points on a circle is a _______ .
Answer:
Chord

(iii) The longest chord of a circle is _______ .
Answer:
Diameter

(iv) The radius of a circle of diameter 24 cm is _______ .
Answer:
12 cm

(v) A part of circumference of a circle is called as _______ .
Answer:
an arc

Question 2.
Match the following

Answer:
(i) – c
(ii) – d
(iii) – e
(iv) – b
(v) – a

Question 3.
Find the central angle of the shaded sectors (each circle is divided into equal sectors).

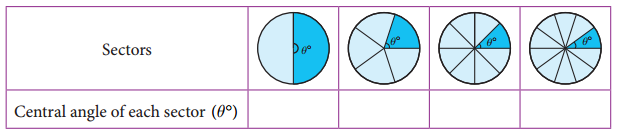
Answer:

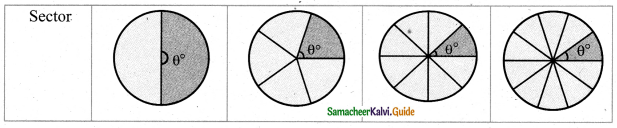
Question 4.
For the sectors with given measures, find the length of the arc, area and perimeter.
(π = 3. 14)
(i) central angle 45° r = 16 cm
Answer:
(i) central angle 45° r = 16 cm
Length of the arc l = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
l = \(\frac{45^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 16 cm
l = \(\frac{1}{8}\) × 2 × 3.14 × 16 cm
l = 12.56 cm
Area of the sector = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr² sq. units
A = \(\frac{45^{\circ}}{360^{\circ}}\) × 3.14 × 16 × 16
A = 100.48 cm²
Perimeter of the sector P = l + 2r units
P = 12.56 + 2(16) cm
p = 44.56 cm

(ii) central angle 120°, d = 12.6 cm
Answer:
∴ r = \(\frac{12.6}{2}\) cm
r = 6.3cm
Length of the arc l = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
l = \(\frac{120^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 63 cm
l = 13.188cm
I = 13.19cm
Area of the sector A = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr² sq. units
A = \(\frac{120^{\circ}}{360^{\circ}}\) × 3 14 × 6.3 × 6.3 cm²
A = 3.14 × 6.3 × 2.1 cm²
A = 41.54 cm²
Perimeter of the sector P = l + 2r cm
P = 13.19 + 2(6.3) cm
= 13.19 + 1.2.6 cm
P = 25.79 cm

Question 5.
From the measures given below, find the area of the sectors.
(i) Length of the arc = 48 m, r = 10 m
Answer:
Area of the sector A = \(\frac{l r}{2}\) sq. units
l = 48m
r = 10m
= \(\frac{48 \times 10}{2}\) m²
= 24 × 10m²
= 240 m²
Area of the sector = 240 m²

(ii) length of the arc = 50 cm, r = 13.5 cm
Answer:
Length of the arc l = 12.5 cm
Radius r = 6 cm
Area of the sector A = \(\frac{l r}{2}\) sq. units
A = \(\frac{12.5 \times 6}{2}\)
A = 12.5 × 3cm²
A = 37.5 cm²
Area of the sector A = 37.5 cm²

Question 6.
Find the central angle of each of the sectors whose measures are given below. (π = \(\frac{22}{7}\))
(i) area = 462 cm², r = 21 cm
Answer:
area = 462 cm², r = 21 cm
Radius of the Sector = 21 cm
Area of the sector = 462 cm²
\(\frac{l r}{2}\) = 462
\(\frac{l \times 21}{2}\) = 462
l = \(\frac{462 \times 2}{21}\)
l = 22 × 2
Length of the arc l = 44 cm

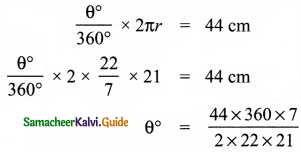
θ° = 120°
∴ Central angle of the sector = 120°

(ii) length of the arc = 44 m, r = 35 m
Answer:
Radius of the sector = 8.4cm
Area of the sector = 18.48 cm²
\(\frac{l r}{2}\) = 18.48
\(\frac{1 \times 8.4}{2}\) = 18.48
l = \(\frac{18.48 \times 2}{8.4}\)
Hint:

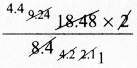
Length of the arc l = 4.4 cm

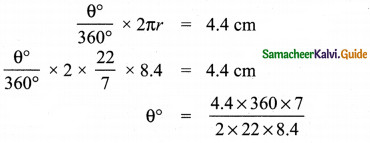
Hint:

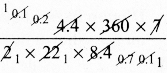
θ° = 30°
Central angle = 30°

Question 7.
A circle of radius 120 m is divided into 8 equal sectors. Find the length of the arc of each of the sectors.
Answer:
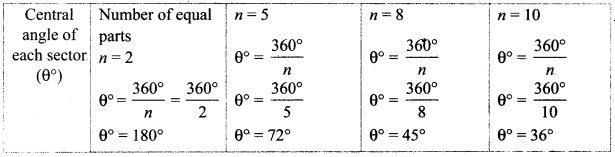
Radius of the circle r = 120 m
Number of equal sectors = 8
∴ Central angle of each sector = \(\frac{360^{\circ}}{n}\)
θ° = \(\frac{360^{\circ}}{8}\)
θ° = 45°
Length of the arc l = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
= \(\frac{45^{\circ}}{360^{\circ}}\) × 2π × 120 m
Length of the arc = 30 × πm

Another method:
l = \(\frac{1}{n}\) × 2πr = \(\frac{1}{8}\) × 2 × π × 120 = 30 π m
Length of the arc = 30 π m

Question 8.
A circle of radius 70 cm is divided into 5 equal sectors. Find the area of each of the sectors.
Answer:
Radius of the sector r = 70 cm
Number of equal sectors = 5
∴ Central angle of each sector = \(\frac{360^{\circ}}{n}\)
θ° = 360°
θ° = 72°
Area of the sector = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr² sq.units
= \(\frac{72^{\circ}}{360^{\circ}}\) × π × 70 × 70cm²
Hint:

= 14 × 70 × πcm²
= 980 πcm²
Note: We can solve this problem using A = \(\frac{1}{n}\) πr² sq. units also.

Question 9.
Dhamu fixes a square tile of 30cm on the floor. The tile has a sector design on it as shown in the figure. Find the area of the sector. (π = 3.14).

Answer:
Side of the square = 30 cm
∴ Radius of the sector design = 30 cm
Given the design of a circular quadrant.
Area of the quadrant = \(\frac{1}{4}\) πr² sq.units
= \(\frac{1}{4}\) × 3.14 × 30 × 30cm²
= 3.14 × 15 × 15cm²
∴ Area of the sector design = 706.5 cm² (approximately)

Question 10.
A circle is formed with 8 equal granite stones as shown in the figure each of radius 56 cm and whose central angle is 45°. Find the area of each of the granite stones. (π = \(\frac { 22 }{ 7 }\))

Answer:
Number of equal sectors ‘n’ = 8
Radius of the sector ‘r’ = 56 cm
Area of each sector = \(\frac{1}{n}\) πr² sq. units
= \(\frac{1}{8} \times \frac{22}{7}\) × 56 × 56cm² =1232 cm²
Area of each sector = 1232 cm² (approximately)