Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.5 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.5
Question 1.
Subtract: -2(xy)2 (y3 + 7x2y + 5) from 5y2 (x2y3 – 2x4y + 10x2)
Answer:
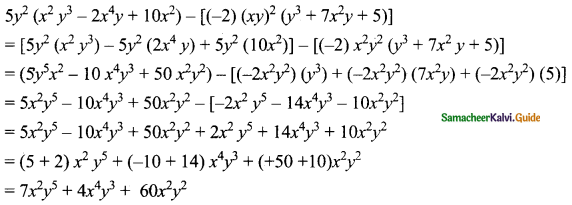
![]()
Question 2.
Multiply (4x2 + 9) and (3x – 2).
Answer:
(4x2 + 9)(3x – 2) = 4x2(3x – 2) + 9(3x – 2)
= (4x2)(3x) – (4x2) (2) + 9(3x) – 9(2)
= (4 × 3 × x × x2) – (4 × 2 × x2) + (9 × 3 × x) – 18
= 12x3 – 8x2 + 27x – 18(4x3 + 9)(3x – 2)
= 12x3 – 8x2 + 27x – 18
Question 3.
Find the simple interest on Rs. 5a2b2 for 4ab years at 7b% per annum.
Answer:
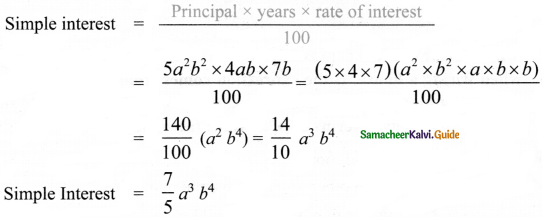
![]()
Question 4.
The cost of a note book is Rs. 10ab. If Babu has Rs. (5a2b + 20ab2 + 40ab). Then how many note books can he buy?
Answer:
For ₹ 10 ab the number of note books can buy = 1.
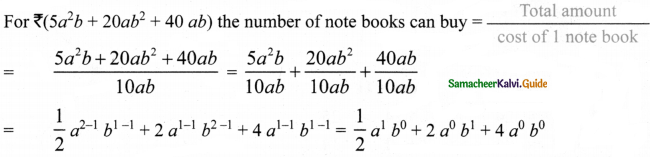
Number of note book he can buy = \(\frac { 1 }{ 2 }\)a + 2b + 4
Question 5.
Factorise: (7y2 – 19y – 6)
Answer:
7y2 – 19y – 6 is of the form ax2 + bx + c where a = 7; b = – 19; c = – 6
| Product = – 42 | Sum = -19 |
| 1 × – 42 = -42 | 1 + (-42) = – 41 |
| 2 × – 21 = – 42 | 2 + (-21) = – 19 |
The product a × c = 7 × – 6 = – 42
sum b = – 19
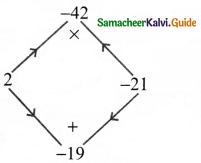
The middle term – 19 y can be written as – 21y + 2y
7y2 – 19y – 6 = 7y2 – 21y + 2y – 6
= 7y(y – 3) + 2(y – 3)
= (y – 3)(7y + 2)
7y2 – 19y – 6 = (y – 3)(7y + 2)
![]()
Question 6.
A contractor uses the expression 4x2 + 11x + 6 to determine the amount of wire to order when wiring a house. If the expression comes from multiplying the number of rooms times the number of outlets and he knows the number of rooms to be (x + 2), find the number of outlets in terms of ’x’. [Hint : factorise 4x2 + 11x + 6]
Answer:
Given Number of rooms = x + 2
Number of rooms × Number of outlets = amount of wire.
(x + 2) × Number of outlets = 4x2 + 11x + 6
Number of outlets = \(\frac{4 x^{2}+11 x+6}{x+2}\) … (1)
Now factorising 4x2 + 11x + 6 which is of the form ax2 + bx + c with a = 4 b = 11 c = 6.
The product a × c = 4 × 6 = 24
sum b = 11
| Product = 24 | Sum = 11 |
| 1 × 24 = 24 | 1 + 24 = 25 |
| 2 × 12 = 24 | 2 + 12 = 14 |
| 3 × 8 = 24 | 3 + 18 = 11 |
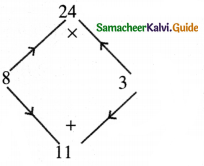
The middle term 11x can be written as 8x + 3x
∴ 4x2 + 11 x + 6 = 4x2 + 8x + 3x + 6
= 4x(x + 2) + 3 (x + 2)
4x2 + 11x + 6 = (x + 2)(4x + 3)
Now from (1) the number of outlets
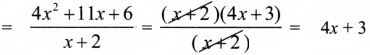
∴ Number of outlets = 4x + 3
![]()
Question 7.
A mason uses the expression x2 + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by (x + 4), what will the width of the room be in terms of x?
Answer:
Given length of the room = x + 4 .
Area of the room = x2 + 6x + 8
Length × breadth = x2 + 6x + 8
breadth = \(\frac{x^{2}+6 x+8}{x+4}\) ….. (1)
Factorizing x2 + 6x + 8, it is in the form of ax2 + bx + c
Where a =1 b = 6 c = 8.
The product a × c = 1 × 8 = 8
sum = b = 6
| Product = 8 | Sum = 6 |
| 1 × 8 = 8 | 1 + 8 = 9 |
| 2 × 4 = 8 | 2 + 4 = 6 |
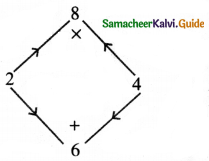
The middle term 6x can be written as 2x + 4x
∴ x2 + 6x + 8 = x2 + 2x + 4x + 8
= x(x + 2) + 4(x + 2)
x2 + 6x + 8 = (x + 2)(x + 4)
Now from (1)
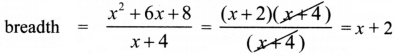
∴ Width of the room = x + 2
![]()
Question 8.
Find the missing term: y2 + (-)x + 56 = (y + 7)(y + -)
Answer:
We have (x + a)(x + b) = x2 + (a + b)x + ab
56 = 7 × 8
∴ y2 + (7 + 8)x + 56 = (y + 7) (y + 8)
Question 9.
Factorise : 16p4 – 1
Answer:
16p4 – 1 = 24p4 – 1 =(22)2 (p2)2 – 12
= (22p2)2 – 12
Comparing with a2 – b2 (a + b)(a – b) where a = 22p2 and b= 1
∴ (22p2)2 – 12 = (22p2 + 1)(22p2 – 1)
= (4p2 + 1)(4p2 – 1)
∴ 16p4 – 1 = (4p2 + 1)(4p2 – 1) = (4p2 + 1)(22p2 – 12)
= (4p2 + 1) [(2p)2 – 12] = (4p2 + 1) (2p + 1)(2p – 1) [∵ using a2 – b2 = (a + b)(a – b)]
∴ 16p4 – 1 = (4p2 + 1)(2p + 1)(2p – 1)
![]()
Question 10.
Factorise : 3x3 – 45x2y + 225xy2 – 375y3
Answer:
= 3x3 – 45x2y + 225xy2 – 375y3
= 3(x3 – 15x2y + 75xy2 – 125y3)
= 3(x3 – 3x2(5y) + 3x(5y)2 – (5y)3)
= 3(x – 5y)3