Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra InText Questions Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra InText Questions
Recap (Text Book Page No. 74 & 75)
Question 1.
Write the number of terms in the following expressions
(i) x + y + z – xyz
Answer:
4 terms
(ii) m2n2c2
Answer:
1 term
![]()
(iii) a2b2c – ab2c2 + a2bc2 + 3abc
Answer:
4 terms
(iv) 8x2 – 4xy + 7xy2
Answer:
3 terms
Question 2.
Identify the numerical co-efficient of each term in the following expressions.
(i) 2x2 – 5xy + 6y2 + 7x – 10y + 9
Answer:
Numerical co efficient in 2x2 is 2
Numerical co efficient in -5xy is -5
Numerical co efficient in 6y2 is 6
Numerical co efficient in 7x is 7
Numerical co efficient in -10y is -10
Numerical co-efficient in 9 is 9
(ii) \(\frac{x}{3}+\frac{2 y}{5}\) – xy + 7
Answer:
Numerical co efficient in \(\frac{x}{3}\) is \(\frac{1}{3}\)
Numerical co efficient in \(\frac{2 y}{5}\) is \(\frac{2}{5}\)
Numerical co efficient in – xy is – 1
Numerical co efficient in 7 is 7
Question 3.
Pick out the like terms from the following:
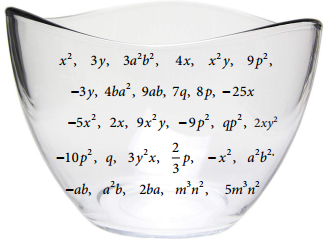
Like Terms
The variables of the terms along with their respective exponents must be same
Examples: x2, 4x2
a2b2, – 5a2b2
2m, – 7m

Answer:
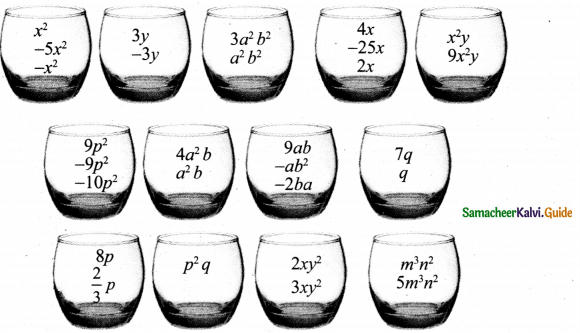
![]()
Question 4.
Add: 2x, 6y, 9x – 2y
Answer:
2x + 6y + 9x – 2y
= 2x + 9x + 6y – 2y
= (2 + 9) x + (6 – 2)y
= 11 x + 4 y
Question 5.
Simplify: (5x3y3 – 3x2y2 + xy + 7) + (2xy + x3y3 – 5 + 2x2y2)
Answer:
(5x3y3 – 3x2y2 + xy + 7) + (2xy + x3y3 – 5 + 2x2y2)
= 5x3y3 + x3y3 – 3x2y2 + 2x2y2 + xy + 2xy + 7 – 5
= (5 + 1)x3y3 + (- 3 + 2)x2y2 + (1 + 2)xy + 2
= 6x3y3 – x2y2 + 3xy + 2
Question 6.
The sides of a triangle are 2x – 5y + 9, 3y + 6x – 7 and -4x + y + 10. Find the perimeter of the triangle.
Answer:
Perimeter of the triangle = Sum of three sides
= (2x – 5y + 9) + (3y + 6x – 7) + (-4x + y + 10)
= 2x – 5y + 9 + 3y + 6x – 7 – 4x + y + 10
= 2x + 6x – 4x – 5y + 3y + y + 9 – 7 + 10
= (2 + 6 – 4)x + (- 5 + 3 + 1)y + (9 – 7 + 10)
= 4x – y + 12
∴ Perimeter of the triangle = 4x – y + 12 units.
![]()
Question 7.
Subtract – 2mn from 6mn.
Answer:
6 mn – (-2mn) = 6mn + (+ 2mn)
= (6 + 2)mn
= 8mn
Question 8.
Subtract 6a2 – 5ab + 3b2 from 4a2 – 3ab + b2.
Answer:
(4a2 – 3ab + b2) – (6a2 – 5ab + 3b2)
= (4a2 – 6a2) + (- 3ab – (-5 ab)] + (b2 – 3b2)
= (4 – 6) a2 + (-3ab + (+ 5ab)] + (1 – 3) b2
= [4+(-6)] a2 + (-3 + 5)ab + [1 + (-3)]b2
= – 2a2 + 2ab – 2b2
Question 9.
The length of a log is 3a + 4b – 2 and a piece (2a – b) is removed from it. What is the length of the remaining log?

Answer:
Length of the log = 3a + 4b – 2
Length of the piece removed = 2a – b
Remaining length of the log = (3a + 4b – 2) – (2a – b)
= (3a – 2a) + [4b – (-b)] – 2
= (3 – 2)a + (4 + 1)b – 2
= a + 5b – 2
![]()
Question 10.
A tin had ‘x’ litre oil. Another tin had (3x2 + 6x – 5) litre of oil. The shopkeeper added (x + 7) litre more to the second tin. Later he sold (x2 + 6) litres of oil from the second tin How much oil was left in the second tin?
Answer:
Quantity of oil in the second tin = 3x2 + 6x – 5 litres.
Quantity of oil added = x + 7 litres
∴ Total quantity of oil in the second tin
= (3x2 + 6x – 5) + (x + 7)litres
= 3x2 + (6x + x) + (-5 + 7) = 3x4 + (6 + 1)x + 2
= 3x2 + 7x + 2litres
Quantity of oil sold = x2 + 6 litres
∴ Quantity of oil left in the second tin
= (3x2 + 7x + 2) – (x2 + 6) = (3x2 – x2) + 7x + (2 – 6)
= (3 – 1)x2 + 7x + (-4) = 2x2 + 7x – 4
Quantity of oil left = 2x2 + 7x – 4 litres
Think (Text Book Page No. 77)
Question 1.
Every algebraic expression is a polynomial. Is this statement true? Why?
Answer:
No, This statement is not true. Because Polynomials contain only whole numbers as the powers of their variables. But an algebraic expression may contains fractions and negative powers on their variables.
Eg. 2y2 + 5y-1 – 3 is a an algebraic expression. But not a polynomial.
![]()
Try These (Text Book Page No. 78)
Find the product of
(i) 3ab2, – 2a2b3
Answer:
(3ab2) × (- 2a2b3) = (+) × (-) × (3 × 2) × (a × a2) × (b2 × b3)
= – 6a3b5
(ii) 4xy, 5y2x, (-x2)
Answer:
(4xy) × (5y2x) × (-x2) = (+) × (+) × (-) × (4 × 5 × 1) × (x × x × x2) × (y × y2)
= -20x4y3
(iii) 2m, – 5n, – 3p
Answer:
(2m) × (-5n) × (-3p) = (+) × (-) × (-) × (2 × 5 × 3) × m × n × p
= + 30 mnp
= 30 mnp
![]()
Think (Text Book Page No. 79)
why 3 + (4x – 7y) ≠ 12 x – 21 y ?
Answer:
Addition and multiplication are different 3 + (4x – 7y) = 3 + 4x – 7y
We can add only like terms.
Try These (Text Book Page No. 79)
Question 1.
MuItipIy
(i) (5x2 + 7x – 3) by -4x2
Answer:
![]()
= – 20x2 – 28x2 + 12x2
(ii) (10x – 7y + 5z) by 6xyz
Answer:
![]()
= 6xyz (10x) + 6xyz (- 7y) + 6xyz (5z)
= (6 × 10)(x × x × y × z) + (6 × – 7) + (x × y × y × z) + (6 × 5)(x × y × z × z)
(iii) (ab + 3bc – 5ca) by 3a2bc
Answer:
(ab + 3bc – 5ca) × (3a2bc ) = ab(3a2bc) + 3bc (3a2bc) – 5ca (3a2bc)
= 3a3b2c + 9a2 b2 c2 – 15a3bc2
(iv) (4m2 – 3m + 7) by – 5m3
Answer:
(4m2 – 3m + 7) × (- 5m3) = 4m2 (- 5m3) – (3m) (- 5m3) + 7(- 5m3)
= – 20m5 + 15m4 – 35m3
![]()
Try These (Text Book Page No. 81)
MuItipIy
(i) (a – 5) and (a + 4)
Answer:
(a – 5)(a + 4) = a(a + 4) – 5(a + 4)
= (a × a) + (a × 4) + (-5 × a) + (-5 × 4)
= a2 + 4a – 5a – 20
= a2 – a – 20
(ii) (a + b) and (a – b)
Answer:
(a + b)(a – b) = a(a – b) + b(a – b)
= (a × a) + (a × -b) + (b × a) + b(-b)
= a2 – ab + ab – b = a2 – b2
(iii) (m4 + n4) and (m – n)
Answer:
(m4 + n4)(m – n) = m4(m – n) + n4(m – n)
(m4 × m) + (m4 × (-n)) + (n4 × m) + (n4 × (-n))
= m5 – m4n + mn4 – n5
![]()
(iv) (2x + 3)(x + 4)
Answer:
(2x + 3)(x + 4) = 2x(x + 4) + 3(x + 4)
= (2x2 × x) + (2x × 4) + (3 × x) + (3 × 4)
= 2x2 + 8x + 3x + 12
= 2x2 + 11x + 12
(v) x – 5)(3x + 7)
Answer:
(x – 5)(3x + 7) = x(3x + 7) – 5(3x + 7)
= (x × 3x) + (x × 7) + (-5 × 3x) + (-5 × 7)
= 3x2 + 7x – 15x – 35
= 3x2 – 8x – 35
(vi) (x – 2)(6x – 3)
Answer:
(x – 2)(6x-3) = x(6x – 3) – 2(6x – 3)
= (x × 6x) + (x × (-3) – (2 × 6x) – (2 × 3)
= 6x2 – 3x – 12x + 6
= 6x2 – 15x + 6
![]()
Think (Text Book Page No. 81)
(i) In 3x2(x4 – 7x3 + 2) what is the highest power in the expression?
Answer:
3x2 (x4 – 7x3 + 2) = (3x2) (x4) + 3x2 (-7x3) + (3x2)2
= 3x6 – 21x5 + 6x2
(ii) Is -5y2 + 2y – 6 = -(5y2 + 2y – 6)? If not, correct the mistake.
Answer:
No, -5y2 + 2y – 6 = -(5y2 + 2y – 6)
Think (Text Book Page No. 83)
Are the following correct?
(i) \(\frac{x^{3}}{x^{8}}\) = x8 – 3 = x5
Answer:
\(\frac{x^{3}}{x^{8}}\) = x8 – 3 = x5 (or) \(\frac{x^{3}}{x^{8}}=\frac{1}{x^{8-3}}=\frac{1}{x^{5}}\)
∴ The given answer is wrong
(ii) \(\frac{10 m^{4}}{10 m^{4}}=0\)
Answer:
\(\frac{10 m^{4}}{10 m^{4}}=\frac{10}{10} m^{4-4}=1\) m0 = 1
[∵ m0 = 1]
∴ The given answer is not correct.
(iii) When a monomial is divided by itself, we will get 1. ?
Answer:
When a monomial is divided by itself we get 1.
\(\frac{x}{x}\) = x1-1 = x0 = 1
∴ The given statement is correct.
![]()
Try These (Text Book Page No. 83)
Divide
(i) 12x3y2 by x2y
Answer:
\(\) = 12x3 – 2y2 – 1 = 12x1y1 = 12xy
(ii) -20a5b2 by 2a3b7
Answer:
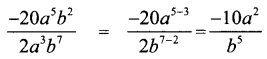
(iii) 28a4c2 by 21ca3
Answer:
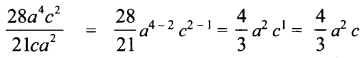
(iv) (3x2y)3 √6x2y3
Answer:
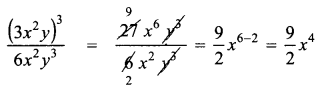
![]()
(v) 64m4 (n2)3 by 4mn
Answer:
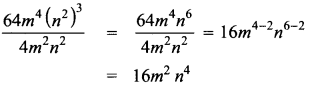
(vi) (8x2y2)3 by (8x2y2)2
Answer:
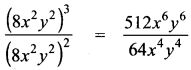
= 8x6 – 4 y6 – 4
= 8x2y2
(vii) 81p2q4 by \(\sqrt{81 p^{2} q^{4}}\)
Answer:
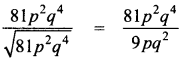
= 9p2 – 1 q4 – 2
= 9pq2
(vii) (4x2y3)0 by \(\frac{\left(x^{3}\right)^{2}}{x^{6}}\)
Answer:
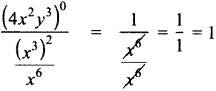
![]()
Think (Text Book Page No. 84)
Are the following divisions correct?
(i) \(\frac{4 y+3}{4}\) = y + 3
Answer:
\(\frac{4 y+3}{4}=\frac{4 y}{4}+\frac{3}{4}=y+\frac{3}{4}\) is the correct answer.
∴ The given statement is not correct
(ii) \(\frac{5 m^{2}+9}{9}\) = 5m2
Answer:
\(\frac{5 m^{2}+9}{9}=\frac{5 m^{2}}{9}+\frac{9}{9}=\frac{5}{9} m^{2}+1\) is the correct answer.
∴ The given statement is not correct
(iii) \(\frac{2 x^{2}+8}{4}\) = 2x2 + 2. If not , correct it.
Answer:
\(\frac{2 x^{2}+8}{4}=\frac{2 x^{2}}{4}+\frac{8}{4}=\frac{1}{2} x^{2}+2\) is the correct answer.
∴ The given statement is not correct
![]()
Try These (Text Book Page No. 84)
(i) (16y5 – 8y2) ÷ 4y
Answer:
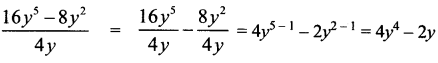
(ii) (p5q2 + 24p3q – 128q3) ÷ 6q
Answer:
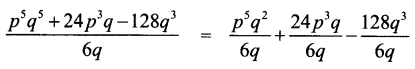
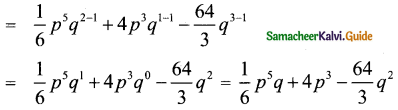
(iii) (4m2n + 9n2m + 3mn) ÷ 4mn
Answer:
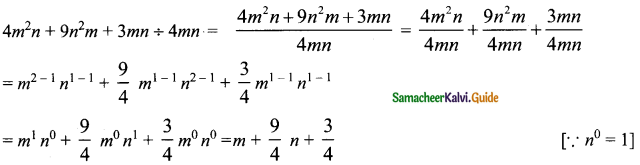
![]()
Try These (Text Book Page No. 86)
Expand the following
Question 1.
(p + 2)2 = ………………….
Answer:
(p + 2)2 = p2 + 2(p)(2) + 22
= p2 + 4p + 4
Question 2.
(3 – a)2 = ………………….
Answer:
(3 – a)2 = 32 – 2(3)(a) + a2
= 9 – 6a + a2
![]()
Question 3.
(62 – x2) = ………………….
Answer:
(62 – x2) = (6 + x)(6 – x)
Question 4.
(a + b)2 – (a – b)2 = ………………….
Answer:
(a + b)2 – (a – b)2 = a2 + 2ab + b2 – (a2 – 2ab + b2)
= a2 + 2ab + b2 – a2 + 2ab – b2
= (1 – 1)a2 + (2 + 2)ab + (+1 – 1)b2 = 4ab
Question 5.
(a + b)2 = (a + b) × ………………….
Answer:
(a + b)2 = (a + b) × (a + b)
Question 6.
(m + n)(…..) = m2 – n2
Answer:
(m + n)(m – n) = m2 – n2
Question 7.
(m + ……)2 = m2 + 14m + 49
Answer:
(m + 7)2 = m2 + 14m + 49
Question 8.
(k2 – 49) = (k + …)(k – …)
Answer:
k2 – 49 = k2 – 72 = (k + 7)(k – 7)
Question 9.
m2 – 6m + 9 = ………………….
Answer:
m2 – 6m + 9 = (m – 3)2
Question 10.
(m – 10)(m + 5) = ………………….
Answer:
(m – 10)(m + 5) = m2 + (-10 + 5)m + (-10)(5) = m2 – 5m – 50
![]()
Think (Text Book Page No. 87)
Which is correct? (3a)2 is equal to
(i) 3a2
(ii) 32a
(iii) 6a2
(iv) 9a2
Answer:
(iv) 9a2
Hint:
(3a)2 = 32 a2 = 9a2
Try These (Text Book Page No. 88)
Expand using appropriate identities.
Question 1.
(3p + 2q)2
Answer:
(3p + 2q)2
Comparing (3p + 2q)2 with (a + b)2, we get a = 3p and b = 2q.
(a + b)2 = a2 + 2ab + b2
(3p + 2q)2 = (3p)2 + 2(3p) (2q) + (2q)2
= 9p2 + 12pq + 4q2
Question 2.
(105)2
Answer:
(105)2 = (100 + 5)2
Comparing (100 + 5)2 with (a + b)2, we get a = 1oo and b = 5.
(a + b)2 = a2 + 2ab + b2
(100 + 5)2 = (100)2 + 2(100)(5) + 52
= 10000 + 1000 + 25
1052 = 11,025
![]()
Question 3.
(2x – 5d)2
Answer:
(2x – 5d)2
Comparing with (a – b)2, we get
a = 2x, b = 5d.
(a – b)2 = a2 – 2ab + b2
(2x – 5d)2 = (2x)2 – 2 (2x) (5d) + (5d)2
= 22x2 – 20 xd + 52d2
= 4x2 – 20xd + 25d2
Question 4.
(98)2
Answer:
(98)2 = (100 – 2)2
Comparing (100 – 2)2 with (a – b)2 we get
a = 100, b = 2
(a – b)2 = a2 – 2ab + b2
(100 – 2)2 = 1002 – 2(100)(2) + 22
= 10000 – 400 + 4
= 9600 + 4
= 9604
![]()
Question 5.
(y – 5) (y + 5)
Answer:
(y – 5) (y + 5)
Comparing (y – 5) (y + 5) with (a – b) (a + b) we get
a = y; b = 5
(a – b) (a + b) = a2 – b2
(y – 5)(y + 5) = y2 – 52
= y2 – 25
Question 6.
(3x)2 – 52
Answer:
(3x)2 – 52
Comparing (3x)2 – 52 with a2 – b2 we have
a = 3x; b = 5
(a2 – b2) = (a + b)(a – b)
(3x)2 – 52 = (3x + 5)(3x – 5)
= 3x(3x – 5) + 5(3x-5)
= (3x) (3x) – (3x) (5) + 5 (3x) – 5 (5)
= 9x2 – 15x + 15x – 25
= 9x2 – 25
Question 7.
(2m + n)(2m + p)
Answer:
(2m + n) (2m + p)
Comparing (2m + n) (2m + p) with (x + a) (x + b) we have
x = 2n; a = n;b = p
(x – a)(x + b) = x2 + (a + b)x + ab
(2m + n) (2m +p) = (2m2) + (n + p)(2m) + (n) (p)
= 22m2 + n(2m) + p(2m) + np
= 4m2 + 2mn + 2mp + np
![]()
Question 8.
203 × 197
Answer:
203 × 197 = (200 + 3)(200 – 3)
Comparing (a + b) (a – b) we have
a = 200, b = 3
(a + b)(a – b) = a2 – b2
(200 + 3)(200 – 3) = 2002 – 32
203 × 197 = 40000 – 9
203 × 197 = 39991
Question 9.
Find the area of the square whose side is (x – 2) units.
Answer:
Side of a square = x – 2
∴ Area = Side × Side
= (x – 2)(x – 2) = x(x – 2) – 2 (x – 2)
= x(x) + (x) (-2) + (-2)(x) + (-2) (-2)
= x2 – 2x – 2x + 4 .
= x2 – 4x + 4 units square
Question 10.
Find the area of the rectangle whose length and breadth are (y + 4) units and (y – 3) units.
Answer:
Length of the rectangle = y + 4
breadth of the rectangle = y – 3
Area of the rectangle = length x breadth
= (y + 4)(y – 3) = y2 + (4 + (-3))y + (4)(-3)
= y2 + y – 12
![]()
Try These (Text Book Page No. 91)
Expand :
(i) (x + 5)3
Answer:
Comparing (x + 5)3 with (a + b)3, we have a = x and b = 4.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 5)3 = x3 + 3x2(5) + 3(x)(5)2 + 53
= x3 + 15x2 + 75x + 125
(ii) (y – 2)3
Answer:
Comparing (y – 2)3 with (a – b)3 we have a = y b = z
(a – b)3 = a3 – 3a2b + 3ab2 – b3
(y – 2)2 = y3 – 3y2(2) + 3y(2)2 + 23
= y3 – 6y2 + 12y + 8
(iii) (x + 1)(x + 4)(x + 6)
Answer:
Comparing (x + 1)(x + 4)(x + 6) with (x + a)(x + b)(x + c) we have
a = 1 b = 4 and c = 6
(x + a)(x + b)(x + c) = x3 + (a + b + c)x2 + (ab + bc + ca)x + abc
= x3 + (1 + 4 + 6)x2 + (1) (4) + (4) (6) + (6) (1)x + (1) (4) (6)
= x3 + 11x2 + (4 + 24 + 6)x + 24
= x3 + 11x3 + 34x + 24
![]()
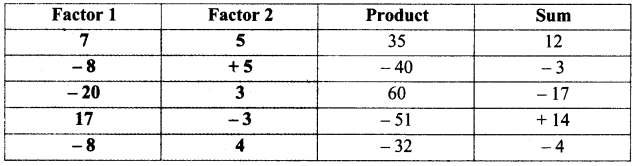
Try These (Text Book Page No. 94)
Find the factors
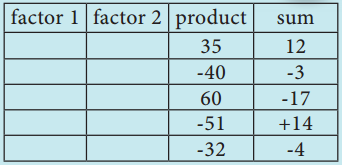
Answer:
Think (Text Book Page No. 94)
x2 – 4(x – 2) = (x2 – 4)(x – 2) Is this correct? If not correct it.
Answer:
(3a)2 = 32a2 = 9a2
x2 – 4 (x – 2) = x2 – 4x + 8
![]()
Try These (Text Book Page No. 95)
Question 1.
3y + 6
Answer:
3y + 6
3y + 6 = 3 × y + 2 × 3
Taking out the common factor 3 from each term we get 3 (y + 2)
∴ 3y + 6 = 3(y + 2)
Question 2.
10x2 + 15y2
Answer:
10x2 + 15y2
10x2 + 15y2 = (2 × 5 × x × x) + (3 × 5 × y × y)
Taking out the common factor 5 we have
10x2 + 15y2 = 5(2x2 + 3y2)
Question 3.
7m(m – 5) + 1(5 – m)
Answer:
7m(m – 5) + 1 (5 – m)
7m(m – 5) + 1(5 – m) = 7m(m – 5) + (-1)(-5 + m)
= 7m(m – 5) – 1 (m – 5)
Taking out the common binomial factor (m – 5) = (m – 5) (7m – 1)
![]()
Question 4.
64 – x2
Answer:
64 – x2
64 – x2 = 82 – x2
This is of the form a2 – b2
Comparing with a2 – b2 we have a = 8, b = x
a2 – b2 = (a + b)(a – b)
64 – x2 = (8 + x)(8 – x)
Question 5.
x2 – 3x + 2
Answer:
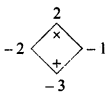
x2 – 3x + 2 = x2 – 2x – x + 2
= x(x – 2) – (x – 2)
= (x – 2)(x – 1)
Question 6.
y2 – 4y – 32
Answer:
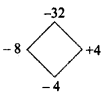
y2 – 4y – 32 = y2 – 8y + 4y – 32
= y(y – 8) + 4(y – 8)
= (y – 8) (y + 4)
![]()
Question 7.
p2 + 2p – 15
Answer:
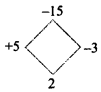
p2 + 2p – 15 = p2 + 5p – 3p – 15
= p(p + 5) -3 (p + 5)
= (p + 5)(p – 3)
Question 8.
m2 + 14m + 48
Answer:
m2 + 14m + 48 = m2 + 8m + 6m +48
= m(m + 8) + 6(m + 8)
= (m + 6)(m + 8)
Question 9.
x2 – x – 90
Answer:
x2 – x – 90 = x2 – 10x + 9x – 90
= x(x – 10) + 9(x – 10)
= (x + 9)(x – 10)
Question 10.
9x2 – 6x – 8
Answer:
9x2 – 6x – 8 = 9x2 – 12x + 6x – 8
= 3x(3x -4) + 2(3x -4)
= (3x + 2)(3x – 4)
![]()
Try These (Text Book Page No. 99)
Identify which among the following are linear equations.
(i) 2 + x = 19
Answer:
Linear as degree of the variable x is 1
(ii) 7x2 – 5 = 3
Answer:
not linear as highest degree of x is 2
(iii) 4p3 = 12
Answer:
not linear as highest degree of p is 3
(iv) 6m + 2
Answer:
Linear, but not an equation
![]()
(v) n = 10
Answer:
Linear equation as degree of n is 1
(vi) 7k – 12 = 0
Answer:
Linear equation as degree of k is 1
(vii) \(\frac{6 x}{8}\) + y = 1
Answer:
Linear equation as degree of x & y is 1
(vii) 5 + y = 3x
Answer:
Linear equation as degree of y & x is 1
(ix) 10p + 2q = 3
Answer:
Linear equation as degree of p & q is 1
(x) x2 – 2x – 4
Answer:
not linear equation as highest degree of x is 2
![]()
Think (Text Book Page No. 99)
(i) Is t(t – 5) = 10 a linear equation? Why?
Answer:
t(t – 5) = 10
= t × t – 5 × t = 10
= t2 – 5t = 10
This is not a linear equations as the highest degree of the variable ‘t’ is 2
(ii) Is x2 = 2x, a linear equation? Why?
Answer:
x2 = 2x
= x2 – 2x = 0
This is not a linear equations as the highest degree of the variable ‘x’ is 2
![]()
Try These (Text Book Page No. 100)
Convert the following statements into linear equations:
Question 1.
On subtracting 8 from the product of 5 and a number, I get 32.
Answer:
Convert to linear equations:
Given that on subtracting 8 from product of 5 and a, we get 32
∴ 5 × x – 8 = 32
∴ 5x – 8 = 32
Question 2.
The sum of three consecutive integers is 78.
Answer:
Sum of 3 consecutive integers is 78
Let integer be bx
∴ x + (x + 1) + (x + 2) = 78
∴ x + x + 1 + x + 2 = 78
∴ 3x + 3 = 78
![]()
Question 3.
Peter had a Two hundred rupee note. After buying 7 copies of a book he was left with 60.
Answer:
Let cost of one book be ‘x’
∴ Given that 200 – 7 × x = 60
∴ 200 – 7x = 60
Question 4.
The base angles of an isosceles triangle are equal and the vertex angle measures 80°.
Answer:
Let base angles each be equal to x & vertex bottom angle is 80°. Applying triangle property, sum of all angles is 180°
∴ x + x + 80 = 180°
∴ 2x + 80 = 180°
Question 5.
In a triangle ABC, ∠A is 100 more than ∠B. Also ∠C is three times ∠A. Express the equation in terms of angle B.
Answer:
Let ∠B = b
Given ∠A = 10° + ∠B = 10 + b
Also given that ∠C = 3 × ∠A = 3 × (10 + b) = 30 + 3b
Sum of the angles = 180°
∠A + ∠B + ∠C = 180°
10 + b + b + 30 + 3b = 180°
∴ 5b + 40 = 180°
![]()
Think (Text Book Page No. 101)
Can you get more than one solution for a linear equation?
Answer:
Yes, we can get. Consider the below line or equation.
x + y = 5
here,when x = 1, y = 4
when x = 2, y = 3
x = 3, y = 2
x = 4, y = 1
Hence, we get multiple solutions for the saine linear equation.
Try These (Text Book Page No. 101)
Identify which among the following are linear equations.
(i) 2 + x = 10
Answer:
2 + x = 10
⇒ x = \(\frac{10}{2}\) = 5
(ii) 3 + x = 5
Answer:
3 + x ⇒ 5
x = 5 – 3 = 2
(iii) x – 6 = 10
Answer:
x – 6 = 10
x = 10 + 6 = 16
(iv) 3x + 5 = 2
Answer:
⇒ 3x + 5 = 2
3x = 2 – 5 = -3
![]()
(v) \(\frac{2 x}{7}\) = 3
Answer:
⇒ 2x = 3 × 7 = 21
x = \(\frac{2 1}{2}\)
(vi) – 2 = 4m – 6
Answer:
⇒ -2x = 4m – 6
– 2 + 6 = 4m
4 = 4m
m = \(\frac{4}{4}\) = 1
(vii) 4(3x – 1) = 80
Answer:
⇒ 4(3x – 1) = 80
12x – 4 = 80
12x = 80 + 4 = 84
x = \(\frac{84}{12}\) = 7
(viii) 3x – 8 = 7 – 2x
Answer:
⇒ 3x – 8 = 7 – 2x
3x + 2x = 7 +8 = 15
5x = 15
x = \(\frac{15}{5}\) = 3
(ix) 7 – y = 3(5 – y)
Answer:
⇒ 7 – y = 3(5 – y)
7 – y = 15 – 3y
3y – y = 15 – 7
2y = 8
y = \(\frac{8}{2}\) = 4
(x) 4(1 – 2y) – 2(3 – y) = 0
Answer:
⇒ 4(1 – 2y) – 2(3 – y) = 0
4 – 8y – ó – 2y = 0
– 2 – 6y = 0
6y = -2
y = \(\frac{-2}{6}=\frac{-1}{3}\)
![]()
Think (Text Book Page No. 102)
Question 1.
“An equation is multiplied or divided by a non zero number on either side:’ Will there be any change in the solution?
Answer:
Not be any change in the solution
Question 2.
“An equation is multiplied or divided by two different numbers on either side. What will happen to the equation?
Answer:
When an equation is multiplied or divided by 2 different numbers on either side, there will be a change in the equation & accordingly, solution will also change.
Think (Text Book Page No. 104)
Suppose we take the second piece to be x and the first piece to be (200 – x), how will the steps vary ? Will the answer be different?
Answer:
Let 2nd piece be ‘x’ & 1st piece is 200 – x
Given that 1st piece is 40 cm smaller than hence the other piece
∴ 200 – x = 2 × x – 40
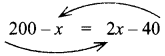
∴ 200 + 40 = 2x + x
240 = 3x
∴ x = \(\frac{240}{3}\) = 80
∴ 1st piece = 200 – x = 200 – 80 = 120 cm
2nd piece = x = 80 cm
The answer will not change
![]()
Think (Text Book Page No. 109)
If instead of (4,3), we write (3,4) and tn to mark it, will it represent ‘M’ again?
Answer:
Let 3, 4 be M. when we mark, we find that it is a different point and not ‘M’
Try These (Text Book Page No. 111)
Question 1.
Complete the table given below.
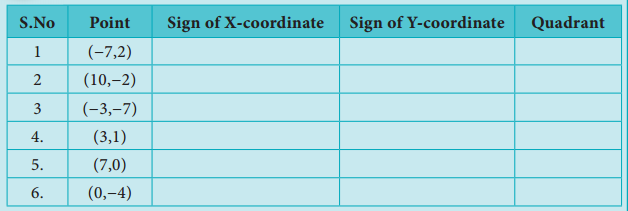
Answer:
![]()
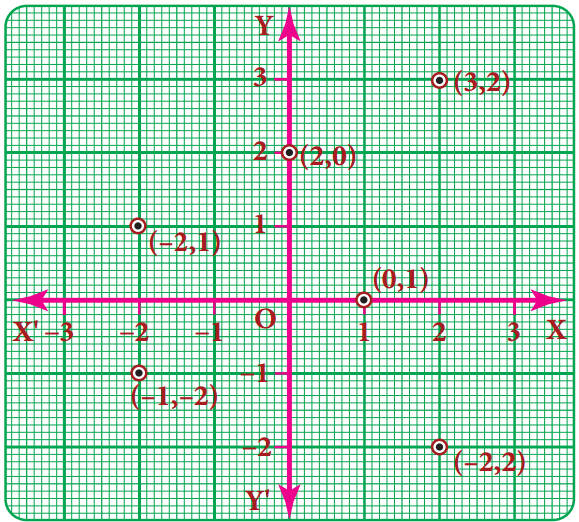
Question 2.
Write the coordinates of the points marked in the following figure
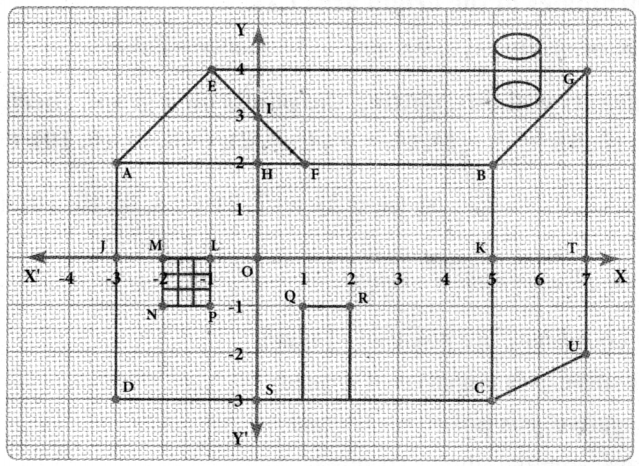
Answer:
A – (-3, 2)
B – (5, 2)
C – (5, -3)
D – (-3, 3)
E – (-1, 4)
F – (1, 2)
G – (7, 4)
H – (0, 2)
I – (0, 3)
J – (-3, 0)
K – (5, 0)
L – (-1, 0)
M – (-2, 0)
N – (-2 ,-1)
O – (0, 0)
P – (-1, -1)
Q – (1, -1)
R – (2, -1)
S – (0, -3)
T – (7, 0)
U – (7, -2)
![]()
Think (Text Book Page No. 114)
Which of the points (5, -10) (0, 5) (5, 20) lie on the straight line x = 5?
Answer:
All points on the line X = 5 will have X-coordinate as 5. Therefore, any point with X – coordinate as 5 will lie on X = 5 line. Hence the points (5, — 10) & (5, 20) will lie on X = 5
Try These (Text Book Page No. 117)
Identify and correct the errors
(i)
Answer:
![]()
(ii)
Answer:
![]()
(iii)
Answer:
