Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics Ex 4.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics Ex 4.4
Question 1.
Fill in the blanks
(i) A can finish a job in 3 days whereas B finishes it in 6 days. The time taken to complete the job working together is __________days.
Answer:
2 days
(ii) If 5 persons can do 5 jobs in 5 days, then 50 persons can do 50 jobs in _________ days.
Answer:
5
![]()
(iii) A can do a work in 24 days. If A and B together can finish the work in 6 days, then B alone can finish the work in ________ days.
Answer:
8
(iv) A alone can do a piece of work in 35 days. If B is 40% more efficient than A, then B will finish the work in ___________days.
Answer:
25
(v) A alone can do a work in 10 days and B alone in 15 days. They undertook the work for ₹ 200000. The amount that A will get is .
Answer:
₹ 1,20,000
Question 2.
210 men working 12 hours a day can finish ajob in 18 days. How many men are required to finish the job in 20 days working 14 hours a day?
Answer:
Let the required number of men be x.
| Hours | Day | Men |
| 12 | 18 | 210 |
| 14 | 20 | x |
More working hours ⇒ less men required.
∴ It is inverse proportion.
∴ Multiplying factor is \(\frac{12}{14}\)
Also more number of days ⇒ less men
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{18}{20}\)
∴ x = \(210 \times \frac{12}{14} \times \frac{18}{20}\)
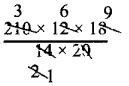
x = 162 men
162 men are required.
![]()
Question 3.
A cement factory makes 7000 cement bags in 12 days with the help of 36 machines. How many bags can be made in 18 days using 24 machines?
Answer:
Let he required number of cement bags be x.
| Days | Machines | Cement bags |
| 12 | 36 | 7000 |
| 18 | 24 | x |
Number of days more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{18}{12}\)
Number of machines more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{24}{36}\)
∴ x = \(7000 \times \frac{18}{12} \times \frac{24}{36}\)
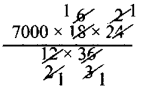
x = 7000 cement bags
7000 cement bags can be made
![]()
Question 4.
A soap factory produces 9600 soaps in 6 days working 15 hours a day. In how many days will it produce 14400 soaps working 3 more hours a day?
Answer:
Let the required number of days be x.
| Soaps | Hours | Days |
| 9600 | 15 | 6 |
| 14400 | (15 + 3) = 18 | x |
To produce more soaps more days required.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{14400}{9600}\)
If more hours spend, less days required.
∴ It is indirect proportion
∴ Multiplying factor = \(\frac{15}{18}\)
∴ x = \(6 \times \frac{14400}{9600} \times \frac{15}{18}\)
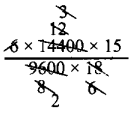
x = \(\frac{15}{2}\)
\(\frac{15}{2}\) days will be needed.
![]()
Question 5.
If 6 container lorries can transport 135 tonnes of goods in 5 days, how many more lorries are required to transport 180 tonnes of goods in 4 days?
Answer:
Let the number of lorries required more = x.
| Container lorries | Goods (tonnes) | Days |
| 6 | 135 | 5 |
| 6 + x | 180 | 4 |
As the goods are more ⇒ More lorries are needed to transport.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{180}{135}\)
Again if more days ⇒ less number of lorries enough.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{5}{4}\)
∴ 6 + x = \(6 \times \frac{180}{135} \times \frac{5}{4}\)
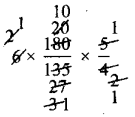
6 + x = 10
x = 10 – 6
x = 4
∴ 4 more lorries are required.
![]()
Question 6.
A can do a piece of work in 12 hours, B and C can do it 3 hours whereas A and C can do it in 6 hours. How long will B alone take to do the same work?
Answer:
Time taken by A to complete the work = 12 hrs.
∴ A’s 1 hr work = \(\frac{1}{12}\) —— (1)
(B + C) complete the work in 3 hrs.
∴ (B + C)’s 1 hour work = \(\frac{1}{3}\) —— (2)
(1) + (2) ⇒
∴ (A + B + C)’s 1 hour work = \(\frac{1}{12}+\frac{1}{3}=\frac{1+4}{12}=\frac{5}{12}\)
Now (A + C) complete the work in 6 hrs.
∴(A + C)’s 1 hour work = \(\frac{1}{6}\)
∴ B’s 1 hour work = (A+ B + C)’s 1 hour work – (A + C)’s 1 hr work
\(=\frac{5}{12}-\frac{1}{6}=\frac{5-2}{12}=\frac{3}{12}=\frac{1}{4}\)
∴ B alone take 4 days to complete the work.
![]()
Question 7.
A and B can do a piece of work in 12 days, while B and C can do it in 15 days whereas A and C can do it in 20 days. How long would each take to do the same work?
Answer:
(A + B) complete the work in 12 days.
∴ (A + B)’s 1 day work = \(\frac{1}{12}\) —— (1)
(B + C) complete the work in 15 days
∴ (B + C)’s 1 day work = \(\frac{1}{15}\) —— (2)
(A + C) complete the work in 20 days
∴ (A + C)’s 1 day work = \(\frac{1}{20}\) —— (3)
Now (1) + (2) + (3) =
[(A + B)+ (B + C) + (A + C)]’s 1 day work = \(\frac{1}{12}+\frac{1}{15}+\frac{1}{20}\)
(2A + 2B + 2C)’s 1 day work = \(\frac{5}{60}+\frac{4}{60}+\frac{3}{60}\)
2(A + B + C)’s 1 day work = \(\frac{5+4+3}{60}\)

LCM = 5 × 4 × 3 = 60
(A + B + C)’s 1 day work = \(\frac{12}{60 \times 2}\)
(A + B + C)’s 1 day work = \(\frac{1}{10}\)
Now A’s I day’s work = (A + B + C)’s 1 day work – (B + C)’s 1 day work
\(=\frac{1}{10}-\frac{1}{15}=\frac{3}{30}-\frac{2}{30}=\frac{1}{30}\)
∴ A takes 30 days to complete the work.
B’s 1 day work – (A + B + C)’s 1 day’s work – (A + C)’s 1 day’s work
\(=\frac{1}{10}-\frac{1}{20}=\frac{6}{60}-\frac{3}{60}\)
\(=\frac{6-3}{60}=\frac{3}{60}=\frac{1}{20}\)
B takes 20 days to complete the work.
C’s 1 day work (A + B + C)’s I day work – (A + B)’s I day work
\(=\frac{1}{10}-\frac{1}{12}=\frac{6}{60}-\frac{5}{60}=\frac{6-5}{60}=\frac{1}{60}\)
∴ C takes 60 days to complete the work.
![]()
Question 8.
Carpenter A takes 15 minutes to fit the parts of a chair while Carpenter B takes 3 minutes more than A to do the same work. Working together, how long will it take for them to fit the parts for 22 chairs?
Answer:
Time taken by A to fit a chair = 15 minutes
Time taken by B = 3 minutes more than A
= 15 + 3 = 118 minutes
∴ As 1 minute work = \(\frac{1}{15}\)
B’s 1 minute work = \(\frac{1}{18}\)
(A+B)’s 1 minutes work = \(\frac{1}{15}+\frac{1}{18}\)
\(\frac{12}{180}+\frac{10}{180}=\frac{22}{180}=\frac{11}{90}\)
∴ Time taken by (A + B) to fit a chair
![]()
LCM = 3 × 5 × 6 = 180
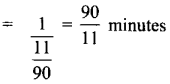
∴ Time taken by (A + B) to fit a chair
= \(\frac{90}{11}\) × 22 = 180 minutes
= \(\frac{180}{60}\) = 3 hours
![]()
Question 9.
A can do a work In 45 days. He works at it for 15 days and then, B alone finishes the remaining work in 24 days. Find the time taken to complete 80% of the work, if they work together.
Answer:
A completes the work in 45 days.
∴ A’s 1 day work = \(\frac{1}{45}\)
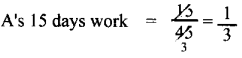
Remaining work = \(1-\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\)
B finishes \(\frac{2}{3}\) rd work in 24 days
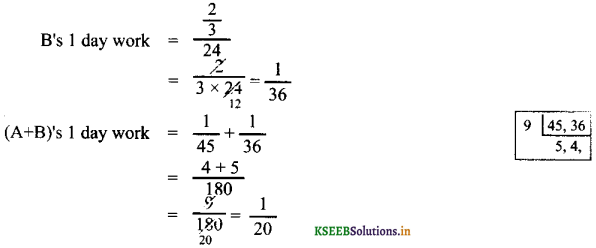
Let x days required
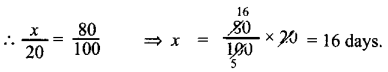
![]()
Question 10.
A is thrice as fast as B. If B can do a piece of work in 24 days then, find the number of days they will take to complete the work together.
Answer:
If B does the work in 3 days, A will do it in I day.
B complete the work in 24 days.
∴ A complete the same work in \(\frac{24}{3}\) = 8 days.
∴ (A + B) complete the work in \(\frac{a b}{a+b}\) days
= \(\frac{24 \times 8}{24+8}\) days
= \(\frac{24 \times 8}{32}\) days = 6 days
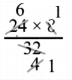
They together complete the work in 6 days.