Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.4
I. Construct the following quadrilaterals with the given measurements and also find their area.
Question 1.
ABCD, AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC = 6.2 cm.
Answer:
Given ABCD, AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC = 6.2 cm.
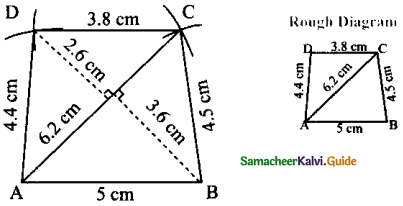
Steps:
- Draw a line segment AB = 5 cm
- With A and B as centers drawn arcs of radii 6.2 cm and 4.5cm respectively and let them cut at C.
- Joined AC and BC.
- With A and C as centrers drawn arcs of radii 4.4cm and 3.8 cm respectively and let them at D.
- Joined AD and CD.
- ABCD is the required quadrilateral.
Calculation of Area:
Area of the quadrilateral ABCD = \(\frac { 1 }{ 2 }\) × d × (h11 + h2) sq. units
= \(\frac { 1 }{ 2 }\) × 6.2 × (2.6 + 3.6)cm2 = 3.1 × 6.2 = 19.22 cm2
![]()
Question 2.
PLAY, PL = 7cm, LA = 6cm, AY = 6cm, PA = 8cm and LY = 7cm.
Answer:
Given PLAY, PL = 7cm, LA = 6cm, AY = 6cm, PA = 8cm and LY = 7cm
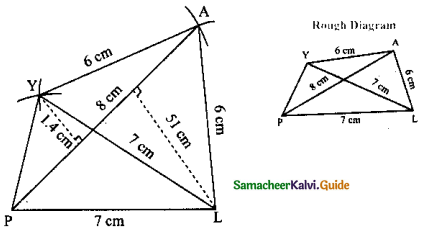
Steps:
- Drawn a line segment PL = 7 cm
- With P and L as centers, drawn arcs of radii 8 cm and 6 cm respectively, let them cut at A.
- Joined PA and LA.
- With L and A as centers, drawn arcs of radii 7 cm and 6 cm respectively and let them cut at Y.
- Joined LY, PY and AY.
- PLAY is the required quadrilateral.
Calculation of Area:
Area of the quadrilateral PLAY = \(\frac { 1 }{ 2 }\) × d × (h1 + h2) sq. units = \(\frac { 1 }{ 2 }\) × 8 × (5.1 + 1.4) cm2
\(\frac { 1 }{ 2 }\) × 8 × 6.5 cm2 = 26 cm2
Area of the quadrilateral = 26 cm2
![]()
Question 3.
PQRS, PQ = QR = 3.5 cm, RS = 5.2 cm, SP = 5.3 cm and ∠Q = 120°.
Answer:
Given PQ = QR = 3.5 cm, RS = 5.2 cm, SP = 5.3 cm and ∠Q = 120°
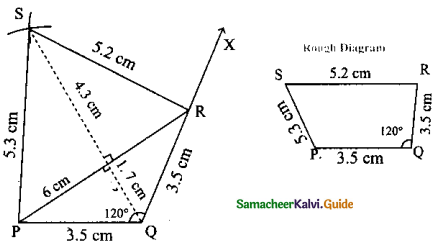
Steps:
- Draw a line segment PQ = 3.5 cm
- Made ∠Q = 120°. Drawn the ray QX.
- With Q as centre drawn an arc of radius 3.5 cm. Let it cut the ray QX at R.
- With R and P as centres drawn arcs of radii 5.2cm and 5.5 cm respectively and let them cut at S.
- Joined PS and RS.
- PQRS is the required quadrilateral.
Calculation of Area:
Area of the quadrilateral PQRS = \(\frac { 1 }{ 2 }\) × d × (h1 + h2) sq. units
= \(\frac { 1 }{ 2 }\) × 6 × (4.3 + 17)cm2
= 3 × 6cm2
= 18 cm2
Area of the quadrilateral PQRS = 18 cm2
![]()
Question 4.
MIND, MI = 3.6 cm, ND = 4 cm, MD = 4 cm, ∠M = 50° and ∠D = 100°.
Answer:
Given MI = 3.6 cm, ND = 4 cm, MD = 4 cm, ∠M = 50° and ∠D = 100°
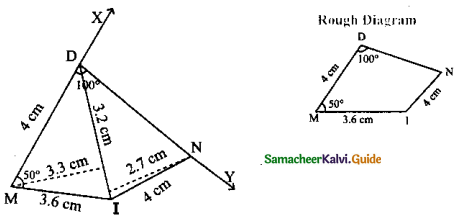
Steps:
- Drawn a line segment MI = 3.6 cm
- At M on MI made an angle ∠IMX = 500
- Drawn an arc with center M and radius 4 cm let it cut MX it D
- At D on DM made an angle ∠MDY = 100°
- With I as center drawn an arc of radius 4 cm, let it cut DY at N.
- Joined DN and IN.
- MIND is the required quadrilateral.
Calculation of Area:
Area of the quadrilateral MIND = \(\frac { 1 }{ 2 }\) × d × (h1 + h2) sq. units = \(\frac { 1 }{ 2 }\) × 3.2 × (2.7 + 33) cm2
= \(\frac { 1 }{ 2 }\) × 3.2 × 6 cm2 = 9.6 cm2
Area of the quadrilateral = 9.6 cm2
![]()
Question 5.
AGRI, AG = 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°.
Answer:
AG = 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°.
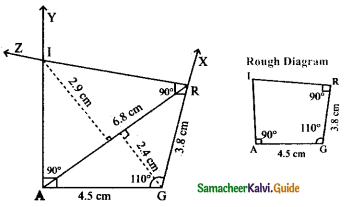
Steps:
- Draw a line segment AG = 4.5 cm
- At G on AG made ∠AGX = 110°
- With G as centre drawn an arc of radius 3.8 cm let it cut GX at R.
- At R on GR made ∠GRZ = 90°
- At A on AG made ∠GAY = 90°
- AY and RZ meet at I.
- AGRI is the required quadrilateral.
Calculation of Area:
Area of the quadrilateral AGRI = \(\frac { 1 }{ 2 }\) × d × (h1 + h2) sq. units = × 6.8 × (2.9 + 2.4) cm2
= \(\frac { 1 }{ 2 }\) × 6.8 × 5.3 × cm2
Area of the quadrilateral = 18.02 cm2
![]()
II. Construct the following trapeziums with the given measures and also find their area.
Question 1.
AIMS with \(\overline{\mathrm{AI}}\) || \(\overline{\mathrm{SM}}\), AI = 6cm, IM = 5cm, AM = 9cm and MS = 6.5cm.
Answer:
Given AI = 6 cm, IM = 5 cm
AM = 9 cm, and \(\overline{\mathrm{AI}}\) || \(\overline{\mathrm{SM}}\)
MS = 6.5 cm
Rough Diagram
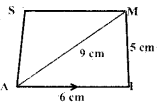
Construction:
Steps:
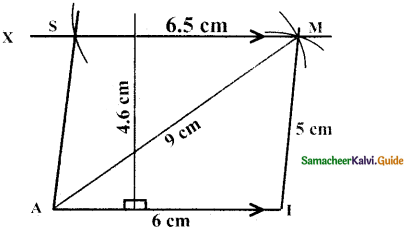
- Draw a line segment AI = 6cm.
- With A and I as centres, draw arcs of radii 9 cm and 5 cm respectively and let them cut at M
- Join AM and IM.
- Draw MX parallel to AI
- With M as centre, draw an arc of radius 6.5 cm cutting MX at S.
- Join AS AIMS is the required trapezium.
Calculation of Area
Area of the trapezium AIMS = \(\frac { 1 }{ 2 }\) × h × (a + b) sq.units
= \(\frac { 1 }{ 2 }\) × 4.6 × (6 + 6.5)
= \(\frac { 1 }{ 2 }\) × 4.6 × 12.5
= 28.75 Sq.cm
![]()
Question 2.
CUTE with \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{ET}}\), CU = 7cm, ∠ UCE = 80° CE = 6cm and TE = 5cm.
Answer:
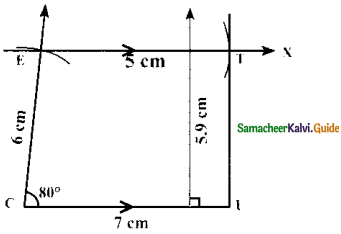
Given: In the trapezium CUTE,
CU = 7cm, ∠UCE = 80°,
CE = 6cm,TE = 5cm and \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{ET}}\)
Rough Diagram
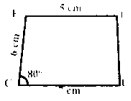
Construction:
Steps:
- Draw a line segment CU = 7cm.
- Construct an angle ∠UCE = 80° at C
- With C as centre, draw an arc of radius 6 cm cutting CY at E
- Draw EX parallel to CU
- With E as centre, draw an arc 7 cm of radius 5 cm cutting EX at T
- Join UT. CUTE is the required trapezium.
Calculation of area:
Area of the trapezium CUTE = \(\frac { 1 }{ 2 }\) × h × (a + b) sq. units
= \(\frac { 1 }{ 2 }\) × 5.9 × (7 + 5)sq. units
= 35.4 sq.cm
![]()
Question 3.
ARMY with \(\overline{\mathrm{AR}}\) || \(\overline{\mathrm{YM}}\), AR = 7cm, RM = 6.5 cm ∠RAY = 100° and ∠ARM = 60°
Answer:
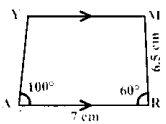
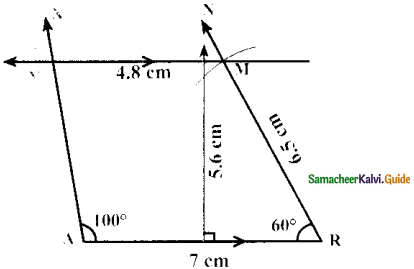
Given: In the trapezium ARMY
AR = 7cm,RM = 6.5cm,
∠RAY = 100° and ARM 60°, \(\overline{\mathrm{AR}}\) || \(\overline{\mathrm{YM}}\)
Rough Diagram
Construction:
Steps:
- Draw a line segment AR = 7 cm.
- Construct an angle ∠RAX = 100° at A
- Construct an angle ∠ARN = 60° at R
- With R as centre, draw an arc of radius 6.5 cm cutting RN at M
- Draw MY parallel to AR
- ARMY is the required trapezium.
Calcualtion of Area:
Area of the trapezium ARMY = \(\frac { 1 }{ 2 }\) × h × (a + b) sq. units
= \(\frac { 1 }{ 2 }\) × 5.6 × (7 + 4.8) sq. units
= \(\frac { 1 }{ 2 }\) × 5.6 × 1.18
= 33.04 sq.cm
![]()
Question 4.
CITY with \(\overline{\mathrm{CI}}\) || \(\overline{\mathrm{YT}}\), CI = 7cm, IT = 5 .5 cm, TY = 4cm and YC = 6cm.
Answer:
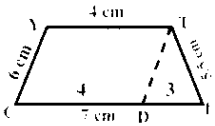
Given: In the trapezium CITY,
CI = 7cm,IT = 5.5cm, TY = 4cm
YC = 6cm, and \(\overline{\mathrm{CI}}\) || \(\overline{\mathrm{YT}}\)
Rough Diagram
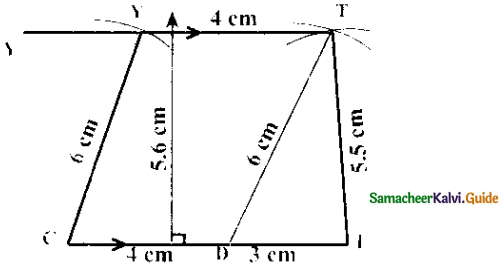
Construction:
Steps:
- Draw a line segment CI = 7 cm.
- Mark a point D on CI such that CD = 4cm
- With D and I as centres, draw arcs of radii 6 cm and 5.5 cm respectively.
Let them cut at T. Join DT and IT. - With C as centre, draw an arc of radius 6 cm.
- Draw TY parallel to Cl. Let the line cut the previous arc at Y.
- Join CY. CITY is the required trapezium.
Construction of area:
Area of the trapezium CITY = \(\frac { 1 }{ 2 }\) × h × (a + b) sq. units
= \(\frac { 1 }{ 2 }\) × 5.5 × (7 + 4)sq.units
= \(\frac { 1 }{ 2 }\) × 5.5 × 11
= 30.25 sq.cm