Samacheer Kalvi 8th Maths Guide Chapter 5 Geometry Ex 5.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.5

I. Construct the following parallelograms with the given measurements and find their area.

Question 1.
ARTS, AR = 6cm, RT = 5cm and ∠ART = 70°.
Answer:
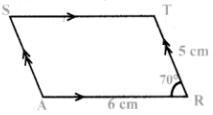
Given : In the Parallelogram ARTS,
AR = 6 cm, RT = 5 cm, and ∠ART = 70°

Rough Diagram

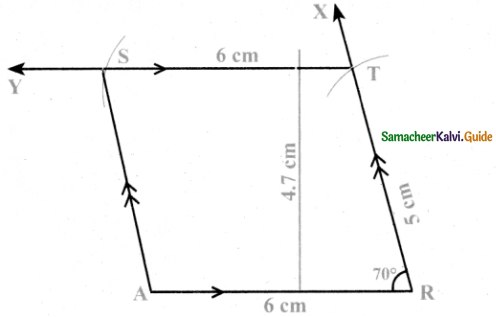
Construction:
Steps:

• Draw a line segment AR = 6 cm.
• Make an angle ∠ART = 70° at R on AR
• With R as centre, draw an arc of radius 5 cm cutting RX at T
• Draw a line TY parallel to AR through T.
• With T as centre, draw an arc of radius 6 cm cutting TY at S. Join AS
• ARTS is the required parallelogram.

Calculation of area:
Area of the parallelogram ARTS = b × h sq. units
= 6 × 4.7 = 28.2 sq.cm

Question 2.
CAMP, CA = 6cm, AP = 8cm and CP = 5.5cm.
Answer:
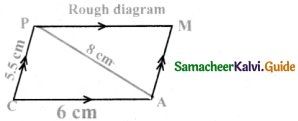
Given : In the parallelogram CAMP,
CA = 6 cm, AP = 8 cm, and CP = 5.5cm

Rough Diagram

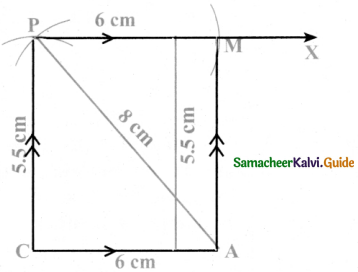
Construction:
Steps:

• Draw a line segment CA = 6 cm.
• With C as centre, draw an arc of length 5.5 cm
• With A as centre, draw an arc of length 8 cm
• Mark the intersecting point of these two arcs as P
• Draw a line PX parallel to CA
• With P as centre draw an arc of radius 6 cm cutting PX at M. Join AM
• CAMP is the required parallelogram.

Calculation of area:
Area of the Parallelogram CAMP = b × h sq. units
= 6 × 5.5 = 33 sq.cm

Question 3.
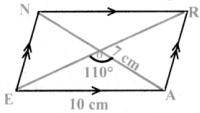
EARN, ER = 10cm, AN = 7cm and ∠EOA = 110° where \(\overline{\mathrm{ER}}\) and \(\overline{\mathrm{AN}}\) intersect at O.
Answer:
Given: In the parallelogram EARN,
ER = 10 cm, AN = 7 cm, and LEOA = 1100
Where \(\overline{\mathrm{ER}}\) and \(\overline{\mathrm{AN}}\) intersect at 0

Rough diagram

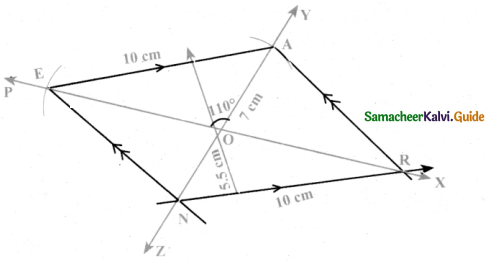
Construction:
Steps:

• Draw a line segment PX. Mark a point O on PX
• Make an angle ∠EOA = 1100 on PX at O
• Draw arcs of radius 3.5 cm with O as centre on either side of PX. Cutting YZ on A and N
• With A as centre, draw an arc of radius 10 cm, cutting PX at E. Join AE
• Draw a line parallel to AE at N cutting PX at R. Join EN and AR
• EARN is the required parallelogram

Calculation of area:
Area of the Parallelogram EARN = b × h sq. units
= 10 × 5.5 = 55 sq.cm

Question 4.
GAIN, GA = 7.5cm, GI = 9cm and ∠GAI = 100°.
Answer:
Given : In the parallelogram GAIN,
GA = 7.5 cm, GI = 9 cm, and ∠GAI = 100°

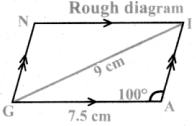
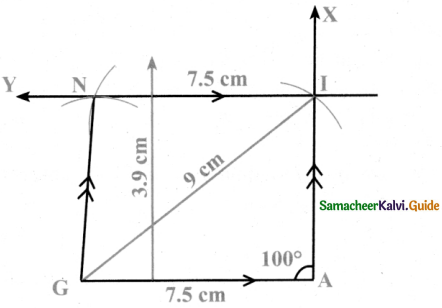
Construction:
Steps:

• Draw a line segment GA = 7.5 cm.
• Make an angle GAI = 100° at A.
• With G as centre, draw an arc of radius 9 cm cutting AX at I. Join GI.
• Draw a line IY parallel to GA through I.
• With I as centre, draw an arc of radius 7.5 cm on IY cutting at N. Join GN
• GAIN is the required parallelogram.

Construction of area:
Area of the Parallelogram GAIN = b × h sq. units
= 7.5 × 39 = 29.25 sq. cm

II. Construct the following rhombuses with the given measurements and also find their area.

(i) FACE, FA = 6 cm and FC = 8 cm
Answer:
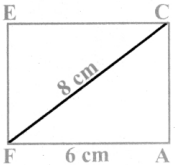
Given FA = 6 cm and FC = 8 cm

Rough Diagram

Steps:

• Drawn a line segment FA = 6 cm.
• With F and A as centres, drawn arcs of radii 8 cm and 6 cm respectively and let them cut at C.
• Joined FC and AC.
• With F and C as centres, drawn arcs of radius 6 cm each and let them cut at E.
• Joined FE and EC.
• FACE is the required rhombus.

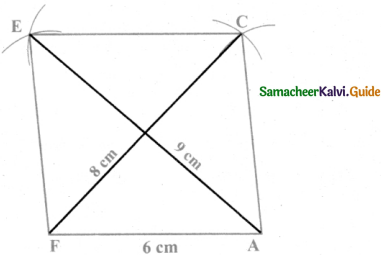
Calculation of Area :
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units = \(\frac { 1 }{ 2 }\) × 8 × 9 sq.units = 36 cm

(ii) CAKE, CA = 5 cm and ∠A = 65°
Answer:
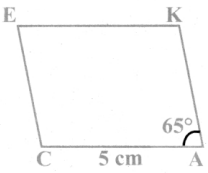
Given CA = 5 cm and ∠A = 65°

Rough Diagram

Steps:

• Drawn a line segment CA = 5 cm.
• At A on AC, made ∠CAX = 65°
• With A as centre, drawn arc of radius 5 cm. Let it cut AX at K.
• With K and C as centres, drawn arcs of radius 5 cm each and let them cut at E.
• Joined KE and CE.
• CAKE is the required rhombus.

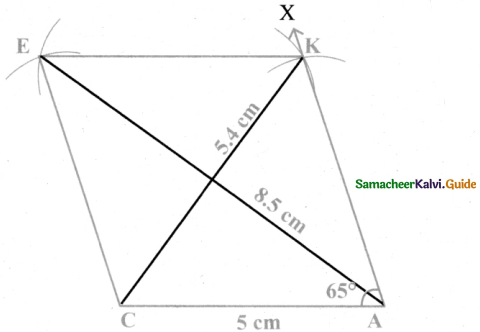
Calculation of Area:
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units
= \(\frac { 1 }{ 2 }\) × 54 × 85cm²
= 22.95 cm²

(iii) LUCK, LC = 7.8 cm and UK = 6 cm
Answer:
Given LC = 7.8 cm and UK = 6 cm

Rough Diagram

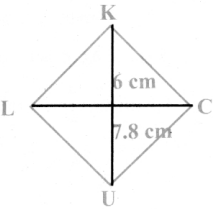
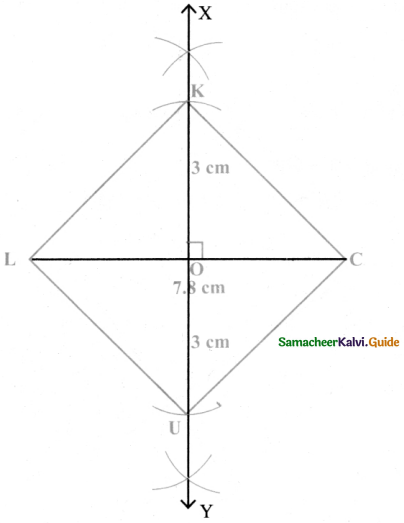
Steps:

• Drawn a line segment LC = 7.8 cm.
• Drawn the perpendicular bisector XY to LC. Let it cut LC at ‘O’
• With O as centres, drawn arc of radius 3 cm on either side of O which cut OX at K and OY at U.
• Joined LU, UC, CK and LK.
• UCK is the required rhombus.

Calculation of Area:
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units
= \(\frac { 1 }{ 2 }\) × 7.8 × 6 cm² = 23.4 cm²

(iv) PARK, PR = 9 cm and ∠P = 70°
Answer:
Given PR = 9 cm and ∠P = 70°

Rough Diagram

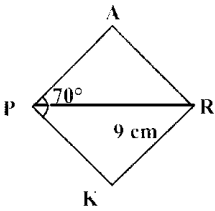
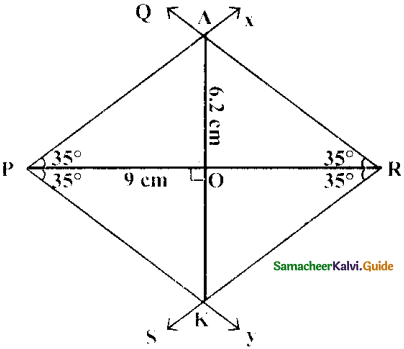
Steps:

• Drawn a line segment PR = 9 cm.
• At P, made ∠RPX ∠RPY = 35° on either side of PR.
• At R, made ∠PRQ = ∠PRS = 35° on either side of PR
• Let PX and RQ cut at A and PY and RS at K.
• PARK is the required rhombus

Constructon of Area:
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units = \(\frac { 1 }{ 2 }\) × 9 × 6.2 cm²
= 27.9 cm²

III. Construct the following rectangles with the given measurements and also find their area.

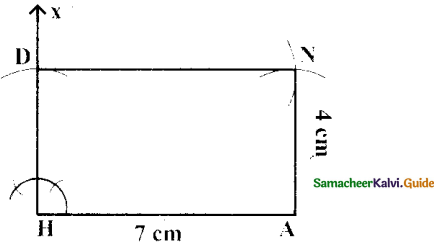
(i) HAND,HA = 7cm and AN = 4 cm
Answer:
Given HA = 7cm and AN = 4 cm

Rough Diagram

Steps:

• Drawn a line segment HA = 7 cm.
• At H, constructed HX ⊥ HA.
• With H as centre, drawn an arc of radius 4 cm and let it cut at HX at D.
• With A and D as centres, drawn arcs of radii 4 cm and 7 cm respectively and let them cut at N.
• Joined AN and DN.
• HAND is the required rectangle.

calculation of’ area :
Area of the rectangle HAND = l × b sq.units
= 7 × 4 cm²
= 28 cm²

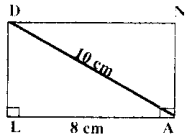
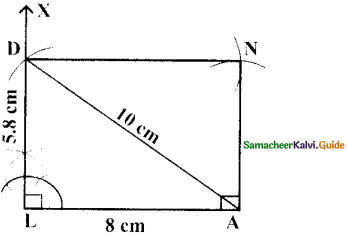
(ii) LAND, LA = 8cm and AD = 10 cm
Answer:
Given LA = 8cm and AD = 10 cm

Sleps :

• Drawn a line segment LA = 8 cm.
• At L, constructed LX ⊥ LA.
• With A as centre, drawn an arc of radius 10 cm and let it cut at LX at D.
• With A as centre and LD as radius drawn an arc. Also with D as centre and LA as radius drawn another arc. Let then cut at N.
• Joined DN and AN.
• LAND is the required rectangle.

Calcualtion of arca :
Area of the rectangle LAND = l × b sq.units
= 8 × 5.8 cm²
= 46.4 cm²

IV. Construct the following squares with the given measurements and also find their area.

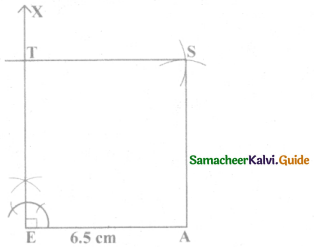
(i) EAST, EA = 6.5 cm
Answer:
Given side = 6.5 cm

Rough diagram

Steps:

• Drawn a line segment EA = 6.5 cm.
• At E, constructed EX⊥ EA.
• With E as centre, drawn an arc of radius 6.5 cm and let it cut EX at T.
• With A and T as centre drawn an arc of radius 6.5 cm each and let them cut at S.
• Joined TS and AS.
• EAST is the required square.

Calcualtion of Area:
Area of the square EAST = a² sq.units
= 6.5 × 6.5 cm²
= 42.25 cm²

(ii) WEST, WS = 7.5 cm
Answer:
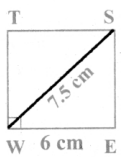
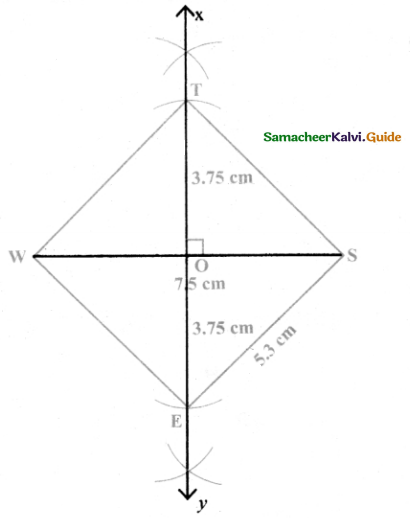
Given diagonal = 7.5 cm

Rough Diagram

Steps:

• Drawn a line segment WS = 7.5 cm.
• Drawn the perpendicular bisector XY to WS. Let it bisect BS at O.
• With O as centre, drawn an arc of radius 3.7 cm on either side of O which cut OX at T and OY at E
• Joined BE, ES, ST and BT.
• WEST is the required square.

Calculation of Area:
Area of the square WEST = a² sq.units
= 5.3 × 53 cm²
= 28.09 cm².