Students can download Maths Chapter 3 Algebra Ex 3.12 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.12
Question 1.
Solve by the method of elimination
(i) 2x – y = 3; 3x + y = 7
Solution:
2x – y = 3 → (1)
3x + y = 7 → (2)
By adding (1) and (2)
5x + 0 = 10
x = \(\frac{10}{5}\)
x = 2
Substitute the value of x = 2 in (1)
2(2) – y = 3
4 – y = 3
-y = 3 – 4
-y = -1
y = 1
The value of x = 2 and y = 1
![]()
(ii) x – y = 5; 3x + 2y = 25
Solution:
x – y = 5 → (1)
3x + 2y = 25 → (2)
(1) × 2 ⇒ 2x – 2y = 10 → (3)
(2) × 1 ⇒ 3x + 2y = 25 → (2)
(3) + (2) ⇒ 5x + 0 = 35
x = \(\frac{35}{5}\)
= 7
Substitute the value of x = 7 in (1)
x – y = 5
7 – y = 5
-y = 5 – 7
-y = -2
y = 2
∴ The value of x = 7 and y = 2
![]()
(iii) \(\frac{x}{10}\) + \(\frac{y}{5}\) = 14; \(\frac{x}{8}\) + \(\frac{y}{6}\) = 15
Solution:
\(\frac{x}{10}\) + \(\frac{y}{5}\) = 14
LCM of 10 and 5 is 10
Multiply by 10
x + 2y = 140 → (1)
\(\frac{x}{8}\) + \(\frac{y}{6}\) = 15
LCM of 8 and 6 is 24
3x + 4y = 360 → (2)
(1) × 2 ⇒ 2x + 4y = 280 → (3)
(2) × 1 ⇒ 3x + 4y = 360 → (2)
(3) – (2) ⇒ -x + 0 = -80
∴ x = 80
Substitute the value of x = 80 in (1)
x + 2y = 140
80 + 2y = 140
2y = 140 – 80
2y = 60
y = \(\frac{60}{2}\)
y = 30
∴ The value of x = 80 and y = 30
![]()
(iv) 3(2x + y) = 7xy; 3(x + 3y) = 11xy
Solution:
3(2x + y) = 7xy
6x + 3y = 7xy
Divided by xy
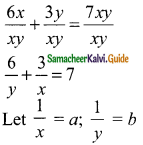
3a + 6b = 7 → (1)
3(x + 3y) = 11xy
3x + 9y = 11xy
Divided by xy
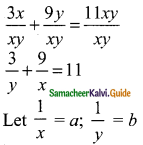
9a + 3b = 11 → (2)
(1) × 3 ⇒ 9a + 18b = 21 → (3)
(2) × 1 ⇒ 9a + 3b = -11 → (2)
(3) – (2) ⇒ 15b = 10
b = \(\frac{10}{15}\) = \(\frac{2}{3}\)
Substitute the value of b = \(\frac{2}{3}\) in (1)
3a + 6 × \(\frac{2}{3}\) = 7
3a + 4 = 7
3a = 7 – 4
3a = 3
a = \(\frac{3}{3}\)
= 1
But \(\frac{1}{x}\) = a
\(\frac{1}{x}\) = 1
x = 1
But \(\frac{1}{y}\) = b
\(\frac{1}{y}\) = \(\frac{2}{3}\)
2y = 3
y = \(\frac{3}{2}\)
∴ The value of x = 1 and y = \(\frac{3}{2}\)
![]()
(v) \(\frac{4}{x}\) + 5y = 7; \(\frac{3}{x}\) + 4y = 5
Solution:
Let \(\frac{1}{x}\) = a
4a + 5y = 7 → (1)
3a + 4y = 5 → (2)
(1) × 4 ⇒ 16a + 20y = 28 →(3)
(2) × 5 ⇒ 15a + 20y = 25 → (4)
(3) – (4) ⇒ a + 0 = 3
a = 3
Substitute the value of a = 3 in (1)
4(3) + 5y = 7
5y = 7 – 12
5y = -5
5y = \(\frac{-5}{5}\) = -1
But \(\frac{1}{x}\) = a
\(\frac{1}{x}\) = 3
3x = 1 ⇒ x = \(\frac{1}{3}\)
The value of x = \(\frac{1}{3}\) and y = -1
![]()
(vi) 13x + 11y = 70; 11x + 13y = 74
Solution:
13x + 11y = 70 → (1)
11x + 13y = 74 → (2)
(1) + (2) ⇒ 24x + 24y = 144
x + y = 6 → (3) (Divided by 24)
(1) – (2) ⇒ 2x – 2y = -4
x – y = -2 → (4) (Divided by 2)
(4) + (3) ⇒ 2x = 4
x = \(\frac{4}{2}\)
= 2
Substitute the value x = 2 in (3)
2 + y = 6
y = 6 – 2
= 4
∴ The value of x = 2 and y = 4
![]()
Question 2.
The monthly income of A and B are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves Rs 5,000 per month, find the monthly income of each.
Solution:
Let the income of “A” be “x” and the income of “B” be “y”.
By the given first condition
x : y = 3 : 4
4x = 3y (Product of the extreme is equal to the product of the means)
4x – 3y = 0 → (1)
Expenditure of A = x – 5000
Expenditure of B = y – 5000
By the given second condition
x – 5000 : y – 5000 = 5 : 7
7(x – 5000) = 5(y – 5000)
7x – 35000 = 5y – 25000
7x – 5y = -25000 + 35000
7x – 5y = 10000 → (2)
(1) × 5 ⇒ 20x – 15y = 0 → (3)
(2) × 3 ⇒ 21x – 15y = 30000 → (4)
(3) – (4) ⇒ x + 0 = 30000
x = 30000
Substitute the value of x in (1)
4 (30000) – 3y = 0
120000 = 3y
y = \(\frac{120000}{3}\) = 40000
∴ Monthly income of A is Rs 30,000
Monthly income of B is Rs 40,000
![]()
Question 3.
Five years ago, a man was seven times as old as his son, while five year hence, the man will be four times as old as his son. Find their present age.
Solution:
Let the age of a man be “x” and the age of a son be “y”
5 years ago
Age of a man = x – 5 years
Age of his son = y – 5 years
By the given first condition
x – 5 = 7(y – 5)
x – 5 = 7y – 35
x – 7y = -35 + 5
x – 7y = -30 → (1)
Five years hence
Age of a man = x + 5 years
Age of his son = y + 5 years
By the given second condition
x + 5 = 4 (y + 5)
x + 5 = 4y + 20
x – 4y = 20 – 5
x – 4y = 15 → (2)
(1) – (2) ⇒ -3y = -45
3y = 45
y = \(\frac{45}{3}\)
= 15
Substitute the value of y = 15 in (1)
x – 7(15) = -30
x – 105 = -30
x = -30 + 105
= 75
Age of the man is 75 years
Age of his son is 15 years
![]()