Students can download Maths Chapter 3 Algebra Ex 3.8 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.8
Question 1.
Factorise each of the following polynomials using synthetic division:
(i) x3 – 3x² – 10x + 24
Solution:
p(x) – x3 – 3x² – 10x + 24
p(1) = 13 – 3(1)² – 10(1) + 24
= 1 – 3 – 10 + 24
= 25 – 13
≠ 0
x – 1 is not a factor
p(-1) = (-1)3 – 3(-1)² – 10(-1) + 24
= – 1 – 3(1) + 10 + 24
= -1 – 3 + 10 + 24
= 34 – 4
= 30
≠ 0
x + 1 is not a factor
p(2) = 23 – 3(2)² – 10(2) + 24
= 8 – 3(4) – 20 + 24
= 8 – 12 – 20 + 24
= 32 – 32
= 0
∴ x – 2 is a factor
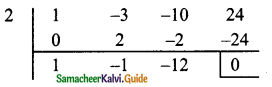
x² – x – 12 = x² – 4x + 3x – 12
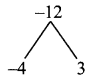
= x(x – 4) + 3 (x – 4)
= (x – 4) (x + 3)
∴ The factors of x3 – 3x² – 10x + 24 = (x – 2) (x – 4) (x + 3)
![]()
(ii) 2x3 – 3x² – 3x + 2
Solution:
p(x) = 2x3 – 3x² – 3x + 2
P(1) = 2(1)3 – 3(1)² – 3(1) + 2
= 2 – 3 – 3 + 2
= 2 – 6
= -4
≠ 0
x – 1 is not a factor
P(-1) = 2(-1)3 – 3(-1)² – 3(-1) + 2
= -2 – 3 + 3 + 2
= 5 – 5
= 0
∴ x + 1 is a factor
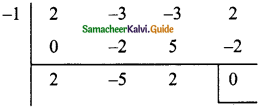
2x² – 5x + 2 = 2x² – 4x – x + 2
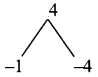
= 2x(x – 2) – 1 (x – 2)
= (x – 2) (2x – 1)
∴ The factors of 2x3 – 3x² – 3x + 2 = (x + 1) (x – 2) (2x – 1)
![]()
(iii) – 7x + 3 + 4x3
Solution:
p(x) = – 7x + 3 + 4x3
= 4x3 – 7x + 3
P(1) = 4(1)3 – 7(1) + 3
4 – 7 + 3
= 7 – 7
= 0
∴ x – 1 is a factor
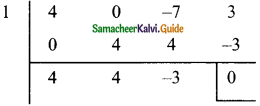
4x² + 4x – 3 = 4x² + 6x – 2x – 3
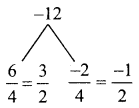
= 2x(2x + 3) – 1 (2x + 3)
= (2x + 3) (2x – 1)
∴ The factors of – 7x + 3 + 4x3 = (x – 1) (2x + 3) (2x – 1)
![]()
(iv) x3 + x² – 14x – 24
Solution:
p(x) = x3 + x² – 14x – 24
p(1) = (1)3 + (1)2 – 14 (1) – 24
= 1 + 1 – 14 – 24
= -36
≠ 0
x + 1 is not a factor.
p(-1) = (-1)3 + (-1)² – 14(-1) – 24
= -1 + 1 + 14 – 24
= 15 – 25
≠ 0
x – 1 is not a factor.
p(2) = (-2)3 + (-2)2 – 14 (-2) – 24
= -8 + 4 + 28 – 24
= 32 – 32
= 0
∴ x + 2 is a factor
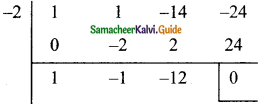
x² – x – 12 = x² – 4x + 3x – 12
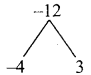
= x(x – 4) + 3 (x – 4)
= (x – 4) (x + 3)
This (x + 2) (x + 3) (x – 4) are the factors.
x3 + x2 – 14x – 24 = (x + 2) (x + 3) (x – 4)
![]()
(v) x3 – 7x + 6
Solution:
p(x) = x3 – 7x + 6
P( 1) = 13 – 7(1) + 6
= 1 – 7 + 6
= 7 – 7
= 0
∴ x – 1 is a factor
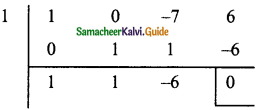
x² + x – 6 = x² + 3x – 2x – 6
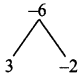
= x(x + 3) – 2 (x + 3)
= (x + 3) (x – 2)
This (x – 1) (x – 2) (x + 3) are factors.
∴ x3 – 7x + 6 = (x – 1) (x – 2) (x + 3)
![]()
(vi) x3 – 10x² – x + 10
p(x) = x3 – 10x2 – x + 10
= 1 – 10 – 1 + 10
= 11 – 11
= 0
∴ x – 1 is a factor
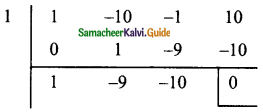
x2 – 9x – 10 = x2 – 10x + x – 10
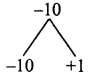
= x(x – 10) + 1 (x – 10)
= (x – 10) (x + 1)
This (x – 1) (x + 1) (x – 10) are the factors.
∴ x3 – 10x2 – x + 10 = (x – 1) (x – 10) (x + 1)
![]()