Students can download Maths Chapter 4 Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Additional Questions
I. Multiple Choice Questions.
Question 1.
The angle sum of a convex polygon with number of sides 7 is ………
(a) 900°
(b) 1080°
(c) 1444°
(d) 720°
Solution:
(a) 900°
Question 2.
What is the name of a regular polygon of six sides?
(a) Square
(b) Equilateral triangle
(c) Regular hexagon
(d) Regular octagon
Solution:
(c) Regular hexagon
![]()
Question 3.
One angle of a parallelogram is a right angle. The name of the quadrilateral is ………
(a) square
(b) rectangle
(c) rhombus
(d) kite
Solution:
(b) rectangle
Question 4.
If all the four sides of a parallelogram are equal and the adjacent angles are of 120° and 60°, then the name of the quadrilateral is ………
(a) rectangle
(b) square
(c) rhombus
(d) kite
Solution:
(c) rhombus
Question 5.
In a parallelogram ∠A : ∠B = 1 : 2. Then ∠A ………
(a) 30°
(b) 60°
(c) 45°
(d) 90°
Solution:
(b) 60°
![]()
Question 6.
Which of the following is a formula to find the sum of interior angles of a quadrilateral of w-sides?
(a) \(\frac{n}{2}\) × 180°
(b) (\(\frac{n+1}{2}\)) 180°
(c) (\(\frac{n-1}{2}\)) 180°
(d) (n – 2) 180°
Solution:
(d) (n – 2) 180°
Question 7.
Diagonal of which of the following quadrilaterals do not bisect it into two congruent triangles?
(a) rhombus
(b) trapezium
(c) square
(d) rectangle
Solution:
(b) trapezium
Question 8.
The point of concurrency of the medians of a triangle is known as ………
(a) circumcentre
(b) incentre
(c) orthocentre
(d) centroid
Solution:
(d) centroid
![]()
Question 9.
Orthocentre of a triangle is the point of concurrency of ………
(a) medians
(b) altitudes
(c) angle bisectors
(d) perpendicular bisectors of side
Solution:
(b) altitudes
Question 10.
ABCD is a parallelogram as shown. Find x and y.
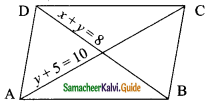
(a) 1, 7
(b) 2, 6
(c) 3, 5
(d) 4, 4
Solution:
(c) 3, 5
Question 11.
A circle divides the plane into part ………
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3
![]()
Question 12.
The longest chord of a circle is a of the circle……….
(a) radius
(b) diameter
(c) chord
(d) secant
Solution:
(b) diameter
Question 13.
Opposite angles of a cyclic quadrilateral are ………
(a) supplementary
(b) complementary
(c) equal
(d) none of these
Solution:
(a) supplementary
Question 14.
The value of x from figure is if ‘O’ is the centre of the circle ………
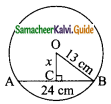
(a) 20 cm
(b) 15 cm
(c) 12 cm
(d) 5 cm
Solution:
(d) 5 cm
![]()
Question 15.
If PQ = x and ‘O’ is the centre of the circle, then x= ………
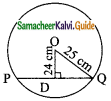
(a) 7 cm
(b) 14 cm
(c) 8 cm
(d) 13 cm
Solution:
(b) 14 cm
Question 16.
In figure OM = ON = 8cm and AB = 30 cm, then CD = ………
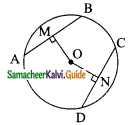
(a) 15 cm
(b) 30 cm
(c) 40 cm
(d) 10 cm
Solution:
(b) 30 cm
Question 17.
O is the centre of a circle, ∠AOB = 100°. Then angle ∠ ACB = ………
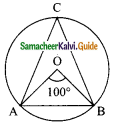
(a) 80°
(b) 40°
(c) 50°
(d) 60°
Solution:
(c) 50°
![]()
Question 18.
In,a circle, with center O, ∠AOB = 20°, ∠BOC = 40°, arc BC = 4 Then length of arc AB will be ………
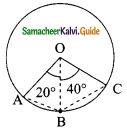
(a) 8 cm
(b) 6 cm
(c) 2 cm
(d) 1 cm
Solution:
(c) 2 cm
Question 19.
In the figure , OC = 3cm and radius of circle is 5 cm. Then AB = ………
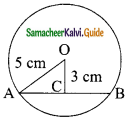
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Solution:
(d) 8 cm
Question 20.
O is the centre of the circle. The value of x in the given diagram is ………
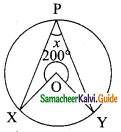
(a) 100°
(b) 160°
(c) 200°
(d) 80°
Solution:
(d) 80°
![]()
II. Answer the following questions.
Question 1.
In the figure find x° and y°.
Solution:
∠ACD = ∠A + ∠B
(An exterior angle of a triangle is sum of its interior opposite angles)
120° = 50° + x°
x° = 120° – 50°
= 70°
In the triangle ABC
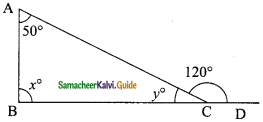
∠A + ∠B + ∠ACB = 180° (Sum of the angles of a Δ)
50° + x + ∠ACB = 180°
50° + 70° + ∠ACB = 180°
∠ACB = 180° – 120°
y = 60°
(OR)
∠ACD + ∠ACB = 180° (Angles of a linear pair)
∠ACB = 180° – 120°
= 60°
The value of x = 70° and y = 60°.
![]()
Question 2.
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.
Sum of all the angles of quadrilateral = 360°.
3x + 5x + 9x + 13x = 360°
30x = 360°
x = \(\frac{360°}{30}\)
= 12°
3x = 3 × 12 = 36°
5x = 5 × 12 = 60°
9x = 9 × 12 = 108°
13x = 13 × 12 = 156°
The required angles of quadrilateral are 36°, 60°, 108° and 156°.
Question 3.
Diagonal AC of a parallelogram ABCD bisects ∠A. Show that
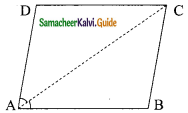
(i) it bisects ∠C also
(ii) ABCD is a rhombus.
Solution:
We have a parallelogram ABCD in which diagonals AC bisect ∠A.
∠DAC = ∠BAC
(i) To prove that AC bisects ∠C
∴ ABCD is a parallelogram
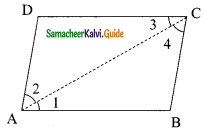
∴ AB || DC and AC is a transversal
∴ ∠1 = ∠3 (Alternate interior angle) …….(1)
Also BC || AD and AC is a transversal
∴ ∠2 = ∠4 (Alternate interior angle) …….(2)
But AC bisects ∠A
∴ ∠1 = ∠2 ……… (3)
From (1), (2) and (3) we get
∠3 = ∠4
∴ AC bisects ∠C.
![]()
(ii) To prove that ABCD is a rhombus.
In ΔABC, we have ∠1 = ∠4 [∴ ∠ 1 = ∠2 = ∠4]
∴ BC = AB (side opposite to equal angles are equal) ……..(4)
Similarly AD = DC …….. (5)
But ABCD is a parallelogram AB = DC (Opposite sides of a parallelogram) ………(6)
From (4), (5) and (6) we have AB = BC = CD = DA.
Thus ABCD is a rhombus.
Question 4.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertex A and C on diagonal BD.
Show that
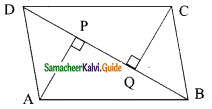
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ.
Solution:
(i) In ΔAPB and ΔCQD we have
∠APB = ∠CQD (90° each)
AB = CD (opposite sides of parallelogram ABCD)
∠ABP = ∠CDQ (AB || CD and AD is a transversal)
Using ASA congruency we have,
ΔAPB ≅ ΔCQD
(ii) Since ΔAPB ≅ ΔCQD
∴ Their corresponding parts are equal.
∴ AP = CQ.
![]()
Question 5.
ABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
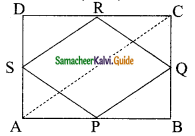
Solution:
In rectangle ABCD, P is the mid-point of AB.
Q is the mid-point of BC. R is the mid-point of CD.
S is the mid-point of DA. AC is the diagonal.
Now in ΔABC,
PQ = \(\frac{1}{2}\) AC and PQ || AC ……. (1)
Similarly in ΔACD,
SR = \(\frac{1}{2}\) AC and SR || AC ……. (2)
From (1) and (2) we get,
PQ = SR and PQ || SR
Similarly by joining BD, we have
PS = QR and PS || QR
i.e. Both pairs of opposite sides of quadrilateral PQRS are equal and parallel.
∴ PQRS is a parallelogram.
![]()
Question 6.
In the figure A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
Solution:
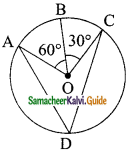
O is the centre of the circle. ∠AOB = 60° and ∠BOC = 30°
Sum of all the angles of quadrilateral = 360°.
∠AOB + ∠BOC = ∠AOC
∴ ∠AOC = 30° + 60°
= 90°
∠ADC = \(\frac{1}{2}\) × 90°
= 45°
Question 7.
In the given figure A, B, C and D are four points on a circle, AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Solution:
In ΔCDE,
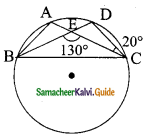
Exterior ∠BEC = Sum of interior opposite angle
130° = ∠EDC + ∠ECD
130° = ∠EDC + 20°
130° – 20° = ∠EDC
110° = ∠EDC
∴ ∠BAC = ∠BDC = 110° (Both the triangles are standing on the same base)
∠BAC = 110°
![]()
Question 8.
In the given figure KLMN is a cyclic quadrilateral. KD is the tangent at K. If ∠N is a diameter ∠NLK = 40° and ∠LNM = 50°. Find ∠MLN and ∠DKL.
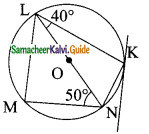
Solution:
LN is a diameter
∠LMN = ∠LKN = 90° (Angle in a semi-circle)
∴ ∠MLN = 90° – 50°
= 40°
∠LNK = 90° – 40°
= 50°
∠DKL = ∠LKN = 50° (angles in the alternate segment)
∴ ∠DKL = 50°
∠MLN = 40° and ∠DKL = 50°
Question 9.
In the given figure ∠PQR = 100°, where P, Q and R are points on a circle with centre ‘O’. Find ∠OPR.
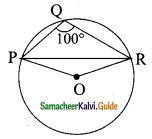
Solution:
∠PQR is the angle subtended by the chord PR in the minor segment.
reflex ∠POR = 2∠PQR
= 2 × 100°
= 200°
Now ∠POR + reflex ∠POR = 360°
∠POR + 200° = 360°
∠POR = 360° – 200°
= 160°
From the given diagram, POR is an isosceles triangle (∴ PO = OR = radii)
∴ ∠OPR = ∠ORP (angles opposite to equal sides)
In ΔOPR,
∠OPR + ∠ORP + ∠POR = 180°
∠OPR + ∠OPR + 160° = 180°
2∠OPR = 180° – 160°
2∠OPR = 20°
∠OPR = \(\frac{20°}{2}\)
= 10°
∴ ∠OPR = 10°
![]()
Question 10.
AB and CD are two parallel chords of a circle which are on either sides of the centre such that AB = 10 cm and CD = 24 cm. Find the radius if the distance between AB and CD is 17 cm.
Solution:
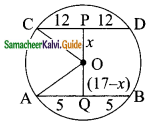
Given AB = 10 cm, CD = 24 cm and PQ = 17 cm.
PC = PD = \(\frac{24}{2}\)
= 12 cm
AQ = QB = \(\frac{10}{2}\)
= 5 cm
Let OP be x; OQ = (17 – x)
In the ΔOPC,
OC² = OP² + PC²
= x² + 12²
In the ΔOAQ,
OA² = AQ² + QO²
= 5² + (17 – x)²
= 25 + 289 + x² – 34x
= 314 + x² – 34x
But OA² = OC²
314 + x² – 34x = x² + 144
-34x = 144 – 314
-34x = -170
34x = 170
x = \(\frac{170}{34}\)
= \(\frac{10}{2}\)
= 5
We know,
OC² = x²+ 144
= 5² + 144
= 25 + 144
OC² = 169
But OC = \(\sqrt{169}\)
= 13
Radius of the circle = 13 cm
= x² + 144
![]()