Samacheer Kalvi 9th Maths Guide Chapter 6 Trigonometry Ex 6.1

Students can download Maths Chapter 6 Trigonometry Ex 6.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.1

Question 1.
From the given figure, find all the trigonometric ratios of angle B.

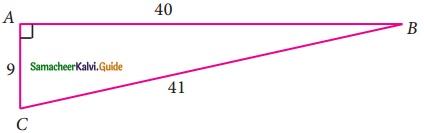
Solution:

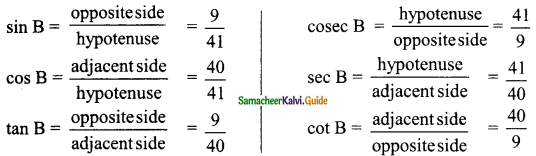
Question 2.
From the given figure, find the values of

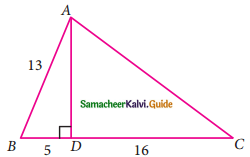
(i) sin B
(ii) sec B
(iii) cot B
(v) tan C
(vi) cosec C
Solution:
In the right ΔABD,
AD² = AB² – BD²
= 13² – 5²
= 169 – 25
= 144
AD = \(\sqrt{144}\)
= 12
In the right ΔADC,
AC² = AD² + DC²
= 12² + 16²
= 144 + 256
= 400
AC = \(\sqrt{400}\)
= 20

Question 3.
If 2 cos θ = √3, then find all the trigonometric ratios of angle θ.
Solution:

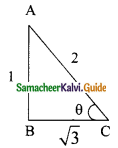
2 cos θ = √3 ⇒ cos θ = \(\frac{√3}{2}\)
AB² = AC² – BC²
= 2² – (√3)² ⇒ = 4 – 3 = 1
AB = √1 = 1

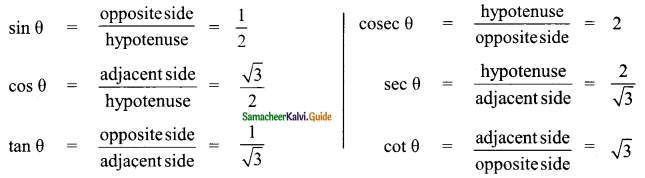
Question 4.
If cos A =\(\frac{3}{5}\), then find the value of \(\frac{sin A-cos A}{2 tan A}\)
Solution:

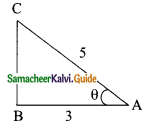
cos A = \(\frac{3}{5}\)
ΔABC
BC² = AC² – AB²
= 5² – 3²
= 25 – 9
= 16
BC = \(\sqrt{16}\) = 4
sin A = \(\frac{4}{5}\); tan A = \(\frac{4}{3}\)

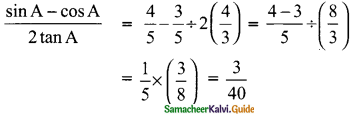
∴ The value of \(\frac{sin A-cos A}{2 tan A}\) = \(\frac{3}{40}\)

Question 5.
If cos A = \(\frac{2x}{1+x_{2}}\) then find the values of sin A and tan A in terms of x.
Solution:
cos A = \(\frac{2x}{1+x_{2}}\)
In the triangle ABC

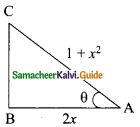
BC² = AC² – AB²
= (1 + x²)² – (2x)²
= 1 + x⁴ + 2x² – 4x²
= x⁴ – 2x² + 1
= (x² – 1)² (or) (1 – x²)² (using (a – b)²)
BC = \(\sqrt{(x^{2}-1)^{2}}\) (or) \(\sqrt{(1-x^{2})^{2}}\)
BC = x² – 1
The value of sin A = \(\frac{BC}{AC}\) = \(\frac{x²-1}{x²+1}\)
tan A = \(\frac{BC}{AB}\) = \(\frac{x²-1}{2x}\)
and
BC = 1 – x²
The value of sin A = \(\frac{1-x²}{1+x²}\)
tan A = \(\frac{1-x²}{2x}\)

Question 6.
If sin θ = \(\frac{a}{\sqrt{a²+b²}}\) then show that b sin θ = a cos θ.
Solution:

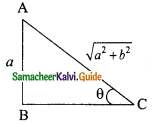
sin θ = \(\frac{a}{\sqrt{a²+b²}}\)
In the triangle ΔABC
BC² = AC² – AB²

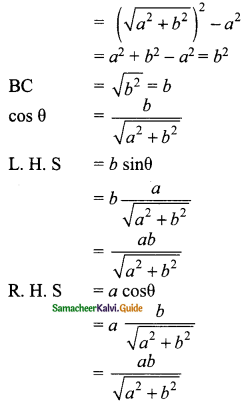
L. H. S = R. H. S

Question 7.
If 3 cot A = 2, then find the value of \(\frac{4sin A-3cos A}{2 sin A+3 Cos A}\)
Solution:

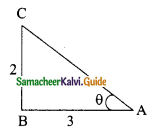
3 cot A = 2 ⇒ cot A = \(\frac{2}{3}\)
AC² = AB² + BC²
= 3² + 2²
= 9 + 4
AC = \(\sqrt{13}\)
cos A = \(\frac{AB}{AC}\) = \(\frac{3}{\sqrt{13}}\)
sin A = \(\frac{BC}{AC}\) = \(\frac{2}{\sqrt{13}}\)
The value of \(\frac{4sin A-3cos A}{2 sin A+3 Cos A}\)

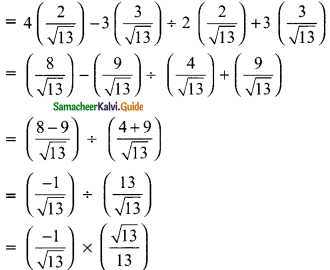
The value is (\(\frac{-1}{13}\))

Question 8.
If cos θ : sin θ = 1 : 2, then find the value of \(\frac{8cos θ-2cos θ}{4 cos θ+2 sin θ}\)
Solution:
cos θ : sin θ = 1 : 2

Aliter:
cos θ : sin θ = 1 : 2
2 cos θ = sin θ ⇒ 2 = \(\frac{sin θ}{cos θ}\) ⇒ 2 = tan θ

∴ The value is \(\frac{1}{2}\)

Question 9.
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅.

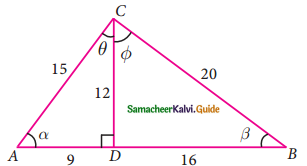
Solution:
In the ΔABC,
AB = 9 + 16 = 25
AC = 15; BC = 20
AB² = 25²
= 625 ……. (1)
AC² + BC² = 15² + 20²
= 225 + 400
= 625 …….. (2)
From (1) and (2) we get
AB² = AC² + BC²
ABC is a right angle triangle at C (Pythagoras theorem)
∴ ∠C = 90°
θ + ∅ = 90°
Also ADC is a right angle triangle ∠ADC = 90° (Given)
BDC is also a right angle triangle ∠BDC = 90° (since ADB is a straight line sum of the two angle is 180°)
From the given diagram

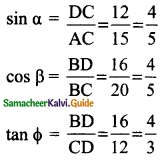
Question 10.
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios).

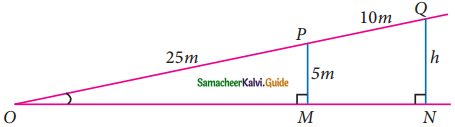
Solution:
Let the angle O be “θ”
In ΔONQ

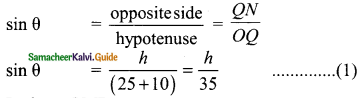
In ΔOMP
sin θ = \(\frac{PM}{OP}\) ⇒ sin θ = \(\frac{5}{25}\)
sin θ = \(\frac{1}{5}\) ……… (2)
From (1) and (2) we get
\(\frac{h}{35}\) = \(\frac{1}{5}\)
5 h = 35 ⇒ h = \(\frac{35}{5}\) = 7
The height of the kite from the ground is 7m.