Students can Download Tamil Nadu 11th Maths Model Question Paper 2 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
TN State Board 11th Maths Model Question Paper 2 English Medium
General Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer - Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
- Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
- Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.
Time: 2:30 Hours
Maximum Marks: 90
PART – 1
I. Choose the correct answer. Answer all the questions: [20 × 1 = 20]
Question 1.
Let R be the set of all real numbers. Consider the following subsets of the plane R × R:
S= {(x, y) : y = x + 1 and 0 < x < 2} and T = {(x, y): x – y is an integer}
Then which of the following is true?
(a) T is an equivalence relation but S is not an equivalence relation.
(b) Neither S nor T is an equivalence relation
(c) Both S and T are equivalence relation
(d) S is an equivalence relation but T is not an equivalence relation.
Answer:
(a) T is an equivalence relation but S is not an equivalence relation.
![]()
Question 2.
If the set A has m elements the set B has n elements and the number of elements in A × B is …………………
(a) m + n
(b) mn
(c) \(\frac{m}{n}\)
(d) m2
Answer:
(b) mn
Question 3.
If \(\frac{ax}{(x+2)(2x-3)}\) = \(\frac{2}{x+2}\) + \(\frac{3}{2x-3}\) then a = ……………….
(a) 8
(b) 7
(c) 5
(d) 4
Answer:
(b) 7
![]()
Question 4.
The number of solutions of x2 + |x – 1| = 1 is ………………….
(a) 1
(b) 0
(c) 2
(d) 3
Answer:
(c) 2
Question 5.
If a, 8, b are in A.P. a, 4, b are in G.P. and a, x, b are in H.P then x = ………………..
(a) 2
(b) 1
(c) 4
(d) 16
Answer:
(a) 2
![]()
Question 6.
If 10 lines are drawn in a plane such that no two of them are parallel and no three are concurrent, then the total number of points of intersection are ……………….
(a) 45
(b) 40
(c) 10!
(d) 210
Answer:
(a) 45
Question 7.
The value of e2logx = …………………..
(a) 2x
(b) x2
(c) \(\sqrt{x}\)
(d) \(\frac{x}{2}\)
Answer:
(b) x2
![]()
Question 8.
The nth term of the sequence 1, 2, 4, 7, 11 …. is …………………
(a) n3 + 3n2 + 2n
(b) n3 – 3n2 + 3n
(c) n\(\frac{(n+1)(n+2)}{3}\)
(d) \(\frac { n^{ 2 }-n+2 }{ 2 } \)
Answer:
(d) \(\frac { n^{ 2 }-n+2 }{ 2 } \)
Question 9.
The last term in the expansion (2+\(\sqrt{3}\))8 is ………………
(a) 81
(b) 27
(c) 9
(d) 3
Answer:
(a) 81
![]()
Question 10.
A line perpendicular to the line 5x -y = 0 forms a triangle with the coordinate axes. If the area of the triangle is 5sq.units, then its equation is …………………..
(a) x + 5y ± 5\(\sqrt{2}\) = 0
(b) x – 5y ± 5\(\sqrt{2}\) = 0
(c) 5x + y ± 5\(\sqrt{2}\) = 0
(d) 5x – y ± 5\(\sqrt{2}\) = 0
Answer:
(a) x + 5y ± 5\(\sqrt{2}\) = 0
Question 11.
A factor of the determinant \(\left|\begin{array}{ccc}
x & -6 & -1 \\
2 & -3 x & x-3 \\
-3 & 2 x & x+2
\end{array}\right|\) is ……………….
(a) x + 3
(b) 2x – 1
(c) x – 2
(d) x – 3
Answer:
(a) x + 3
![]()
Question 12.
If λ\(\vec { a } \) + 2λ\(\vec { j } \) + 2λ\(\vec { k } \) is a unit vector then the value of λ is ………………
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{9}\)
(d) \(\frac{1}{2}\)
Answer:
(a) \(\frac{1}{3}\)
Question 13.
One of the diagonals of parallelogram ABCD with \(\vec { a } \) and \(\vec { b } \) are adjacent sides is \(\vec { a } \) + \(\vec { b } \). The other diagonal BD is ………………….
(a) \(\vec { a } \) – \(\vec { b } \)
(b) \(\vec { a } \) – \(\vec { b } \)
(c) \(\vec { a } \) + \(\vec { b } \)
(d) \(\frac{\vec{a}+\vec{b}}{2}\)
Answer:
(b) \(\vec { a } \) – \(\vec { b } \)
![]()
Question 14.
If (1, 2, 4) and (2, -3λ, -3) are the initial and terminal points of the vector \(\vec { i } \) + 5\(\vec { j } \) – 7\(\vec { k } \) then the value of λ …………………..
(a) \(\frac{7}{3}\)
(b) –\(\frac{7}{3}\)
(c) \(\frac{5}{3}\)
(d) \(\frac{-5}{3}\)
Answer:
(b) –\(\frac{7}{3}\)
Question 15.
If y = mx + c and f(0) =f'(0) = 1 then f(2) = …………………..
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c) 3
![]()
Question 16.
The derivative of (x + \(\frac{1}{x}\))2 w.r.to. x is ………………..
(a) 2x – \(\frac { 2 }{ x^{ 3 } } \)
(b) 2x + \(\frac { 2 }{ x^{ 3 } } \)
(c) 2(x + \(\frac{1}{x}\))
(d) 0
Answer:
(a) 2x – \(\frac { 2 }{ x^{ 3 } } \)
Question 17.
If f(x) is \(\left\{\begin{array}{cc}
a x^{2}-b, & -1<x<1 \\
\frac{1}{|x|}, & \text { elsewhere }
\end{array}\right.\) is differentiable at x = 1, then …………………
(a) a = \(\frac{1}{2}\), b = \(\frac{-3}{2}\)
(b) a = \(\frac{-1}{2}\), b = \(\frac{3}{2}\)
(c) a = \(\frac{-1}{2}\), b = \(\frac{-3}{2}\)
(d) a = \(\frac{1}{2}\), b = \(\frac{3}{2}\)
Answer:
(c) a = \(\frac{-1}{2}\), b = \(\frac{-3}{2}\)
![]()
Question 18.
∫\(\frac { \sqrt { tanx } }{ sin2x } \) dx is ………………
(a) \(\sqrt{tanx}\) + c
(b) 2\(\sqrt{tanx}\) + c
(c) \(\frac{1}{2}\) \(\sqrt{tanx}\) + c
(d) \(\frac{1}{4}\) \(\sqrt{tanx}\) + c
Answer:
(a) \(\sqrt{tanx}\) + c
Question 19.
An urn contains 5 red and 5 black balls. A balls is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. The probability that the second ball drawn is red will be ………………….
(a) \(\frac{5}{12}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{7}{12}\)
(d) \(\frac{1}{4}\)
Answer:
(b) \(\frac{1}{2}\)
![]()
Question 20.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\), and P(B/A) = \(\frac{2}{3}\) then
P(B) = ………………….
(a) \(\frac{1}{6}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{2}\)
Answer:
(b) \(\frac{1}{3}\)
PART – II
II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]
Question 21.
If n(P(A)) = 1024, n(A∪B) = 15 and n(P(B)) = 32 then find n(A∩B)
Answer:
n(P(A)) = 1024 = 210 ⇒ n(A) = 10
n(A∪B) = 15
n(P(B)) = 32 = 25 ⇒ n(B) = 5
We know n(A∪B) = n(A) + n(B) – n(A∩B)
(i.e) 15 = 10 + 5 – n(A∩B)
⇒ n(A∩B) = 15 – 15 = 0
![]()
Question 22.
Simplify (343)2/3
Answer:
(343)2/3 = (73)2/3 = 73×2/3 = 72 = 49
Question 23.
Show that cos36° cos 72° cos 108° cos 144° = \(\frac{1}{16}\)
Answer:
LHS = cos36° cos(90° – 18°) cos(90° – 18°) cos(90° + 18°) cos(180° – 36°)
= sin2 18° cos2 36°
= (\(\frac { \sqrt { 5-1 } }{ 4 } \))2 (\(\frac { \sqrt { 5+1 } }{ 4 } \))2 = \(\frac{1}{16}\) = RHS
![]()
Question 24.
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour?
Answer:
There are 6 red balls, 5 white balls and 5 blue balls.
We have to select 3 balls of each colour.
∴Number of ways of selection = 6C3 × 5C3 × 5C3
= \(\frac { 6! }{ 3!3! } \) × \(\frac { 5! }{ 3!2! } \) × \(\frac { 5! }{ 3!2! } \)
= 20 × 10 × 10 = 2000
Question 25.
Find |A| if A = \(\left[\begin{array}{ccc}
0 & \sin \alpha & \cos \alpha \\
\sin \alpha & 0 & \sin \beta \\
\cos \alpha & -\sin \beta & 0
\end{array}\right]\)
Answer:
\(\left[\begin{array}{ccc}
0 & \sin \alpha & \cos \alpha \\
\sin \alpha & 0 & \sin \beta \\
\cos \alpha & -\sin \beta & 0
\end{array}\right]\)
= 0M11 – sin αM12 + cos αM13
= 0 – sin α(0 – cos α sin β) + cos α (-sin α sin β – 0) = 0
![]()
Question 26.
For any vector prove that \(\vec { r } \) = [\(\vec { r } \).\(\vec { i } \)) + (\(\vec { r } \).\(\vec { j } \))j + [\(\vec { r } \).\(\vec { k } \)}k
Answer:
Let \(\vec { r } \) = x\(\hat { i } \) + y\(\hat { j } \) + z\(\hat { k } \)

![]()
Question 27.
Calculate \(\lim _{x \rightarrow-2}\) (x3 – 3x + 6) (-x2 + 15)
Answer:

Question 28.
Evaluate y = ex sin x
Answer:

Question 29.
Integrate the following with respect to x
\(\frac{4}{3+4x}\) + (10x + 3)9 – 3 cosec(2x + 3) cot (2x + 3)
Answer:
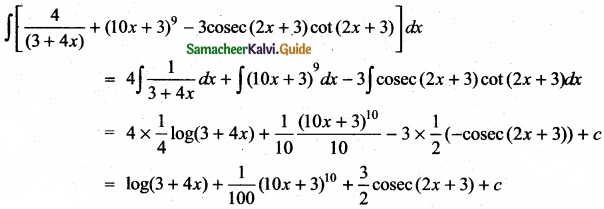
![]()
Question 30.
P(A) = 0.6, P (B) = 0.5 and P(A∩B) = 0.2 find P(A/B)
Answer:
Given that P(A) = 0.6, P(B) = 0.5, and P(A∩B) = 0.2
P(A/B) = \(\frac { p(A∩B) }{ p(B) } \) = \(\frac{0.2}{0.5}\) = \(\frac{2}{5}\)
PART – III
III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]
Question 31.
A quadratic polynomial has one of its zeros 1 + \(\sqrt{5}\) and it satisfies p(1) = 2. Find the quadratic polynomial?
Question 32.
Prove that
- tan-1 (\(\frac{1}{7}\)) + tan-1(\(\frac{1}{13}\)) = tan-1(\(\frac{2}{9}\))
- cos-1\(\frac{4}{5}\) + tan-1\(\frac{3}{5}\) = tan-1\(\frac{27}{11}\)
![]()
Question 33.
The product of three increasing numbers in GP is 5832. If we add 6 to the second number and 9 to the third number, then resulting numbers form an AP. Find the numbers in GP?
Question 34.
Find the equation of the line passing through the point (5, 2) and perpendiular to the line joining the points (2, 3) and (3, -1)?
![]()
Question 35.
Find the area of the triangle whose vertices are (0,0), (1,2) and (4,3)?
Question 36.
If \(\vec { a } \), \(\vec { b } \), \(\vec { c } \) are three vectors such that \(\vec { a } \) + 2\(\vec { b } \) + \(\vec { c } \) = 0 and |\(\vec { a } \)| = 3, |\(\vec { b } \)| = 4, |\(\vec { c } \)| = 7 fimd the angle between \(\vec { a } \) and \(\vec { b } \)
Question 37.
Evaluate: \({ \underset { x\rightarrow 0 }{ lim } }\) \(\frac { 3^{ x }-1 }{ \sqrt { 1+x-1 } } \)
![]()
Question 38.
Find \(\frac{dy}{dx}\) for y = tan-1 \((\frac { cosx+sinx }{ cosx-sinx } )\)
Question 39.
Evaluate: ∫x5 ex2
Question 40.
How many automobile license plates can be made, if each plate contains two different letters followed by three different digits?
PART – IV
IV. Answer all the questions. [7 × 5 = 35]
Question 41.
(a) If f : R – {-1, 1} → R is defined by f(x) = \(\frac { x }{ x^{ 2 }-1 } \), verify whether f is one-to-one or not?
[OR]
(b) Solve: log2 x + log4 x + log8 x = 11
![]()
Question 42.
(a) Prove that \(\frac{\sin x+\sin 3 x+\sin 5 x+\sin 7 x}{\cos x+\cos 3 x+\cos 5 x+\cos 7 x}\) = tan 4x
[OR]
(b) If x + y + z = xyz, then prove that \(\frac { 2x }{ 1-x^{ 2 } } \) + \(\frac { 2y }{ 1-y^{ 2 } } \) + \(\frac { 2z }{ 1-z^{ 2 } } \) = \(\frac { 2x }{ 1-x^{ 2 } } \) \(\frac { 2y }{ 1-y^{ 2 } } \) \(\frac { 2z }{ 1-z^{ 2 } } \)
Question 43.
(a) If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then and the ranks of the words
- GARDEN
- DANGER
[OR]
(b) \(\underset { x\rightarrow a }{ lim } \) \(\frac{\sqrt{x-b}-\sqrt{a-b}}{x^{2}-a^{2}}\) (a>b)
![]()
Question 44.
(a) If the binomial coefficients of three consecutive terms in the expansion of (a + x)n are in the ratio 1 : 7 : 42 then find n?
[OR]
(b) Evalute \(\sqrt { x^{ 2 }+y^{ 2 } } \) = tan-1(\(\frac{y}{x}\))
Question 45.
Let \(\vec { a } \), \(\vec { b } \), \(\vec { c } \) be three vectors such that |\(\vec { a } \)| = 3, |\(\vec { b } \)| = 4, |\(\vec { c } \)| = 5 and each one of them being perpendicular to the sum of the other two, find |\(\vec { a } \) + \(\vec { b } \) + \(\vec { c } \)|.
[OR]
(b) Evaluate ∫sec3 2xdx
![]()
Question 46.
(a) Find all the equations of the straight lines in the family of the lines y = mx – 3, for which m and the x-coordinate of the point of intersection of the lines with x – y = 6 are integers?
[OR]
(b) There are two identical boxes containing respectively 5 white and 3 red balls, 4 white and 6 red balls. A box is chosen at random and a ball is drawn from it
- Find the probability that the ball is white
- If the ball is white, what is the probability that it from the first box?
![]()
Question 47 (a).
If Ai Bi, Ci are the cofactors of ai, bi, ci, respectively, i = 1 to 3 in
[OR]
(b) Express the matrix \(\left(\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right)\) as the sum of symmetric martix and a skew-symmetric martix?