Students can Download Tamil Nadu 11th Maths Model Question Paper 4 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
TN State Board 11th Maths Model Question Paper 4 English Medium
General Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer - Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
- Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
- Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.
Time: 2:30 Hours
Maximum Marks: 90
PART – I
I. Choose the correct answer. Answer all the questions: [20 × 1 = 20]
Question 1.
If n(A) = 2 and n(B∪C) = 3 then n[(A × B) ∪ (A × C)] is ………………..
(a) 23
(b) 32
(c) 6
(d) 5
Answer:
(c) 6
![]()
Question 2.
For any two sets A and B, A∩(A∪B) = …………………….
(a) B
(b) ∅
(c) A
(d) none of these
Answer:
(c) A
Question 3.
cos 1° + cos 2° + cos 3° + cos 4° + cos 179° = …………………
(a) 0
(b) 1
(c) -1
(d) 89
Answer:
(a) 0
![]()
Question 4.
The value of log9 27 is ……………………
(a) \(\frac{2}{3}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{4}{3}\)
Answer:
(b) \(\frac{3}{2}\)
Question 5.
The value of \(\frac{\sin 3 \theta+\sin 5 \theta+\sin 7 \theta+\sin 9 \theta}{\cos 3 \theta+\cos 5 \theta+\cos 7 \theta+\cos 9 \theta}\) = ………………..
(a) tan3θ
(b) tan6θ
(c) cot3θ
(d) cot6θ
Answer:
(b) tan6θ
Question 6.
In 3 fingers the number of ways 4 rings can be worn in ……………………. ways.
(a) 43 – 1
(b) 34
(c) 68
(d) 64
Answer:
(d) 64
![]()
Question 7.
Everybody in a room shakes hands with everybody else. The total number of shake hands is 66. The number of persons in the room is ……………….
(a) 11
(b) 12
(c) 10
(d) 6
Answer:
(b) 12
Question 8.
The H.M of two positive number whose AM and G.M. are 16, 8 respectively is ………………..
(a) 10
(b) 6
(c) 5
(d) 4
Answer:
(d) 4
![]()
Question 9.
The co-efficient of the term independent of x in the expansion of (2x+\(\frac{1}{3x}\))6 is …………………
(a) \(\frac{160}{27}\)
(b) \(\frac{160}{27}\)
(c) \(\frac{80}{3}\)
(d) \(\frac{80}{9}\)
Answer:
(a) \(\frac{160}{27}\)
Question 10.
The value of \(\left|\begin{array}{lll}
a & 0 & 0 \\
0 & b & 0 \\
0 & 0 & c
\end{array}\right|^{2}\) is ………………..
(a) abc
(b) -abc
(c) 0
(d) a2b2c2
Answer:
(d) a2b2c2
![]()
Question 11.
The value of x for which the matrix A = \(\left[\begin{array}{cc}
e^{x-2} & e^{7+x} \\
e^{2+x} & e^{2 x+3}
\end{array}\right]\) is singular is …………………..
(a) 9
(b) 8
(c) 7
(d) 6
Answer:
(b) 8
Question 12.
If |\(\vec { a } \) + \(\vec { b } \)| = 60, |\(\vec { a } \) – \(\vec { b } \)| = 40 and |\(\vec { b } \)| = 46 then |\(\vec { a } \)| is …………………
(a) 42
(b) 12
(c) 22
(d) 32
Answer:
(c) 22
![]()
Question 13.
Given \(\vec { a } \) = 2\(\vec { i } \) + \(\vec { j } \) – 8\(\vec { k } \) and \(\vec { b } \) = \(\vec { i } \) + 3\(\vec { j } \) – 4\(\vec { k } \) then |\(\vec { a } \) + \(\vec { b } \)| = ………………….
(a) 13
(b) \(\frac{13}{3}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{3}{13}\)
Answer:
(a) 13
Question 14.
If f(x) = \(\left\{\begin{array}{ccc}
k x & \text { for } & x \leq 2 \\
3 & \text { for } & 2
\end{array}\right.\) is continous at x = 2 then the value of k is ……………………
(a) \(\frac{3}{4}\)
(b) 0
(c) 1
(d) \(\frac{4}{3}\)
Answer:
(c) 1
![]()
Question 15.
If f: R→R is defined by f(x) = |x – 3| + |x – 4| for x∈R then \(\lim _{x \rightarrow 3^{-}}\) f(x) is equal to ………………..
(a) -2
(b) -1
(c) 0
(d) 1
Answer:
(c) 0
Question 16.
\(\lim _{x \rightarrow \infty}\left(\frac{x^{2}+5 x+3}{x^{2}+x+3}\right)^{x}\) is ………………..
(a) e4
(b) e2
(c) e3
(d) 1
Answer:
(a) e4
![]()
Question 17.
\(\int \frac{e^{x}\left(x^{2} \tan ^{-1} x+\tan ^{-1} x+1\right)}{x^{2}+1}\) dx is ………………..
(a) e tan-1(x + 1)
(b) tan-1(ex) + c
(c) ex \(\frac{\left(\tan ^{-1} x\right)^{2}}{2}\) + c
(d) extan-1x + c
Answer:
(d) extan-1x + c
Question 18.
∫ \(\frac { secx }{ \sqrt { cos2x } } \) dx = …………………..
(a) tan-1(sin x) + c
(b) 2 sin-1(tan x) + c
(c) tan-1(cos x) + c
(d) sin-1 (tan x) + c
Answer:
(d) sin-1 (tan x) + c
![]()
Question 19.
\(\int \frac{e^{6 \log x}-e^{5 \log x}}{e^{4 \log x}-e^{3 \log x}}\) dx = ………………..
(a) x + c
(b) \(\frac { x^{ 3 } }{ 3 } \) + c
(c) \(\frac { 3 }{ x^{ 3 } } \) + c
(d) \(\frac { 1 }{ x^{ 2 } } \) + c
Answer:
(b) \(\frac { x^{ 3 } }{ 3 } \) + c
Question 20.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\), P(B/A) = \(\frac{2}{3}\) then P(B) = …………………
(a) \(\frac{1}{6}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{2}\)
Answer:
(b) \(\frac{1}{3}\)
PART – II
II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]
Question 21.
In the set Z of integers, define mRn if m – n is a multiple of 12. Prove that R is an equivalence relation?
Answer:
As m – m = 0 and 0 = 0 × 12, we have 0 is a multiple of 12; hence mRm proving that R is reflexive.
Let mRn. Then m – n = 12k for some integer k; thus n – m = 12(-k) and hence nRm.
This shows that R is symmetric.
Let mRn and nRp: then m – n = 12k and n – p = 12l for some integers k and l.
So m – p = 12(k + l) and hence mRp. This shows that R is transitive.
Thus R is an equivalence relation.
![]()
Question 22.
Simplify:
\(\frac { 1 }{ 2+\sqrt { 3 } } \) + \(\frac { 3 }{ 4-\sqrt { 5 } } \) + \(\frac { 6 }{ 7-\sqrt { 8 } } \)
Answer:

Question 23.
Find the value of sin 22 \(\frac{1}{2}\)°?
Answer:
We know that cos θ = 1 – 2 sin2 \(\frac{θ}{2}\) ⇒ sin \(\frac{θ}{2}\) = ±\(\sqrt { \frac { 1-cos2\theta }{ 2 } } \)
Take θ = 45°, we get sin \(\frac{45°}{2}\) = ±\(\sqrt { \frac { 1-cos45°}{ 2 } } \), (taking positive sign only, since 22\(\frac{1}{2}\)° lies in the first quadrant)
Thus, sin 22\(\frac{1}{2}\)° = \(\sqrt{\frac{1-\frac{1}{\sqrt{2}}}{2}}=\frac{\sqrt{2-\sqrt{2}}}{2}\).
![]()
Question 24.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th
hour and wth hour?
Answer:
No. of bacteria at the beginning = 30
No. of bacteria after 1 hour = 30 × 2 = 60
No. of bactena after 2 hours = 30 × 22 = 30 × 4 = 120
No. of bacteria after 4 hours = 30 × 24 = 30 × 16 = 480
No. of bacteria after nth hour = 30 × 2n
![]()
Question 25.
If the sum of the distance of a moving point in a plane from the axis is 1, then find the locus of the point?
Answer:
Let coordinates of a moving point P be (x, y).
Given that the sum of the distances from the axis to the point is always 1.
∴|x| + |y| = 1 ⇒ x + y = 1
⇒- x- y = 1 ⇒ x + y = 1
⇒ x – y = 1
Hence, these equations give us the locus of the point P which is a square.

Question 26.
If (a, a + b, a + b + c) is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0) then find a set of values of a, b, c?
Answer:
Let A be the point (1, 0, 0) and B be the point (0, 1, 0) (i.e.,) \(\overline { OA } \) = \(\hat { i } \) and \(\overline { OB } \) = \(\hat { j } \).
Then \(\overline { AB } \) = \(\overline { OB } \) – \(\overline { OA } \) = \(\hat { j } \) – \(\hat { i } \) = –\(\hat { i } \) + \(\hat { j } \)
= (-1, 1, 0)
= (a, a + b, a + b + c)
⇒ a = -1, a + b = 1 and a + b + c = 0
⇒ a = -1, ⇒ -1 + b = 1; a + b + c = 0
⇒ b = 2; -1 + 2 + c = 0 ⇒ c + 1 = 0
⇒ c = -1
∴ a = -1, b = 2, c = -1.
Note: if we taken \(\overline { BA } \) then we get a = 1, b = -2 and c = 1.
![]()
Question 27.
Find \(\frac{dy}{dx}\) for y = (x2 + 4x + 6)5
Answer:
Let u = x2 + 4x + 6
⇒ \(\frac{du}{dx}\) = 2x + 4
Now y = u5 = \(\frac{dy}{du}\) = 5u4
∴ \(\frac{dy}{dx}\) = \(\frac{dy}{du}\) × \(\frac{du}{dx}\) = 5u4 (2x + 4)
= 5(x2 + 4x + 6)4 (2x + 4)
= 5(2x + 4) (x2 + 4x + 6)4
Question 28.
Evaluate ∫\(\sqrt { 25x^{ 2 }-9 } \) dx?
Answer:
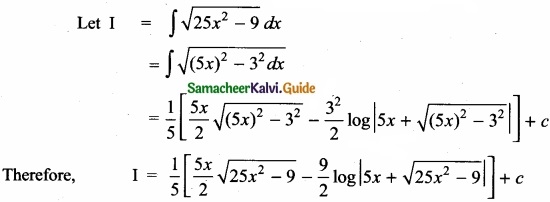
Question 29.
A bag contains 5 white and 7 black balls. 3 balls are drawn at random. Find the probability that
- all are white
- one white and 2 black.
Answer:
Number of white balls = 5
Number of black balls = 7
Total number of balls = 12
Selecting 3 from 12 balls can be done in
12C3 = \(\frac{12 \times 11 \times 10}{3 \times 2 \times 1}\) = 220 ways
∴n(S) = 220
1. Let A be the selecting 3 white balls.
∴n(A) = 5C3 = 5C2 = \(\frac{5×3}{2×1}\) = 10
∴P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{10}{220}\) = \(\frac{1}{22}\)
2. Let B be the event of selecting one white and 2 black balls.
∴n(B) = 5C1 × 7C2 = (5) (\(\frac{7×6}{2×1}\)) = 5(21) = 105
∴P(B) = \(\frac{n(B)}{n(S)}\) = \(\frac{105}{220}\) = \(\frac{21}{44}\).
![]()
Question 30.
If (k, 2), (2, 4) and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k?
Answer:
Area of ∆ with vertices (k, 2) (2, 4) and (3, 2) = \(\frac{1}{2}\) \(\left|\begin{array}{lll}
k & 2 & 1 \\
2 & 4 & 1 \\
3 & 2 & 1
\end{array}\right|\) = 4 given
⇒ \(\left|\begin{array}{lll}
k & 2 & 1 \\
2 & 4 & 1 \\
3 & 2 & 1
\end{array}\right|\) = 2(4) = 8
(i.e.,) k(4 – 2) – 2(2 – 3) + 1(4 – 12) ± 8
(i.e.,) 2k – 2(-1) + 1(-8) = ± 8
(i.e.,) 2k + 2 – 8 = 8
(i.e.,) 2k = 8 + 8 – 2 = 14
k = 14/2 = 7
∴k = 7
So k = 7 (or) k = -1.
2k + 2 – 8 = -8
⇒2k = – 8 + 8 – 2
2k = – 2
k = -1
PART – III
III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]
Question 31.
In the set Z of integers define mRn if m – n is a multiple of 12. Prove that R is an equivalence relation?
Question 32.
Prove that \(\frac{sin4x+sin2x}{cos4x+cos2x}\) = tan 3x?
![]()
Question 33.
A polygon has 90 diagonals. Find the number of its sides?
Question 34.
If n is an odd positive integer, prove that the coefficients of the middle terms in the expansion of (x + y)n are equal?
Question 35.
Find the equation of the line passing through the point (1, 5) and also divides the co-ordinate axes in the ratio 3 : 10?
![]()
Question 36.
Prove that \(\left|\begin{array}{ccc}
1 & x & x \\
x & 1 & x \\
x & x & 1
\end{array}\right|^{2}=\left|\begin{array}{ccc}
1-2 x^{2} & -x^{2} & -x^{2} \\
-x^{2} & -1 & x^{2}-2 x \\
-x^{2} & x^{2}-2 x & -1
\end{array}\right|\)
Question 37.
If G is the centroid of a traiangle ABC prove that \(\overline { GA } \) + \(\overline { GB } \) + \(\overline { GC } \) = 0
![]()
Question 38.
Find \(\frac{dy}{dx}\) for y = \(\sqrt { 1+tan2x } \)?
Question 39.
Evaluate \(\frac { \sqrt { x } }{ 1+\sqrt { x } } \) dx?
Question 40.
Find the relation between a and b if \(\underset { x\rightarrow 3 }{ lim } \) f(x) exists where f(x) = \(\left\{\begin{array}{cc}
a x+b & \text { if } x>3 \\
3 a x-4 b+1 \text { if } x<3
\end{array}\right.\)
PART – IV
IV. Answer all the questions. [7 × 5 = 35]
Question 41 (a).
From the curve y = |x|, draw(i) y = |x-1| + 1
- y = |x + 1| + 1
- y = |x + 2| – 3
[OR]
(b) Resolve into partial fraction \(\frac { x+4 }{ (x^{ 2 }-4)(x+1) } \)
![]()
Question 42 (a).
Find the number of positive integers greater than 6000 and less than 7000 which arc divisible by 5, provided that no digit is to be repeated?
[OR]
(b) If nPr = nPr+1 and nCr = nCr-1, find the values of n and r?
Question 43 (a).
In a ∆ABC, prove that b2 sin 2C + c2 sin 2B = 2bc sin A?
[OR]
(b) Differentiate the following s(t) = \(\sqrt[4]{\frac{t^{3}+1}{t^{3}-1}}\)?
![]()
Question 44 (a).
Find the equation of the lines make an angle 60° with the positive x axis and at a distance 5\(\sqrt{2}\) units measured from the point (4, 7) along the line x – y + 3 = 0
[OR]
(b) If y = A cos4x + B sin 4x, A and B are constants then Show that y2 + 16y = 0
![]()
Question 45 (a).
Find the sum up to the 17th term of the series \(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\frac{1^{3}+2^{3}+3^{3}}{1+3+5}\) + …………..
[OR]
(b) A shopkeeper in a Nuts and Spices shop makes gifi packs of cashew nuts, raisins and almonds?
- Pack I contains 100 gm of cashew nuts, 100 gm of raisins and 50 gm of almonds.
- Pack-II contains 200 gm of cashew nuts, 100 gm of raisins and 100 gm of almonds.
- Pack-III contains 250 gm of cashew nuts, 250 gm of raisins and 150 gm of almonds.
- The cost of 50 gm of cashew nuts is ₹50, 50 gm of raisins is ₹10. and 50gm of almonds is ₹60. What is the cost of each gift pack?
![]()
Question 46 (a).
Find matrix C if A = \(\begin{bmatrix} 3 & 7 \\ 2 & 5 \end{bmatrix}\), B = \(\begin{bmatrix} -3 & 2 \\ 4 & -1 \end{bmatrix}\) and 5C + 28= A?
[OR]
(b) The probability that a new railway bridge will get an award for its design is 0.48, the probability that it will get an award for the efficient use of materials is 0.36, and that it will get both awards is 0.2. What is the probability, that
- it will get at least one of the two awards
- it will get only one of the awards.
![]()
Question 47 (a).
\(\underset { \alpha \rightarrow 0 }{ lim } \) \(\frac { sin(\alpha ^{ n }) }{ (sin\alpha )^{ m } } \)
[OR]
(b) Evaluate I = sin-1 (\(\frac { 2x }{ (1+x)^{ 2 } } \)) dx?