Students can Download Tamil Nadu 12th Physics Model Question Paper 1 English Medium Pdf, Tamil Nadu 12th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
TN State Board 12th Physics Model Question Paper 1 English Medium
General Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III, and IV are to be attempted separately.
- Question numbers 1 to 15 in Part I are Multiple Choice Questions of one mark each.
These are to be answered by choosing the most suitable answer from the given four
alternatives and writing the option code and the corresponding answer - Question numbers 16 to 24 in Part II are two-mark questions. These are to be answered
in about one or two sentences. - Question numbers 25 to 33 in Part III are three-mark questions. These are to be answered
in about three to five short sentences. - Question numbers 34 to 38 in Part IV are five-mark questions. These are to be answered
in detaiL Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 70
Part – I
Answer all the questions. Choose the correct answer. [15 x 1 = 15]
Question 1.
Two points A and B are maintained at a potential of 7 V and -4 V respectively. The work done in moving 50 electrons from A to B is …………….
(a) 80 x 10-17 J
(b) -8.80 x 10-17 J
(c) 4.40 x 10-17 J
(d) 5.80 x 10-17 J
Answer:
(a) 80 x 10-17 J
Question 2.
The following graph shows current versus voltage values of some unknown conductor. What is the resistance of this conductor?
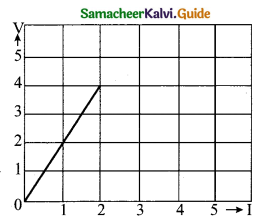
(a) 2 ohm
(b) 4 ohm
(c) 8 ohm
(d) 1 ohm
Answer:
(a) 2 ohm
Question 3.
Two identical coils, each with N turns and radius R are placed coaxially at a distance R as shown in the figure. If I is the current passing through the loops in the same direction, then the magnetic field at a point P which is at exactly at R/2 distance between two coils is …………..

Answer:
![]()
Question 4.
An electron moves on a straight line path XY as shown in the figure. The coil abed is adjacent to the path of the electron. What will be the direction of current, if any, induced in the coil?
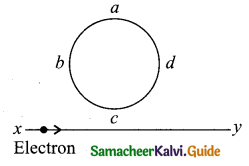
(a) The current will reverse its direction as the electron goes past the coil
(b) No current will be induced
(c) abcd
(d) adcb
Answer:
(a) The current will reverse its direction as the electron goes past the coil
Question 5.
The resistance of an ideal ammeter is ……………
(a) zero
(b) small
(c) high
(d) infinite
Answer:
(a) zero
Question 6.
In a step-down transformer the input voltage is 22 kV and the output voltage is 550 V. The ratio of the number of turns in the secondary to that in the primary is ……………
(a) 1 : 20
(b) 20 : 1
(c) 1 : 40
(d) 40 : 1
Answer:
(c) 1 : 40
![]()
Question 7.
If the magnetic monopole exists, then which of the Maxwell’s equation to be modified?
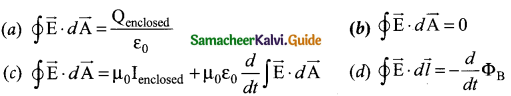
Answer
\(\oint \overrightarrow { { E } } \cdot d\overrightarrow { { A } } =0\)
Question 8.
An air bubble in glass slab of refractive index 1.5 (near normal incidence) is 5 cm deep when viewed from one surface and 3 cm deep when viewed from the opposite face. The thickness of the slab is,
(a) 8 cm
(b) 10 cm
(c) 12 cm
(d) 16 cm
Answer:
(c) 12 cm
Hint. Let d1 = 5 cm and d2 = 3 cm ; n = 1.5
Actual width is the sum of real depth from 2 sides
Thickness of slab = d1n + d2n
= (5 x 1.5) +(3 x 1.5)= 12 cm
Question 9.
When a ray of light enters a glass slab from air
(a) its wavelength decreases
(b) its wavelength increases
(c) its frequency increases
(d) neither its wavelength nor its frequency changes
Answer:
(a) its wavelength decreases
Hint: \(Wavelength,\lambda =\frac { { Velocity } }{ { Frequency } } =\frac { u }{ v } \)
When light travels from air to glass, frequency ν remains unchanged, velocity u decreases and hence wave length λ also decreses
![]()
Question 10.
A particle of mass 3 x 10-6 g has the same wavelength as an electron moving with a velocity
6 x 106 m s-1. The velocity of the particle is…………………………………………
(a) 1.82 x 10-18 ms-1
(b) 9 x 10-2 ms-1
(c) 3 x 10-31 ms-1
(d) 1.82 x 1015 ms-1
Answer:
(d) 1.82 x 1015 ms-1
Hint: de – Broglie wavelength of electron
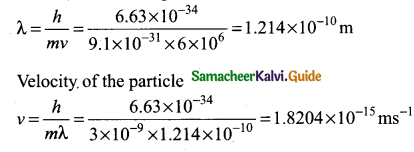
Question 11.
If the nuclear radius of 27A1 is 3.6 fermi, the approximate unclear radius of 64Cu is
(a) 2.4
(b) 1.2
(c) 4.8
(d) 3.6
Answer:
(c) 4.8
Hint :

Question 12.
Energy of characteristic X-ray is a consequence of ………….
(a) energy of projectile electron
(b) thermal energy of target
(c) transition in target atoms
(d) none of the above
Answer:
(c) transition in target atoms
Question 13.
The specific characteristic of a common emitter amplifier is ……………
(a) High input resistance
(b) Low power gain
(c) Signal phase reversal
(d) Low current gain
Answer:
(c) Signal phase reversal
Question 14.
The variation of frequency of carrier wave with respect to the amplitude of the modulating signal is called ………………
(a) Amplitude modulation
(b) Frequency modulation
(c) Phase modulation
(d) Pulse width modulation
Answer:
(b) Frequency modulation
![]()
Question 15.
The particle size of ZnO material is 30 nm. Based on the dimension it is classified as ……………..
(a) Bulk material
(b) Nanomaterial
(c) Soft material
(d) Magnetic material
Answer:
(b) Nanomaterial
Part – II
Answer any six questions in which Q. No 17 is compulsory. [6 x 2 = 12]
Question 16.
Write a short note on the superposition principle.
Answer:
According to this superposition principle, the total force acting on a given charge is equal to the vector sum of forces exerted on it by all the other charges.
\(\overrightarrow{\mathrm{F}}_{1}^{\mathrm{tot}}=\overrightarrow{\mathrm{F}}_{12}+\overrightarrow{\mathrm{F}}_{13}+\overrightarrow{\mathrm{F}}_{14}+\cdots+\overrightarrow{\mathrm{F}}_{1 n}\)
Question 17.
If an electric field of magnitude 570 N C-1, is applied in the copper wire, find the acceleration experienced by the electron.
Answer:
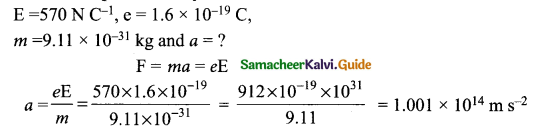
Question 18.
State Ampere’s circuital law.
Answer:
The line integral of magnetic field over a closed loop is p0 times net current enclosed by the loop.
\(\oint_{C} \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_{0} \mathrm{I}_{\text {enclosed }}\)
Question 19.
Write down the equation for a sinusoidal voltage of §0 Hz and its peak value is 20 V. Draw the corresponding voltage versus time graph.
Answer:

Question 20.
What is displacement current?
Answer:
The displacement current can be defined as the current which comes into play in the region in which the electric field and the electric flux are changing with time.
![]()
Question 21.
Why do clouds appear white?
Answer:
Clouds have large particles like dust and water droplets which scatter light of all colours almost equally. Hence clouds generally appear white.
Question 22.
How many photons per second emanate from a 50 mW laser of 640 nm?
Answer:
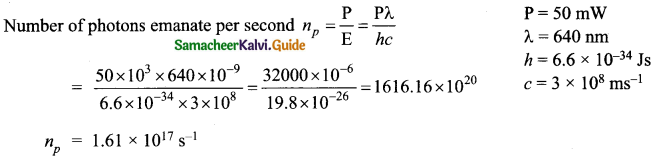
Question 23.
An ideal diode and a 5 Ω resistor are connected in series with a 15 V power supply as shown in figure below. Calculate the current that flows through the diode.
Answer:
The diode is forward biased and it is an ideal one. Hence, it acts like a closed switch with no barrier voltage.Therefore, current that flows through the diode can be calculated using Ohm’s law.
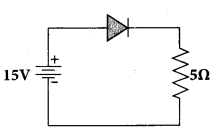
V = IR
\(I=\frac{V}{R}=\frac{15}{5}=3 \mathrm{A}\)
Question 24.
What do you mean by Internet of Things?
Answer:
Internet of Things (IoT), it is made possible to control various devices from a single device. Example: home automation using a mobile phone.
Part – III
Answer any six questions in which Q.No. 26 is compulsory. [6 x 3 = 18]
Question 25.
Define electrostatic potential energy?
Answer:
The potential energy of a system of point charges may be defined as the amount of work done in assembling the charges at their locations by bringing them in from infinity.
Question 26.
If the resistance of coil is 3 Ω at 20°C and a = 0.004/°C then determine its resistance at 100°C.
Answer:
R0 =3Ω = 100°C, T0 = 20°C
α = 0.004/°C, RT = ?
Rr= R0(1+∝ (T-T0))
R100 = 3(1 + 0.004 x 80)
⇒ R100 = 3(1 + 0.32)
R100= 3(1.32)
⇒ R100 = 3.96 Ω
![]()
Question 27.
State ‘Tangent Law’.
Answer:
When a magnetic needle or magnet is freely suspended in two mutually perpendicular uniform magnetic fields, it will come to rest in the direction of the resultant of the two fields.
Question 28.
What are step-up and step-down transformers?
Answer:
If the transformer converts an alternating current with low voltage into an alternating current with high voltage, it is called step-up transformer. On the contrary, if the transformer converts alternating current with high voltage into an alternating current with low voltage, then it is called step-down transformer.
Question 29.
One type of transparent glass has refractive index 1.5. What is the speed of light through this glass?
Answer:
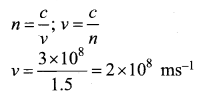
Question 30.
What is a photo cell? Mention the different types of photocells.
Answer:
Photocells: Photo electric cell or photo cell is a device which converts light energy into electrical energy. It works on the principle of photo electric effect.
Types:
- Photo emissive cell
- Photo voltaic cell
- Photo conductive cell
Question 31.
Half lives of two radioactive elements A and B are 20 minutes and 40 minutes respectively. Initially, the samples have equal number of nuclei. Calculate the ratio of decayed numbers of A and B nuclei after 80 minutes.
Answer:
80 minutes = 4 half lives of A = 2 half live of B
Let the initial number of nuclei in each sample be N.

Question 32.
Distinguish between intrinsic and extrinsic semiconductors.
Answer:
| Intrinsic | Extrinsic |
| These are pure semiconducting tetravalent crystals. | These are semiconducting tetravalent crystals doped with impurity atoms group III (or) V |
| Their electrical conductivity is low. | Their electrical conductivity is high. |
| There is no permitted energy state between valence and conduction band. | There is no permitted energy state of the impurity atom between valence and conduction band. |
| Their electrical conductivity depends on temperature. | Their electrical conductivity depends on temperature as well as dopant concentration. |
Question 33.
Distinguish between Nanoscience and Nanotechnology.
Answer:
| Nanoscience | Nanotechnology |
| Nanoscience is the science of objects with typical sizes of 1-100 nm. Nano means one- billionth of a metre that is 10-9 m.
If matter is divided into such small objects the mechanical, electrical, optical, magnetic and other properties change. |
Nanotechnology is a technology involving the design, production, characterization, and applications of nano structured materials. |
Part – IV
Answer all the questions. [5 x 5 = 25]
Question 34.
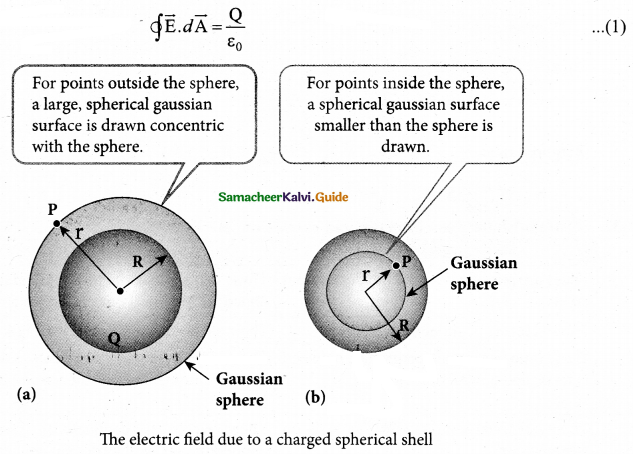
(a) Obtain the expression for electric field due to an uniformly charged spherical shell. Electric field due to a uniformly charged
Answer:
spherical shell: Consider a uniformly charged spherical shell of radius R and total charge Q. The electric field at points outside and inside the sphere is found using Gauss law.
Case (a) At a point outside the shell (r > R): Let us choose a point P outside the shell at a distance r from the center as shown in figure (a). The charge is uniformly distributed on the surface of the sphere (spherical symmetry). Hence the electric field must point radially
outward if Q > 0 and point radially inward if Q < 0. So we choose a spherical Gaussian surface of radius r and the total charge enclosed by this Gaussian surface is Q. Applying Gauss law,
The electric field \(\overrightarrow { { E } } { and }\quad d\overrightarrow { { A } } \) point in the same direction (outward normal) at all the points on the Gaussian surface. The magnitude of \(\overrightarrow { { E } } \) is also the same at all points due to the spherical symmetry of the charge distribution.
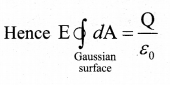
But  = total area of Gaussian surface = 4πr2 Substituting this value in equation (2)
= total area of Gaussian surface = 4πr2 Substituting this value in equation (2)

The electric field is radially outward if Q > 0 and radially inward if Q < 0. From equation (3), we infer that the electric field at a point outside the shell will be same as if the entire charge Q is concentrated at the center of the spherical shell. (A similar result is observed in gravitation, for gravitational force due to a spherical shell with mass M)
![]()
Case (b): At a point on the surface of the spherical shell (r = R): The electrical field at points on the spherical shell (r = R) is given by
\(\overrightarrow{\mathrm{E}}=\frac{Q}{4 \pi \varepsilon_{0} R^{2}} \hat{r}\) ………. (4)
Case (c) At a point inside the spherical shell (r < R): Consider a point P inside the shell at a distance r from the center. A Gaussian sphere of radius r is constructed as shown in the figure (b). Applying Gauss law.

Since Gaussian surface encloses no charge, So Q = 0. The equation (5) becomes
E = 0 (r < R) ………….. (6)
The electric field due to the uniformly charged spherical shell is zero at all points inside the shell.
[OR]
(b) Obtain the condition for bridge balance in Wheatstone’s bridge.
Answer:
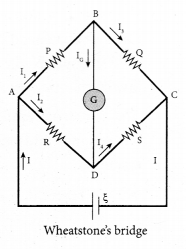
An important application of Kirchhoff’s rules is the Wheatstone’s bridge. It is used to compare resistances and also helps in determining the unknown resistance in electrical network. The bridge consists of four resistances P, Q, R and S connected. A galvanometer G is connected between the points B and D. The battery is connected between the points A and C. The current through the galvanometer is IG and its resistance is G.
Applying Kirchhoff’s current rule to junction B.
I1 – IG – I3 = 0 ………….. (1)
Applying Kirchhoff’s current rule to junction D.
I2 + IG – I4 = 0 ………….. (2)
Applying Kirchhoff’s voltage rule to loop ABDA,
I1P + IGG – I2R = 0 ………….. (3)
Applying Kirchhoff’s voltage rule to loop ABCDA,
I1P + I3Q – I4S – I2R = 0 ………….. (4)
When the points B and D are at the same potential, the bridge is said to be balanced. As there is no potential difference between B through galvanometer (IQ = 0). Substituting IG = 0 in equation, (1), (2) and (3), we get
I1 = I3 ………………….. (5)
I1 = I4 ……………………. (6)
I1P =I2R ……………….(7)
Substituting the equation (5) and (6) in equation (4)
I1P + I1Q – I1S – I1R = 0
I1( P + Q) = I2( P + S) …………………(8)
Dividing equation (7)
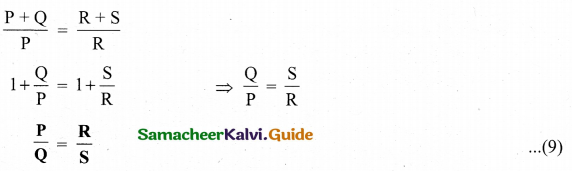
This is the bridge balance condition. Only under this condition, galvanometer shows null deflection. Suppose we know the values of two adjacent resistances, the other two resistances can be compared. If three of the resistances are known, the value of unknown resistance (fourth one) can be determined.
Question 35.
(a) Obtain the magnetic induction at a point on the equatorial line of a bar magnet. Magnetic field at a point along the equatorial line due to a magnetic dipole (bar magnet)
Answer:
Consider a bar magnet NS. Let N be the north pole and S be the south pole of the bar magnet, each with pole strength qm and separated by a distance of 21. The magnetic field at a point C (lies along the equatorial line) at a distance r from the geometrical center O of the bar magnet can be computed by keeping unit north pole (qmC = 1 A m) at C. The force experienced by the unit north pole at C due to pole strength N-S can be computed using Coulomb’s law of magnetism as follows:
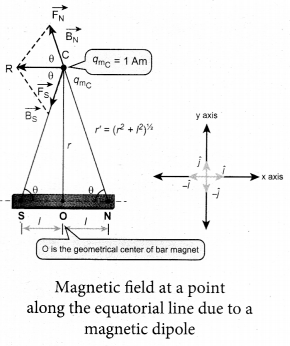
The force of repulsion between North Pole of the bar magnet and unit north pole at point C (in free space) is
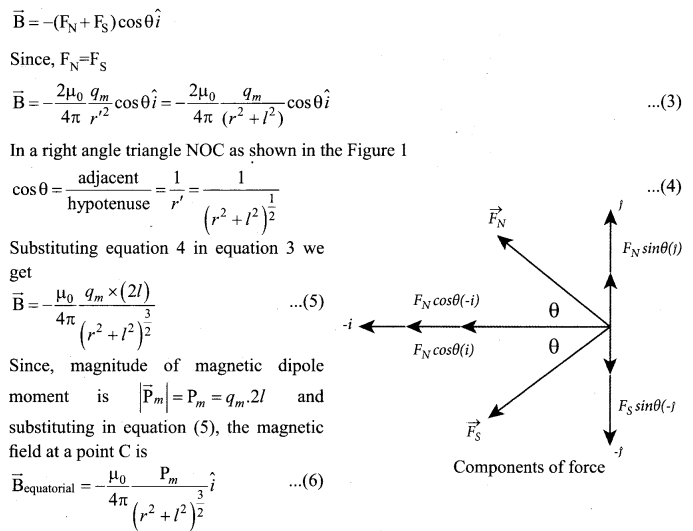
\(\overrightarrow{\mathrm{F}}_{\mathrm{N}}=-\mathrm{F}_{\mathrm{N}} \cos \theta \hat{i}+\mathrm{F}_{\mathrm{N}} \sin \theta \hat{j}\) ……………. (1)
Where \(\overrightarrow{\mathrm{F}}_{\mathrm{S}}=\frac{\mu_{0}}{4 \pi} \frac{q_{m}}{r^{\prime 2}}\) . The force of attraction (in free space) between south pole of the bar magnet and unit north pole at point C is

From equation (1) and equation (2), the net force at point C is \(\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{F}}_{\mathrm{N}}+\mathrm{F}_{\mathrm{S}}\). This net force is equal to the magnetic field at the point C.
If the distance between two poles in a bar magnet are small (looks like short magnet) when compared to the distance between geometrical center O of bar magnet and the location of point C i.e., r>> l, then,

Therefore , using equation (7) in equation (6) ,we get
\(\overrightarrow{\mathrm{B}}_{\text {equatorial }}=-\frac{\mu_{0}}{4 \pi} \frac{p_{m}}{r^{3}} \hat{i}\)
Since in genaral , the magnetic filed at equatorial points is given by

Note that magnitude of Baxial is twice that of magnitude of Bequatoral and the direction of Baxial and Bequatoral are opposite.
![]()
[OR]
Question 35.
(b) Give the advantage of AC in long distance power transmission with an example.
Answer:
Advantages of AC in long distance power transmission: Electric power is produced in a large scale at electric power stations with the help of AC generators. These power stations are classified based on the type of fuel used as thermal, hydro electric and nuclear power stations. Most of these stations are located at remote places. Hence the electric power generated is transmitted over long distances through transmission lines to reach towns or cities where it is actually consumed. This process is called power transmission.
But there is a difficulty during power transmission. A sizable fraction of electric power is lost due to Joule heating (i2R) in the transmission lines which are hundreds of kilometer long. This power loss can be tackled either by reducing current I or by reducing resistance R of the transmission lines. The resistance R can be reduced with thick wires of copper or aluminium. But this increases die cost of production of transmission lines and other related expenses. So this way of reducing power loss is not economically viable.
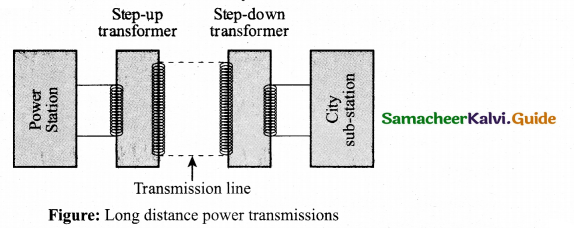
Since power produced is alternating in nature, there is a way out. The most important property of alternating voltage is that it can be stepped up and stepped down by using transformers could be exploited in reducing current and thereby reducing power losses to a greater extent. At the transmitting point, the voltage is increased and the corresponding current is decreased by using step-up transformer.
Then it is transmitted through transmission lines. This reduced current at high voltage reaches the destination without any appreciable loss. At the receiving point, the voltage is decreased and the current is increased to appropriate values by using step-down transformer and then it is given to consumers. Thus power transmission is done efficiently and economically.
Illustration: An electric power of 2 MW is transmitted to a place through transmission lines of total resistance, say R = 40 Ω, at two different voltages. One is lower voltage (10 kV) and the other is higher (100 kV). Let us now calculate and compare power losses in these two cases.
Case (i) : P = 2 MW; R = 40 Ω; V = 10 kV
Power, P= VI
Power loss = Heat produced = I2R = (200)2 x 40 = 1.6 x 106 W
% of power loss = \(\frac{1.6 \times 10^{6}}{2 \times 10^{6}} \times 100 \%\) = 0.8 x 100% = 80%
![]()
Case (ii): P = 2 MW; R = 40 Ω; V = 100 kV
∴ Current, \(I=\frac{P}{V}=\frac{2 \times 10^{6}}{100 \times 10^{3}}=20 \mathrm{A}\)
Power loss = Heat produced = I2R = (20)2 x 40 = 0.016 x 106 W
% of power loss = \(\frac{0.016 \times 10^{6}}{2 \times 10^{6}} \times 100 \%=\) = 0.008 x 100% = 0.8%
Question 36.
(a) What is emission spectra? Give their types.
Answer:
Emission spectra: When the spectrum of self luminous source is taken, we get emission spectrum. Each source has its own characteristic emission spectrum. The emission spectrum can be divided into three types:
(i) Continuous emission spectra (or continuous spectra): If the light from incandescent lamp (filament bulb) is allowed to pass through prism (simplest spectroscope), it splits into seven colours. Thus, it consists of wavelengths containing all the visible colours ranging from violet to red. Examples: spectrum obtained from carbon arc, incandescent solids, liquids gives continuous spectra.

(ii) Line emission spectrum (or line spectrum): Suppose light from hot gas is allowed to pass through prism, line spectrum is observed. Line spectra are also known as discontinuous spectra. The line spectra are sharp lines of definite wavelengths or frequencies. Such spectra arise due to excited atoms of elements. These lines are the characteristics of the element which means it is different for different elements. Examples: spectra of atomic hydrogen, helium, etc

(iii) Band emission spectrum (or band spectrum): Band spectrum consists of several number of very closely spaced spectral lines which overlapped together forming specific bands which are separated by dark spaces, known as band spectra. This spectrum has a sharp edge at one end and fades out at the other end. Such spectra arise when the molecules are excited. Band spectrum is the characteristic of the molecule hence, the structure of the molecules can be studied using their band spectra. Examples, spectra of hydrogen gas, ammonia gas in the discharge tube etc.
[OR]
(b) Obtain the equation for radius of illumination (or) Snell’s window.
Answer:
The radius of Snell’s window can be deduced with the illustration as shown in figure. Light is seen from a point A at a depth d. The Snell’s law in product form, equation n2 sin i = n2 sin r for the refraction happening at the point B on the boundary between the two media is,
n1 sin ic = n2 sin 90° ………………. (1)
n1 sin ic = n2
∵ sin 90° = 1
sin ic = \(\frac{n_{2}}{n_{1}}\) ………………….(2)
From the right angle triangle ΔABC,

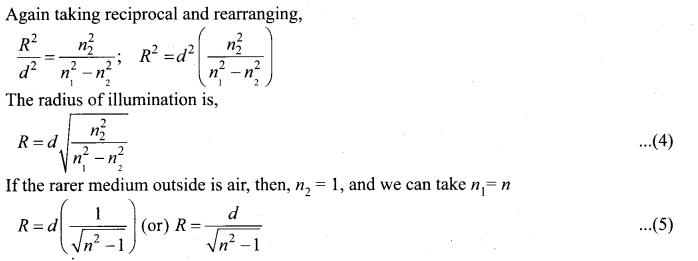
Question 37.
(a) Explain why photoelectric effect cannot be explained on the basis of wave nature of light.
Failures of classical wave theory:
Answer:
From Maxwell’s theory, light is an electromagnetic wave consisting of coupled electric and magnetic oscillations that move with the speed of light and exhibit typical wave behaviour. Let us try to explain the experimental observations of photoelectric effect using wave picture of light.
When light is incident on the target, there is a continuous supply of energy to the electrons. According to wave theory, light of greater intensity should impart greater kinetic energy to the liberated electrons (Here, Intensity of light is the energy delivered per unit area per unit time). But this does not happen. The experiments show that maximum kinetic energy of the photoelectrons does not depend on the intensity of the incident light.
![]()
According to wave theory, if a sufficiently intense beam of light is incident on the surface, electrons will be liberated from the surface of the target, however low the frequency of the radiation is. From the experiments, we know that photoelectric emission is not possible below a certain minimum frequency. Therefore, the wave theory fails to explain the existence of threshold frequency.
Since the energy of light is spread across the wavefront, the electrons which receive energy from it are large in number. Each electron needs considerable amount of time (a few hours) to get energy sufficient to overcome the work function and to get liberated from the surface. But experiments show that photoelectric emission is almost instantaneous process (the time lag is less than 10-9 s after the surface is illuminated) which could not be explained by wave theory.
[or]
(b) Obtain the law of radioactivity.
Answer:
Law of radioactive decay:
At any instant t, the number of decays per unit time, called rate of decay \(\left(\frac{d \mathrm{N}}{d t}\right) \) to the number of nuclei at the same instant.
\(\frac{d \mathrm{N}}{d t} \propto \mathrm{N}\)
By introducing a proportionality constant, the relation can be written as
\(\frac{d \mathrm{N}}{d t}=-\lambda \mathrm{N}\) ……………………. (1)
Here proportionality constant X is called decay constant which is different for different radioactive sample and the negative sign in the equation implies that the N is decreasing with time. By rewriting the equation (1), we get
dN = -XNdt …………… (2)
Here dN represents the number of nuclei decaying in the time interval dt. Let us assume that at time t = 0 s, the number of nuclei present in the radioactive sample is No. By integrating the equation (2), we can calculate the number of undecayed nuclei N at any time t.
From equation (2), we get
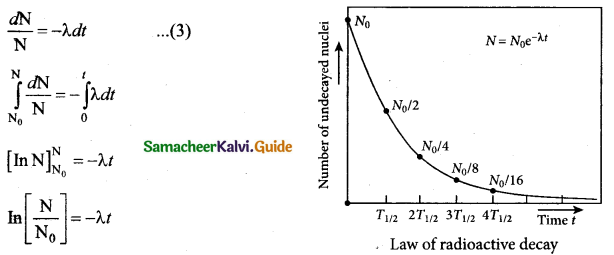
N = No e-λt …………… (4)
[Note: elnx = ey ⇒ x = ey ]
Equation (4) is called the law of radioactive decay. Here N denotes the number of undecayed nuelei present at any time t and N0 denotes the number of nuclei at initial time t = 0. Note that the number of atoms is decreasing exponentially over the time. This implies that the time taken for all the radioactive nuclei to decay will be infinite. Equation (4) is plotted.
We can also define another useful quantity called activity (R) or decay rate which is the number of nuclei decayed per second and it is denoted as R = \(R=\left| \frac { dN }{ dt } \right| \)
Note : That activity R is a positive quantity. From equation (4), we get.

The equation (6) is also equivalent to radioactive law of decay. Here R0 is the activity of the sample at t = 0 and R is the activity of the sample at any time t. From equation (6), activity also shows exponential decay behavior. The activity R also can be expressed in terms of number of undecayed atoms present at any time t. From equation (6), since N = N0 e -λt we write
R = λN ………………… (7)
Equation (4) implies that the activity at any time t is equal to the product of decay constant and number of undecayed nuclei at the same time t. Since N decreases over time, R also decreases.
![]()
Question 38.
(a) Explain the construction and working of a full wave rectifier.
Answer:
Full wave rectifier:
The positive and negative half cycles of the AC input signal pass through the full wave rectifier circuit and hence it is called the full wave rectifier. It consists of two p-n junction diodes, a center tapped transformer, and a load resistor (RL). The centre is usually taken as the ground or zero voltage reference point. Due to the centre tap transformer, the output voltage rectified by each diode is only one half of the total secondary voltage.
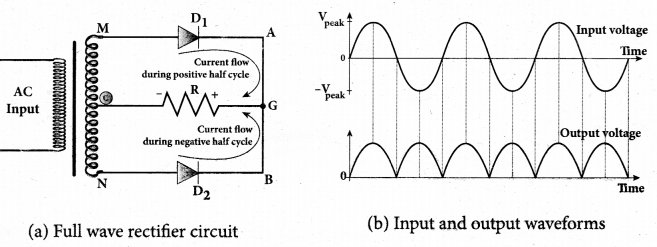
During positive half cycle:
When the positive half cycle of the ac input signal passes through the circuit, terminal M is positive, G is at zero potential and N is at negative potential. This forward biases diode D1 and reverse biases diode D2. Hence, being forward biased, diode D1 conducts and current flows along the path MD1 AGC As a result, positive half cycle of the voltage appears across RL in the direction G to C.
During negative half cycle:
When the negative half cycle of the ac input signal passes through the circuit, terminal N is positive, G is at zero potential and M is at negative potential. This forward biases diode D, and reverse biases diode Dr Hence, being forward biased, diode D2 conducts and current flows along the path ND2 BGC. As a result, negative half cycle of the voltage appears across RL in the same direction from G to C
Hence in a full wave rectifier both positive and negative half cycles of the input signal pass through the circuit in the same direction as shown in figure Though both positive and negative half cycles of ac input are rectified, the output is still pulsating in nature. The efficiency (r|) of full wave rectifier is twice that of a half wave rectifier and is found to be 81.2 %. It is because both the positive and negative half cycles of the ac input source are rectified.
![]()
[OR]
(b) Explain the three modes of propagation of electromagnetic waves through space. Propagation of electromagnetic waves:
Answer:
The electromagnetic wave transmitted by the transmitter travels in three different modes to reach the receiver-according to its frequency range:
(i) Ground wave propagation (or) surface wave propagation (nearly 2 kHz to 2 MHz)
(ii) Sky wave propagation (or) ionospheric propagation (nearly 3 MHz to 30 MHz)
(iii) Space wave propagation (nearly 30 MHz to 400 GHz)
(i) Ground wave propagation
If the electromagnetic waves transmitted by the transmitter glide over the surface of the earth to reach the receiver, then the propagation is called ground wave propagation. The corresponding waves are called ground waves or surface waves.
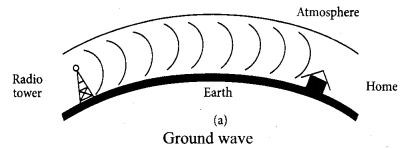
Increasing distance: The attenuation of the signal depends on
- power of the transmitter
- frequency of the transmitter, and
- condition of the earth surface.
Absorption of energy by the Earth: When the transmitted signal in the form of EM wave is in contact with the Earth, it induces charges in the Earth and constitutes a current. Due to this, the earth behaves like a leaky capacitor which leads to the attenuation of the wave.
Tilting of the wave: As the wave progresses, the wavefront starts gradually tilting according to the curvature of the Earth. This increase in the tilt decreases the electric field strength of the wave. Finally, at some distance, the surface wave dies out due to energy loss.
The frequency of the ground waves is mostly less than 2 MHz as high frequency waves undergo more absorption of energy at the earth’s atmosphere. The medium wave signals received during the day time use surface wave propagation.
It is mainly used in local broadcasting, radio navigation, for ship-to-ship, ship-to-shore communication and mobile communication.
(ii) Sky Wave Propagation:
The mode of propagation in which the electromagnetic waves radiated from an antenna, directed upwards at large angles gets reflected by the ionosphere back to earth is called sky wave propagation or ionospheric propagation. The corresponding waves are called sky waves.
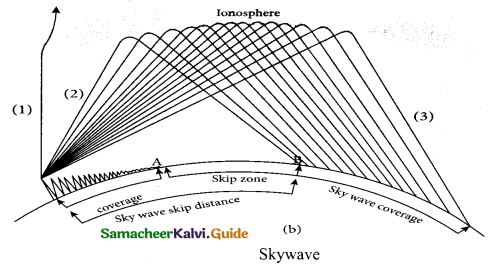
The frequency range of EM waves in this mode of propagation is 3 to 30 MHz. EM waves of frequency more than 30 MHz can easily penetrate through the ionosphere and does not undergo reflection. It is used for short wave broadcast services. Medium and high frequencies are for long-distance radio communication. Extremely long distance communication, is also possible as the radio waves can undergo multiple reflections between the earth and the ionosphere. A single reflection helps the radio waves to travel a distance of approximately 4000 km.
Ionosphere acts as a reflecting surface. It is at a distance of approximately 50 km and spreads up to 400 km above the Earth surface. Due to the absorption of ultraviolet rays, cosmic ray, and other high energy radiations like a, (3 rays from sun, the air molecules in the ionosphere get ionized. This produces charged ions and these ions provide a reflecting medium for the reflection of radio waves or communication waves back to earth within the permitted frequency range. The phenomenon of bending the radio waves back to earth is nothing but the total internal reflection.
![]()
(iii) Space wave propagation:
The process of seeding and receiving information signal through space is called space wave communication. The electromagnetic waves of very high frequencies above 30 MHz are called as space waves. These waves travel in a straight line from the transmitter to the receiver. Hence, it is used for a line of sight communication (LOS).
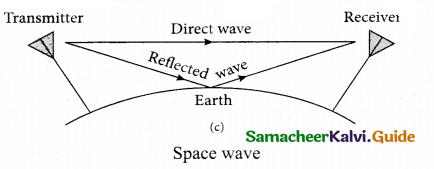
For high frequencies, the transmission towers must be high enough so that the transmitted and received signals (direct waves) will not encounter the curvature of the earth and hence travel with less attenuation and loss of signal strength. Certain waves reach the receiver after getting reflected from the ground.