Students can Download Tamil Nadu 12th Physics Model Question Paper 3 English Medium Pdf, Tamil Nadu 12th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
TN State Board 12th Physics Model Question Paper 3 English Medium
General Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III, and IV are to be attempted separately.
- Question numbers 1 to 15 in Part I are Multiple Choice Questions of one mark each.
These are to be answered by choosing the most suitable answer from the given four
alternatives and writing the option code and the corresponding answer - Question numbers 16 to 24 in Part II are two-mark questions. These are to be answered
in about one or two sentences. - Question numbers 25 to 33 in Part III are three-mark questions. These are to be answered
in about three to five short sentences. - Question numbers 34 to 38 in Part IV are five-mark questions. These are to be answered
in detaiL Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 70
Part – I
Answer all the questions. Choose the correct answer. [15 x 1 = 15]
Question 1.
A thin conducting spherical shell of radius R has a charge Q which is uniformly distributed on its surface. the correct plot for electrostatic potential due to this spherical shell is ………

Answer:
(b)
Question 2.
The temperature coefficient of resistance of a wire is 0.00125 per °C. At 300 K, its resistance is 1Ω. The resistance of the wire will be 2Ω at …………….
(a) 1154 K
(b) 1100 K
(c) 1400K
(d) 1127 K
Answer:
Question 3.
n resistances, each of r Ω, when connected in parallel give an equivalent resistance of R Ω. If these resistances were connected in series, the combination would have a resistance in horns equal to ………..
(a) n2R
(b) \(\frac{R}{n^{2}}\)
(c) \(\frac{R}{n}\)
(d) nR
Answer:
(a) n2R
Hint :
Resistance in parallel combination, R= r/n = r = Rn
Resistance in series combination , R = nr = n2R
![]()
Question 4.
A thin insulated wire forms a plane spiral of N = 100 tight turns carrying a current 1 = 8 m A (milli ampere). The radii of inside and outside turns are a = 50 mm and b = 100 mm respectively. The magnetic induction at the center of the spiral is……………………….
(a) 5 μT
(b) 7 μT
(c) 8 μT
(d) 10 μT
Answer:
(b) 7 μT
Question 5.
In an oscillating LC circuit, the maximum charge on the capacitor is Q. The charge on the capacitor, when the energy is stored equally between the electric and magnetic fields, is……………………….
(a) \(\frac{Q}{2} \)
(b) \(\frac{Q}{\sqrt{3}}\)
(c) \(\frac{Q}{\sqrt{2}}\)
(d) Q
Answer:
(c) \(\frac{Q}{\sqrt{2}}\)
Question 6.
The direction of induced current during electro magnetic induction is given by …………………………………..
(a) Faraday’s law
(b) Lenz’s law
(c) Maxwell’s law
(d) Ampere’s law
Answer:
(b) Lenz’s law
Question 7.
In an electromagnetic wave in free space the rms value of the electric field is 3 V m . The peak value of the magnetic field is………………………..
(a) 1.414 x 10-8 T
(b) 1.0 x 10-8 T
(c) 2.828 x 10-8 T
(d) 2.0 x 10-8 T
Answer:
(a) 1.414 x 10-8 T
![]()
Question 8.
Two point white dots are 1 mm apart on a black paper. They are viewed by eye of pupil diameter 3 mm approximately. The maximum distance at which these dots can be resolved by the eye is, [take wavelength of light, λ = 500 nm]
(a) 1m
(b) 5m
(c) 3m
(d) 6m
Answer:
(b) 5m
Hint:
Resolution limit sin θ =
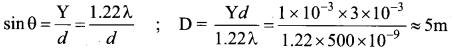
Question 9.
Two mirrors are kept at 60° to each other and a body is placed at middle. The total number of images formed is ……………..
(a) six
(b) four
(c) five
(d) three
Answer:
(a) six
Hint:
Number of images formed \(n=\frac{360}{\theta}-1=\frac{360}{60}-1=5\)
Question 10.
The threshold wavelength for a metal surface whose photoelectric work function is 3.313 eV is
{a) 4125 Å
(b) 3750 Å
(c) 6000 Å
(d) 2062.5 Å
Answer:
(b) 3750 Å
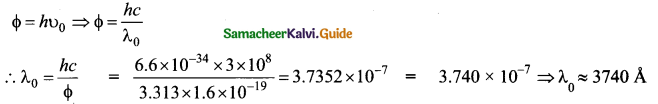
Question 11.
Suppose an alpha particle accelerated by a potential of V volt is allowed to collide with a nucleus whose atomic number is Z, then the distance of closest approach of alpha particle to the nucleus is…..
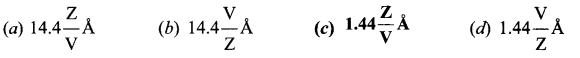
Answer:
(c)
Question 12.
The speed of the particle, that can take discrete values is proportional to ……………
(a) n-3/2
(b) n-3
(c) n1/2
(d) n
Answer:
(d) n
Hint:
\(P=m v=\frac{n h}{2 a} ; V \propto n\)
![]()
Question 13.
Doping semiconductor results in ………………………………
(a) The decrease in mobile charge carriers
(b) The change in chemical properties
(c) The change in the crystal structure
(d) The breaking of the covalent bond
Answer:
(c) The change in the crystal structure
Question 14.
The signal is affected by noise in a communication system …………………….
(a) At the transmitter
(b) At the modulator
(c) In the channel
(d) At the receiver
Answer:
(c) In the channel
Question 15.
The technology used for stopping the brain from processing pain is…………………………..
(a) Precision medicine
(b) Wireless brain sensor
(c) Virtual reality
(d) Radiology
Answer:
(c) Virtual reality
Part – II
Answer any six questions. Question No. 21 is compulsory. [6 x 2 = 12]
Question 16.
Define ‘Electric field’.
Answer:
The electric field at the point P at a distance r from the point charge q is the force experienced by a unit charge and is given by
\(\overrightarrow{\mathrm{E}}=\frac{\overrightarrow{\mathrm{F}}}{q_{0}}\)
The electric field is a vector quantity and its Sl unit is Newton per Coulomb (NC-1).
![]()
Question 17.
State the principle of potentiometer.
Answer:
The basic principle of a potentiometer is that when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length.
Question 18.
Compute the intensity of magnetisation of the bar magnet whose mass, magnetic moment and density are 200 g, 2 A m2 and 8 g cm-3, respectively.
Answer:

Question 19.
What is displacement current?
Answer:
The displacement current can be defined as the current which comes into play in the region in ‘ which the electric field and the electric flux are changing with time.
Question 20.
What is principle of reversibility?
Answer:
The principle of reversibility states that light will follow exactly the same path if its direction of travel is reversed.
![]()
Question 21.
Calculate the de Broglie wavelength of a proton whose kinetic energy is equal to. 81.9 x 1015 (Given: mass of proton is 1836 times that of electron).
Answer:
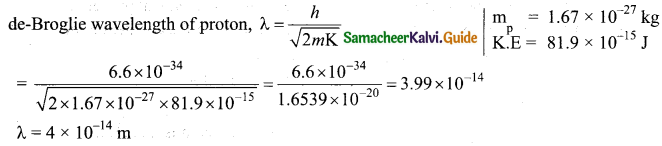
Question 22.
Give the symbolic representation of alpha decay, beta decay and gamma decay.
Answer:
Alpha decay: The alpha decay process symbolically in the following way
Beta decay: β decay is represented by \(_{ z }^{ A }X\rightarrow _{ z,-1 }^{ A }Y+e^{ + }+v\)
Gamma decay: The gamma decay is given \(\mathrm{z} \mathrm{X}^{*} \rightarrow_{Z}^{\mathrm{A}} \mathrm{X} \)+ gamma(y)rays
Question 23.
Explain the need for a feedback circuit in a transistor oscillator.
Answer:
The circuit used to feedback a portion of the output to the input is called the feedback network. If the portion of the output fed to the input is in phase with the input, then the magnitude of the input signal increases. It is necessary for sustained oscillations.
Question 24.
Give the factors that are responsible for transmission impairments.
Answer:
- Attenuation
- Distortion (Harmonic)
- Noise
Part – III
Answer any six questions. Question No. 32 is compulsory. [6 x 3 = 18]
Question 25.
A water molecule has an electric dipole moment of 6.3 x 10 Cm. A sample contains 10 water molecules, with all the dipole moments aligned parallel to the external electric field of magnitude 3 x 10s NC-1. How much work is required to rotate all the water molecules from θ = 0° to 90°?
Answer:
When the water molecules are aligned in the direction of the electric field, it has minimum potential energy. The work done to rotate the dipole from θ = 0° to 90° is equal to the potential energy difference between these two configurations.
W = ΔU = U(90°) – U(0°)
As we know, U = -pE cos θ, Next we calculate the work done to rotate one water molecule
from θ = 0° to 90°,
For one water molecule, W = – pE cos 90° + pE cos 0° = pE
W = 6.3 x10-30 x 3 x 105 = 18.9 x 10-25
For 1022 water molecules, the total work done is Wtot = 18.9x 10 25 x 1022 = 18.9 x 10 3 J
![]()
Question 26.
What are the properties of an equipotential surface?
Answer:
Properties of equipotential surfaces
(i) The work done to move a charge q between any two points A and B,
W = q (VB – VA ). If the points A and B lie on the same equipotential surface, work done is zero because VB – VA
(ii) The electric field is normal to an equipotential surface. If it is not normal, then there is a component of the field parallel to the surface. Then work must be done to move a charge between two points on the same surface. This is a contradiction. Therefore the electric field must always be normal to an equipotential surface.
Question 27.
An electronics hobbyist is building a radio which requires 150 ft in her circuit, but she has only 220 Ω 79 Ω and 92 Ω resistors available. How can she connect the available resistors to get desired value of resistance?
Answer:
Required effective resistance = 150 ft
Given resistors of resistance, R = 220 ft, R = 79 ft, R = 92 ft
Parallel combination of R1 and R2

![]()
Question 28.
What is magnetic permeability?
Answer:
Magnetic permeability: The magnetic permeability can be defined as the measure of ability of the material to allow the passage of magnetic field lines through it or measure of the capacity of the substance to take magnetisation or the degree of penetration of magnetic field through the substance.
Question 29.
A circular metal of area 0.03 m2 rotates in a uniform magnetic field of 0.4 T. The axis of rotation passes through the centre and perpendicular to its plane and is also parallel to the field. If the disc completes 20 revolutions in one second and the resistance of the disc is 4 Ω calculate the induced emf between the axis and the rim and induced current flowing in the disc.
Answer:
A = 0.03 m2; B = 0.4T; f = 20rps; R = 4Ω
Area covered in 1 sec = Area of the disc x frequency
= 0.03 x 20 = 0.6 m2
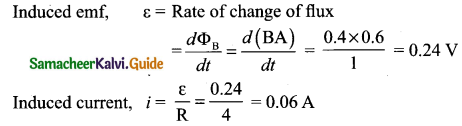
Question 30.
Give the characteristics of image formed by a plane mirror.
Answer:
- The image formed by a plane mirror is virtual, erect, and laterally inverted.
- The size of the image is equal to the size of the object.
- The image distance far behind the mirror is equal to the object distance in front of it.
- If an object is placed between two plane mirrors inclined at an angle 0, then the number of images n formed is as,\(n=\left(\frac{360}{\theta}-1\right)\)
Question 31.
An electron and an alpha particle have same kinetic energy. How are the de Broglie wavelengths associated with them related?
Answer:
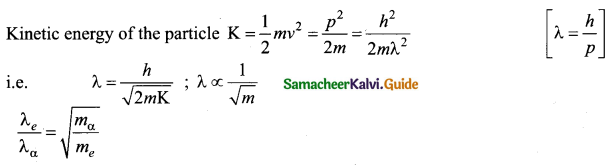
Question 32.
Assuming VCEsat = 0.2 V and β = 50, find the minimum base current (IB) required to drive the transistor given in the figure to saturation.
Answer:
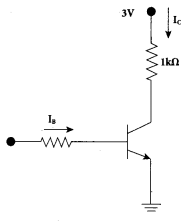
VCEsat = 0.2 V and β = 50
VCE = VCC -IC RC
0.2= 3 – Ic(1 k)

Question 33.
Mention any two advantages and disadvantages of Robotics.
Answer:
(i) Advantages of Robotics:
- The robots are much cheaper than humans.
- Robots never get tired like humans. It can work for 24 x 7. Hence absenteeism in work place can be reduced.
- Robots are more precise and error free in performing the task.
(ii) Disadvantages of Robotics:
- Robots have no sense of emotions or conscience.
- They lack empathy and hence create an emotionless workplace.
- If ultimately robots would do all the work, and the humans will just sit and monitor them* health hazards will increase rapidly.
![]()
Part – IV
Answer all the questions. [5 x 5 = 25]
Question 34.
(a) Derive an expression for electrostatic potential energy of the dipole in a uniform electric field.
Answer:
Expression for electrostatic potential energy of the dipole in a uniform electric field:
Considera dipole placed in the uniform electric field \(\overrightarrow{\mathrm{E}}\) placed in the uniform electric field \(\overrightarrow{\mathrm{E}}\) . A dipole experiences a torque when kept in an uniform electric field E.
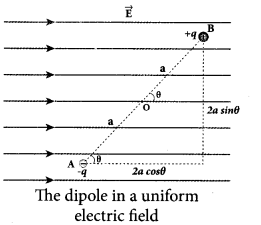
This torque rotates the dipole to align it with the direction of the electric field. To rotate the dipole (at constant angular velocity) from its initial angle θ’ to another angle θ against the torque exerted by the electric field, an equal and opposite external torque must be applied on the dipole. The work done by the external torque to rotate the dipole from angle θ’ to θ at constant angular velocity is
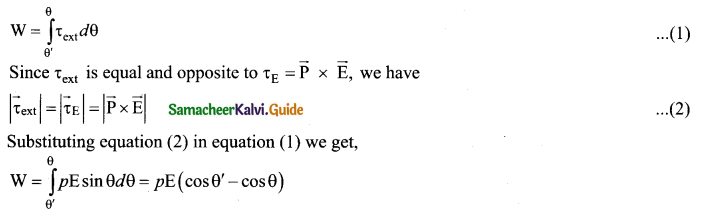
This work done is equal to the potential energy difference between the angular positions 0 and 0′. U(θ) – (Uθ’) = ΔU = -pE cos θ + pE cos θ’.
If the initial angle is = θ’ = 90° and is taken as reference point, then U(θ’) + pE cos 90° = 0. The potential energy stored in the system of dipole kept in the uniform electric field is given by.
U = -pE cos θ = -p-E ……………. (3)
In addition to p and E, the potential energy also depends on the orientation θ of the electric dipole with respect to the external electric field.
The potential energy is maximum when the dipole is aligned anti-parallel (θ = Jt) to the external electric field and minimum when the dipole is aligned parallel (θ = 0) to the external electric field.
[OR]
(b) Deduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current.
Answer:
Magnetic field due to long straight conductor carrying current: Consider a long straight wire NM with current I flowing from N to M. Let P be the point at a distance a from point O.
Consider an element of length dl of the wire at a distance l from point O and \(\vec{r} \) be the vector joining the element dl with the point P. Let θ be the angle between \(d \vec{l} \text { and } \vec{r}\). Then, the magnetic field at P due to the element is
\(d \overrightarrow{\mathrm{B}}=\frac{\mu_{0} \mathrm{Id} l}{4 \pi r^{2}} \sin \theta\)(unit vector perpendicular to \(d \vec{l} \text { and } \vec{r}\)
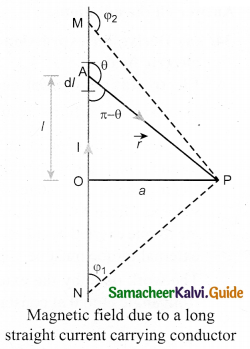
The direction of the field is perpendicular to the plane of the paper and going into it. This can be determined by taking the cross product between two vectors \(d \vec{l} \text { and } \vec{r}\)
(let it be \(\hat{n}\)). The net magnetic field can be determined by integrating equation with proper limits. \(\overrightarrow{\mathrm{B}}=\int d \overrightarrow{\mathrm{B}}\) From the figure, in a right angle triangle PAO,

This is the magnetic field at a point P due to the current in small elemental length. Note that we have expressed the magnetic field OP in terms of angular coordinate i.e. θ. Therefore, the net magnetic field at the point P which can be obtained by integrating \(d \overrightarrow{\mathrm{B}} \) by varying the angle from θ = φ1 to θ =φ2 is
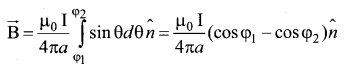
For a an infinitely long straight wire, 1 =0 and 2 =, the magnetic field is \(\overrightarrow{\mathrm{B}}=\frac{\mu_{0} I}{2 \pi a} \hat{n} \) ………… (3)
Note that here \(\hat{n} \) represents the unit vector from the point O to P.
![]()
Question 35.
(a) Obtain an expression for motional emf from Lorentz force.
Answer:
Motional emf from Lorentz force: Consider a straight conducting rod AB of length l in a uniform magnetic field \(\vec{B}\) which is directed perpendicularly into the plane of the paper. The length of the rod is normal to the magnetic field. Let the rod move with a constant velocity \(\vec{v}\) towards right side. When the rod moves, the free electrons present in it also move with same velocity \(\vec{v}\) in B. As a result, the Lorentz force acts on free electrons in the direction from B to A and is given by the relation \(\overrightarrow{\mathrm{F}}_{\mathrm{B}}\)=-
\( e(\vec{v} \times \overrightarrow{\mathrm{B}}) \) …………. (1)
The action of this Lorentz force is to accumulate the free electrons at the end A. This accumulation of free electrons produces a potential difference across the rod which in turn establishes an electric field E directed along BA. Due to the electric field \(\overrightarrow{\mathrm{E}}\), the coulomb force starts acting on the free electrons along AB and is given by
\(\overrightarrow{\mathrm{F}}_{\mathrm{E}}=-e \overrightarrow{\mathrm{E}}\) ……….. (2)
The magnitude of the electric field E keeps on increasing as long as accumulation of electrons at the end A continues. The force \(\overrightarrow{\mathrm{F}}_{\mathrm{B}}\) also increases until equilibrium is reached. At equilibrium, the magnetic Lorentz force \(\overrightarrow{\mathrm{F}}_{\mathrm{B}}\) and the coulomb force F balance each other and no further accumulation of free electrons at the end A takes place,
i.e
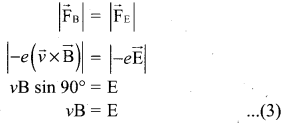
The potential difference between two ends of the rod is
V= El
V= vBl
Thus the Lorentz force on the free electrons is responsible to maintain this potential difference and hence produces an emf
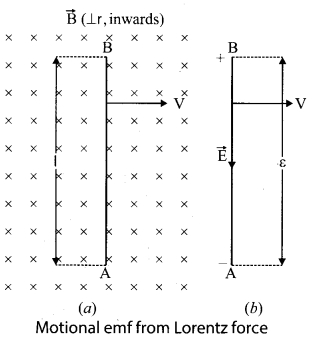
ε = B lv ………….. (4)
As this emf is produced due to the movement of the rod, it is often called as motional emf.
![]()
[OR]
(b) Explain the Maxwell’s modification of Ampere’s circuital law.
Answer:
Maxwell argued that a changing electric field between the capacitor plates must induce a magnetic field. As currents are the usual sources of magnetic fields, a changing electric field must be associated with a current. Maxwell called this current as the displacement current.
If ‘A’ be the area of the capacitor plates and ‘cf be the charge on the plates at any instant ‘f during the charging process, then the electric field in the gap will be
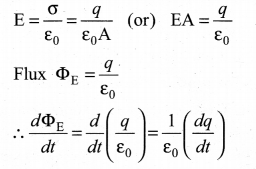
But \(\frac{d q}{d t}\) is the rate of change of charge on the capacitor plates. It is called displacement current and given by \(\mathrm{I}_{d}=\frac{d q}{d t}=\varepsilon_{0} \frac{d \Phi_{\mathrm{E}}}{d t}\)
This is the missing term in Ampere’s Circuital Law. The total current must be the sum of the
conduction current Ic Hence, the modified form of the ampere’s law.
\(\oint_{c} \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_{0}\left(\mathrm{I}_{c}+\varepsilon_{0} \frac{d \Phi_{\mathrm{E}}}{d t}\right)\)
![]()
Question 36.
(a) Obtain the equation for resolving power of microscope.
Answer:
Resolving power of microscope: The diagram related to the calculation of resolution of microscope. A microscope is used to see the details of the object under observation. The ability of microscope depends not only in magnifying the object objective but also in resolving two points on the object separated by a small distance dmin Smaller the value of dmin better will be the resolving power of the microscope.
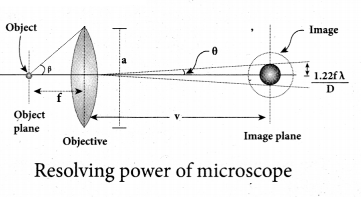
The radius of central maxima is, \(r_{0}=\frac{1.22 \lambda v}{a}\) . In the place of focal length f we have the image distance v. If the difference between the two points on the object to be resolved is dmin, then the magnification m is, \(m=\frac{r_{o}}{d_{\min }}\)
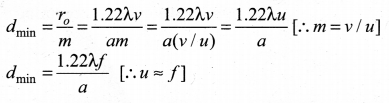
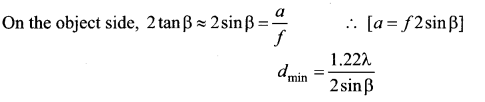
To further reduce the value of dmin the optical path of the light is increased by immersing the objective of the microscope into a bath containing oil of refractive index n.
![]()
Such an objective is called oil immersed objective. The term n sin β is called numerical aperture NA.
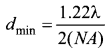
![]()
[OR]
(b) Derive an expression for de Broglie wavelength of electrons.
Answer:
An electron of mass m is accelerated through a potential difference of V volt. The kinetic energy acquired by the electron is given by
\(\frac{1}{2} m v^{2}=e \mathrm{V}\)
Therefore, the speed v of the electron is \(v=\sqrt{\frac{2 e \mathrm{V}}{m}}\)
Hence, the de Broglie wavelength of the electron is \(\lambda=\frac{h}{m v}=\frac{h}{\sqrt{2 e m \mathrm{V}}}\)
Substituting the known values in the above equation, we get
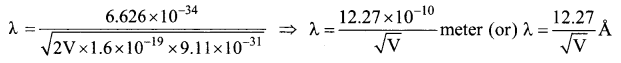
For example, if an electron is accelerated through a potential difference of 100V, then its de Broglie wavelength is 1.227 Å. Since the kinetic energy of the electron, K = eV, then the de Broglie wavelength associated with electron can be also written as
\(\lambda=\frac{h}{\sqrt{2 m \mathrm{K}}}\)
Question 37.
(a) Explain the variation of average binding energy with the mass number by graph and discuss its features.
Answer:
We can find the average binding energy per nucleon \(\overline{\mathrm{BE}}\).
It is given by
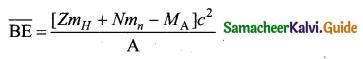
The average binding energy per nucleon is the energy required to separate single nucleon from the particular nucleus. \(\overline{\mathrm{BE}}\) is plotted against A of all known nuclei.
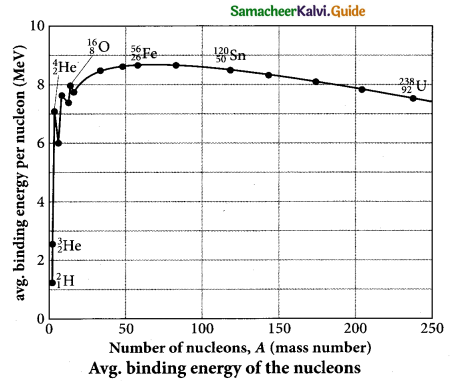
Important inferences from of the average binding energy curve:
- The value of BE rises as the mass number increases until it reaches a maximum value of 8.8 MeV for A= 56 (iron) and then it slowly decreases.
- The average binding energy per nucleon is about 8.5 MeV for nuclei having mass number between A = 40 and 120. These elements are comparatively more stable and not radioactive.
- For higher mass numbers, the curve reduces slowly and BE for uranium is about 7.6 MeV. They are unstable and radioactive. If two light nuclei with A < 28 combine with a nucleus with A < 56, the binding energy per nucleon is more for final nucleus than the initial nuclei. Thus, if the lighter elements combine to produce a nucleus of medium value A, a large amount of energy will be released. This is the basis of nuclear fusion and is the principle of the hydrogen bomb.
- If a nucleus of heavy element is split (fission) into two or more nuclei of medium value A, the energy released would again be large. The atom bomb is based on this principle and huge energy of atom bombs comes from this fission when it is uncontrolled.
![]()
[OR]
(b) State Boolean laws. Elucidate how they are used to simplify Boolean expressions with suitable example.
Answer:
Laws of Boolean Algebra: The NOT, OR and AND operations are \(\bar{A}\), A + B, A.B are the Boolean operations. The results of these operations can be summarised as:
Complement law:
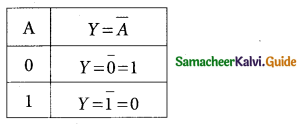
The complement law can be realised as \(\overline{\mathrm{A}}\) = A

Commutative laws
A + B = B +A
A . B = B . A
Associative laws
A + (B + C) = (A + B) + C
A . (B . C) = (A .B) . C
Distributive laws
A( B + C) = AB + AC
A + BC = (A + B) (A + C)
The above laws are used to simplify complicated expressions and to simplify the logic circuitry.
![]()
Question 38.
(a) Modulation helps to reduce the antenna size in wireless communication – Explain. Antenna size:
Answer:
Antenna is used at both transmitter and receiver end. Antenna height is an important parameter to be discussed. The height of the antenna must be a multiple of \(\frac{\lambda}{4}\)
\(h=\frac{\lambda}{4}\) ……………….. (1)
where X is wavelength \(\left(\lambda=\frac{c}{v}\right), c\) c is the velocity of light and v is the frequency of the signal v to be transmitted.
An example
Let us consider two baseband signals. One signal is modulated and the other is not modulated. The frequency of the original baseband signal is taken as v = 10 kHz while the modulated signal is v = 1 MHz. The height of the antenna required to transmit the original baseband signal of frequency
v = 10kHz is

The height of the antenna required to transmit the modulated signal of frequency v = 1 MHz is

Comparing equations (2) and (3), we can infer that it is practically feasible to construct an antenna of height 75 m while the one with 7.5 km is not possible. It clearly manifests that modulated signals reduce the antenna height and are required for long distance transmission.
![]()
[OR]
(b) What are the possible harmful effects of usage of Nanoparticles? Why?
Answer:
Possible harmful effects of usage of Nanoparticles:
The research on the harmful impact of application of nanotechnology is also equally important and fast developing. The major concern here is that the nanoparticles have the dimensions same as that of the biological molecules such as proteins. They may easily get absorbed onto the surface of living organisms and they might enter the tissues and fluids of the body.
The adsorbing nature depends on the surface of the nanoparticle. Indeed, it is possible to deliver a drug directly to a specific cell in the body by designing the surface of a nanoparticle so that it adsorbs specifically onto the surface of the target cell.
The interaction with living systems is also affected by the dimensions of the nanoparticles. For instance, nanoparticles of a few nanometers size may reach well inside biomolecules, which is not possible for larger nanoparticles. Nanoparticles can also cross cell membranes.
It is also possible for the inhaled nanoparticles to reach the blood, to reach other sites such as the liver, heart or blood cells. Researchers are trying to understand the response of living organisms to the presence of nanoparticles of varying size, shape, chemical composition and surface characteristics.