TN State Board 11th Chemistry Important Questions Chapter 6 Gaseous State
Question 1.
Give the characteristics of gases.
Answer:
(i) They assume the volume and shape of their container.
(ii) They are the most compressible state of matter.
(iii) They mix thoroughly when confined to the same container.
(iv) They have much lower densities than liquids and solids.
(v) Their pressure is uniform on all sides of the container.
Question 2.
Mention the units of pressure in SI units.
Answer:
The SI unit of pressure is the Pascal (Pa),
1 Pa = 1 Nm-2 (Newton per second)
1 N = 1 kgms-2 (Kilogram mter per second)
![]()
Question 3.
Define atmospheric pressure.
Answer:
The force exerted on a unit area of earth by the column of air above it is called atmospheric pressure.
Question 4.
Define standard atmospheric pressure.
Answer:
The standard atmospheric pressure (1 atm.) is the pressure that supports a column of mercury exactly 760 mm (or 76 cm) high at 0°C at sea level. The standard atmosphere is thus equal to a pressure of 760 mm Hg, in which mm Hg represents the pressure exerted by a column of mercury 1 mm high.
Thus 1 atm. = 760 mm Hg
![]()
Question 5.
Describe an experiment to verify Boyle’s law.
Answer:
The schematic of the apparatus used
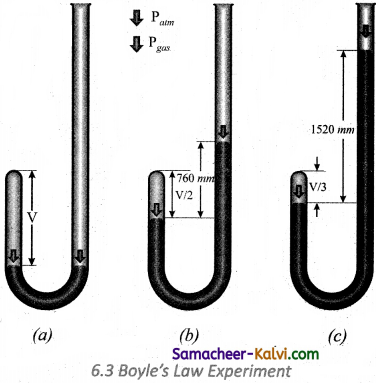
Mercury was added through the open end of the apparatus such that the mercury level on both ends are equal as shown in the figure
(a) Add more amount of mercury until the volume of the trapped air is reduced to half of its original volume as shown in figure
(b) The pressure exerted on the gas by the addition of excess mercury is given by the difference in mercury levels of the tube. Initially the pressure exerted by the gas is equal to 1 atm as the difference in height of the mercury levels is zero.
When the volume is reduced to half, the difference in mercury levels increases to 760 mm. Now the pressure exerted by the gas is equal to 2 atm. It led him to conclude that at a given temperature the volume occupied by a fixed mass of a gas is inversely proportional to its pressure.
Mathematically, the Boyle’s law can be written as
V ∝ \(\frac{1}{\mathrm{P}}\) …………..(1)
(T and n are fixed, T-temperature, n- number of moles)
V = k × \(\frac{1}{\mathrm{P}}\) …………(2)
k – proportionality constant When we rearrange equation (2).
PV = k at constant temperature and mass.
![]()
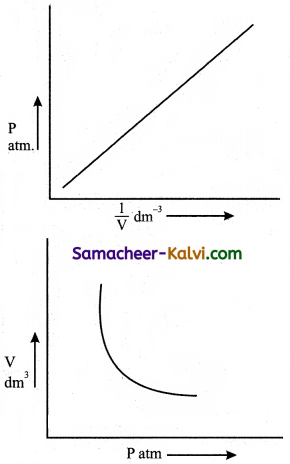
Question 6.
Give the graphical representation of Boyle’s law.
Answer:
According to Boyle’s law for a given mass of a gas under two different sets of conditions at constant temperature we can write
P1V1 = P2V2 = k
Question 7.
Prove that density of a gas in directly proportional to the pressure.
[OR] Derive pressure-density relationship from Boyle’s law.
Answer:
The pressure-density relationship can be derived from the Boyle’s law as shown below.
P1V1 = P2V2 (Boyle’s law)
P1 \(\frac{m}{d_{1}}\) = P2 \(\frac{m}{d_{2}}\)
Where “m” is the mass, d1 and d2 are the densities of gases at pressure P1 and P2.
\(\frac{P_{1}}{d_{1}}=\frac{P_{2}}{d_{2}}\)In other words, the density of a gas is directly proportional to pressure.
![]()
Question 8.
Explain what happens of a balloon is moved from an ice-cold water bath to a. boiling water bath..
Answer:
If a balloon is moved from an ice cold water bath to a boiling water bath, the temperature of the gas increases. As a result, the gas molecules inside the balloon move faster and gas expands. Hence, the volume increases.
Question 9.
Explain the variation of volume of a gas with temperature at constant pressure.
Answer:
The plot of the volume of the gas against its temperature at a given pressure is shown in the figure.
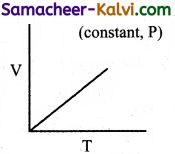
From the graph, it is clear that the volume of the gas linearly increases with temperature at a given pressure. Such lines are called isobars. It can be expressed by the following straight line equation.
V = mT + C where T is the temperature in degree Celsius and m & C are constants.
When T = 0°C the volume becomes V0.
Hence, V0 = C and slope of the straight line m is equal to ∆V / ∆T.
Therefore the above equation can be written in the following form.
V = \(\left(\frac{\Delta V}{\Delta T}\right)\) T + V0 ……………(1)
(n, p are constant)
Divide the equation (1) by V0
\(\frac{\mathrm{V}}{\mathrm{V}_{0}}=\frac{1}{\mathrm{~V}_{0}}\left(\frac{\Delta \mathrm{V}}{\Delta \mathrm{T}}\right)\)T + 1 …………(2)
Charles and Gay Lussac found that under constant pressure, the relative increase in volume per degree increase in temperature is same for all gases. The relative increase in volume per °C (∝) is equal to \(\frac{1}{V_{0}}\left(\frac{\Delta V}{\Delta T}\right)\).
Therefore
V = \(\left(\frac{\Delta V}{\Delta T}\right)\) T + V0
V = V0 (T + 1) …………(3)
Charles found that the coefficient of expansion – is approximately equal to 1/273. It means that at constant temperature for a given mass, for each degree rise in temperature, all gases expand by 1/273 of their volume at 0°C. For refer Figure No. 61.
![]()
Question 10.
Explain why the pressure inprease two fold, when the volume is halved?
Answer:
The pressure is a result of the force of the gas particles on the walls of the container. If the volume is halved, the density is doubled. Hence, twice the number of the particles should be hitting the container and the pressure would be increased to two fold.
Question 11.
Explain why airplanes cabins’are pressurized.
Answer:
The pressure decreases with the increase in altitude because there are fewer molecules per unit volume of air. Above 9200 m (30000 ft.) for example, where most commercial air planes fly, the pressure is so low that one could pass out for lack of oxygen. For this reason most airplanes cabins are artificially pressurized.
Question 12.
How does the volume of a gas vary with temperature at constant pressure? Explain with the help of a plot between volume Vs temperature.
Answer:
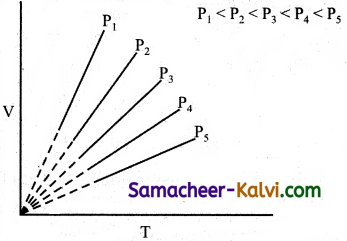
The volume of a gas increases with temperature at constant pressure. Each line (isobar) represents the variation of volume with temperature at certain pressure. The pressure increases from P1 to P.
i.e., P1 < P2 < P3 < P4 < P5.
When these lines are extrapolated of extended to zero volume, they intersect at a temperature of- 273.15°C. All the gases are becoming liquids if they are cooled to sufficiently low temperatures. In other words, all gases occupy zero volume at absolute zero.
![]()
Question 13.
What is absolute zero? Mention its significance.
Answer:
Absolute zero is a temperature at which all gases have zero volume. This temperature cannot be obtained. It has a value of -273.15°C and theoretically it is the lowest temperature obtainable.
Question 14.
What are isobar and isochores?
Answer:
Isobars are the plot of volume Vs temperature at constant pressure and isochores are plot of pressure verses temperature at constant volume.
Question 15.
State Gay Lussac’s law.
Answer:
At constant volume the pressure of a fixed mass of a gas is directly proportional to temperature.
P ∝ T
or \(\frac{\mathrm{P}}{\mathrm{T}}\) = Constant k
If P1 and P2 are the pressures at temperatures T1 and T2, respectively, then from Gay Lussac’s law
![]()
Question 16.
State Avogadro’s hypothesis.
Answer:
Equal volumes of all gases under the same conditions of temperature and pressure contain equal number of molecules. The mathematical form of Avogadro’s hypothesis may be expressed as
V ∝ n
\(\frac{\mathrm{V}_{1}}{n_{1}}=\frac{\mathrm{V}_{2}}{n_{2}}\) = constant
Where V1 and n1 are the volume and number of moles of a gas and V2 and n2 are a different set of values of volume and number of moles of the same gas at same temperature and pressure.
Question 17.
Describe ideal gas equation.
Answer:
The gaseous state is described completely using the following four variables T, P, V and n. Each gas law, relates one variable of a gaseous sample to another while the other two variables are held constant. Therefore, combining all equations into a single equation will enable to account for the change in any or all of the variables.
Derivation of ideal gas equation from empirical gas laws:
Boyle’s law V ∝ \(\frac{1}{\mathrm{P}}\)
Charles law V ∝ T
Avogadro’s law V ∝ n
We can combine these equations into the following general equation that describes the physical behaviour of all gases.
V ∝ \(\frac{n \mathrm{~T}}{\mathrm{P}}\)
V = \(\frac{n \mathrm{RT}}{\mathrm{P}}\)
where, R is the proportionality constant. The above equation can be rearranged to give
PV = nRT
![]()
Question 18.
Arrive at the values of gas constant (R) in dm3 atm mol-1 K-1, Pa, m3 K-1, mol-1 at JK-1 mol-1.
Answer:
The numerical value; of the gas constant (R) can be calculated by using the equation
R = \(\frac{\mathrm{PV}}{n \mathrm{~T}}\) (R is also known as the universal gas constant) ,
For standard conditions in which P is 1 atm,, volume 22.414 dm3, for 1 mole at 273.15 (~ 273) K. .
R = \(\frac{1 \mathrm{~atm} . \times 22.414 \mathrm{dm}^{3}}{1 \mathrm{~mol} \times 273.15 \mathrm{~K}}\)
= 0.0821 dm3 atm . mole-1 K-1
Where P = 105 pascal, V = 22.71 × 10-3 m3 for 1 mole of a gas at 273.15 K
R = \(\frac{10^{5} \mathrm{~Pa} \times 22.71 \times 10^{-3} \mathrm{~m}^{3}}{1 \mathrm{~mol} \times 273.15 \mathrm{~K}}\)
= 8.314 Pa m3 K-1 mol-1
= 8.314 × 10-2 bar dm3 K-1 mol-1
= 8.314 JK-1 mol-1
Question 19.
What is partial pressure of a gas?
Answer:
Partial pressure of a gas is the pressure exerted by the gas when it is present alone in that volume. This term is used to indicate the pressure of a gaseous component in a mixture of gases.
![]()
Question 20.
State Dalton’s law of partial pressure.
Answer:
The total pressure of a mixture of non-reacting gases is the sum of partial pressures of the gases present. Partial pressure of a gas is the pressure exerted by the gas when it is present alone occupies to entire volume of the vessel.
Question 21.
Express mathematically Dalton’s law of partial pressures.
Answer:
Let for gases 1, 2 and 3 the partial pressure are P1, P2 and P3
Mathematically,
PTotal = P1 + P2 + P3
when we consider the gases to behave ideally
P1 = n1 \(\frac{\mathrm{RT}}{\mathrm{V}}\);
P2 = n2 \(\frac{\mathrm{RT}}{\mathrm{V}}\);
P3 = n3 \(\frac{\mathrm{RT}}{\mathrm{V}}\);
PTotal = n1 \(\frac{\mathrm{RT}}{\mathrm{V}}\) + n2 \(\frac{\mathrm{RT}}{\mathrm{V}}\) + n3 \(\frac{\mathrm{RT}}{\mathrm{V}}\)
= (n1 + n2 + n3) \(\frac{\mathrm{RT}}{\mathrm{V}}\)
P1 = nTotal (\(\frac{\mathrm{RT}}{\mathrm{V}}\))
The partial pressure can be expressed as mole fraction multiplied Xi by the total pressure.
Pi = Xi PTotal
Xi = \(\frac{n_{i}}{\sum n_{i}}\)
= (number of mol of the gas 1) / (Total number of mol of all gases)
![]()
Question 22.
Mention the application of Dalton’s law.
Answer:
In a reaction involving the collection of gas by downward displacement of water, the pressure of dry vapour collected can be calculated using Dalton’s law.
Pdry gas collected = PTotal – Pwater vapour
Pwater vapour is generally referred as aqueous tension and its values are available for air at various temperatures. These values are relevant in weather forecast.
Question 23.
State Graham’s law of diffusion.
Answer:
The rate of effusion or diffusion of a gas is inversely proportional to the square root of molar mass at constant temperature and pressure.
Question 24.
Define rate of diffusion.
Answer:
It is defined as the number of molecules of a gas that get diffused in unit time.
Rate of diffusion = \(\frac{\text { Volume of the gas diffused }}{\text { time taken }}\)
![]()
Question 25.
Give an expression for the rate of diffusion of a gas and to its molecular weight.
Answer:
Rate of diffusion ∝ \(\frac{1}{\sqrt{M}}\)
Question 26.
Give an expression for the rates of diffusion of two different gases and their molecular weighs.
Answer:
\(\frac{r_{\mathrm{A}}}{r_{\mathrm{B}}}=\sqrt{\frac{\mathrm{M}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{A}}}}\)
rA and rB rates of diffusion of gases A and B and the MA and MB are their molecular weighs.
Question 27.
Give an expression for»the diffusion of two gases diffusing at different pressures PA and PB and their molecular weighs.
Answer:
When diffusing gases are at different pressures (PA, PB)
Where rA and rB are the rates of diffusion of A and B and the MA and MB are their respective molecular masses.
![]()
Question 28.
Mention the postulates of kinetic theory of gases which do not explain the behaviour of real gases.
Answer:
The assumption that molecules in the gas phase occupy negligible volume (1) and that they do not exert any force oh one another either attractive or repulsive (2) do not account for the behaviour of real gas.
Question 29.
What are the observations that you get from the plot of Z Vs P. (PV / RT Vs P) for real gases?
Answer:
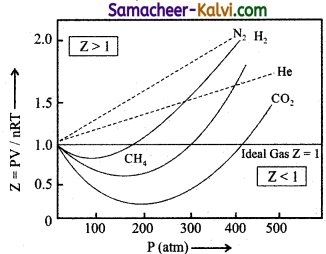
(i) For 1 mole of an ideal the plot becomes parallel to the pressure axis.
(ii) At low pressures all gases exhibit ideal behaviour. \(\frac{\mathrm{PV}}{\mathrm{RT}}\) values converges to 1 as P approaches to zero.
(iii) At moderate pressures, \(\frac{\mathrm{PV}}{\mathrm{RT}}\) becomes less than 1. This means that gases exhibit negative deviation from ideal behaviour. This is because attractive forces operate among molecules at relatively short distances.
(iv) At high pressures, \(\frac{\mathrm{PV}}{\mathrm{RT}}\) becomes greater than 1. This means that gases exhibit negative deviation from ideal behaviour. Intermolecular force becomes significant effect to affect the motion of the molecules.
![]()
Question 30.
Explain why in the case of a real gas the measured pressure is lower than the pressure of the gas if it behaved ideally.
Answer:
The speed of a’molecule that is moving toward the wall of a container is reduced by the attractive forces exerted by its neighbouring molecules. Hence, the measured gas pressure is lower than the pressure the gas would exert, if it behaved ideally.
Question 31.
What is compressibility factor? How does it explain the deviation of non-ideal gases from ideal behaviour.
Answer:
Compressibility factor is the ratio of PV to nRT.
Z = \(\frac{\mathrm{PV}}{n \mathrm{RT}}\)
For ideal gases PV = nRT i.e., Z = 1
At high pressures Z > 1 (Positive deviation)
At intermediate pressures Z < 1 (Negative deviation) Question 32. Explain the term ‘Boyle’s point’. Mention it significance. Answer: (i) Boyle’s point is the temperature at which, real gases behave ideally over a range of low pressures. (ii) The Boyle point varies with the nature of the gas. (iii) Above the Boyle point, Z > 1 for real gases, i.e., they show positive deviation.
(iv) Below the Boyle point, the real gases first show a decrease for Z, reaches a minimum and then increase with increase in pressure.
![]()
Question 33.
Under what conditions, do real gases behave ideally?
Answer:
The real gases behave ideally at low pressure and at high temperature.
Question 34.
Show how the molar volume.of a real and . ideal gas are related to each other?
Answer:
Z = \(\frac{\mathrm{PV}_{\text {real }}}{n \mathrm{RT}}\) ………..(1)
Videal = \(\frac{n \mathrm{RT}}{\mathrm{P}}\) …………..(2)
Substituting (2) in (1)
Z = \(\frac{\mathbf{V}_{\text {real }}}{\mathbf{V}_{\text {ideal }}}\)
Where Vreal is the molar volume of the real gas and ideal is the molar volume of it when it behaves ideal, i.e., compressibility is the ratio of real volume of the gas to ideal volume of any gas.
Question 35.
Explain Andrew’s isotherm of carbon dioxide.
Answer:
The isotherms of carbon dioxide at different temperatures is shown in figure.
From the plots we can infer the following:
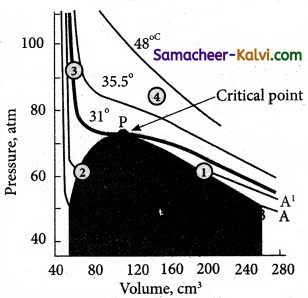
At 13° C, carbondioxides exists as a gas at point A. Increasing the pressure of the gas decreases its volume to the point B. The volume of carbondioxide remains constant, till the point C. At the point B, carbon dioxide gets converted to liquid carbondioxide.
Along the line BC, carbondioxide exists both as vapour and liquid. They are in equilibrium with each other. At point ‘C’, carbondioxide is completely converted to liquid. Further increase of pressure at point ‘C’ has very little effect on the volume of carbondioxide. This is reflected in the steep rise in the curve.
Increasing the temperature, decreases the portion of the straight line (BC), which represents the co-existence of liquid and gaseous carbondioxide. At temperature 31°C the portion of the straight line becomes a point ‘P’. At their point, the entire gaseous carbondioxide is converted into liquid. This temperature, is known as critical temperature.
Above this temperature, carbondioxide exists as a gas and cannot be liquefied whatever be the pressure. Below this temperature, carbon dioxide can be readily converted to liquid by the application of pressure.
![]()
Question 36.
Using Andrew’s isotherm of CO2 explain the terms
(i) critical temperature,
(ii) critical pressure and
(iii) critical volume.
Answer:
(i) At the temperature of 31°C CO2 remains as a gas and below this temperature, CO2 can be converted to a liquid. Thus, this . temperature is called critical temperature. Above this temperature, CO2 exists mainly as a gas.
(ii) The pressure required to liquefy a gas at its critical temperature is known as critical pressure. For CO2, it is 73 atm.
(iii) The volume occupied by one mol of CO2 at its critical temperature and critical pressure is known as critical volume.
Question 37.
Explain Joule Thomson effect.
Answer:
The phenomenon of lowering of temperature when a gas is made to expand adiabatically from a region of high pressure into a region of low pressure is known as Joule – Thomson effect.
![]()
Question 38.
Which of the gases can be liquefied by Joule Thomson effect?
Answer:
Gases like O2, He, N2 and H2 have very low Tc, hence Joule-Thomson effect can be applied for cooling effectively for liquefaction.
Question 39.
What is inversion temperature? How is it related to Vander Waals constants?
Answer:
The temperature below which a gas obey Joule Thomson effect is called inversion temperature (Ti). At the inversion temperature, no rise or fall intemperature of a gas occurs while expanding. But above the inversion temperature, the gas gets heated up when allowed to expand through a hole. It is related to Vander Waals equation by
T2 = \(\frac{2 a}{R b}\)
Question 40.
Mention different methods of liquefaction of gases.There are different methods used for liquefaction of gases.
Answer:
(i) In Linde’s method: Joule-Thomson effect is used to get liquid air or any other gas.
(ii) Claude’s process: In addition to Joule- Thomson effect, the gas is allowed to perform mechanical work. So that more cooling is produced.
(iii) Adiabatic process: This method of cooling is produced by removing the magnetic property of magnetic material such as gadolinium sulphate. By this method, a temperature of 10-4 K i.e., as low as zero Kelvin can be achieved.
![]()
Question 41.
Inside a certain automobile engine, the volume of air in a cylinder is 0.475 dm3, when the pressure is 1.05 atm. When the gas is compressed, the pressure increased to 5.65 atm. at the same temperature. What is the volume of compressed air?
Answer:
Volume of air in the cylinder V1 = 0.475 dm3
Pressure of air (P1) = 1.05 atm
Pressure after compression of the gas (P2) = 5.65 atm
Volume of air after (V2) compression = ?
P1V1 = P2V2
1.05 × 0.475 = 5.65 × V2
V2 = \(\frac{1.05 \times 0.475}{5 .65}\) dm3 = 0.088 dm3
Question 42.
An inflated balloon has a volume of 275 mL and contains 0.120 mole of air. As shown in fig a piece of dry ice weighing lg is placed in the balloon and its neck is tied. What is the volume of the balloon after dry ice (solid CO2) has vapourized? Assume pressure and temperature to remain constant.
Answer:
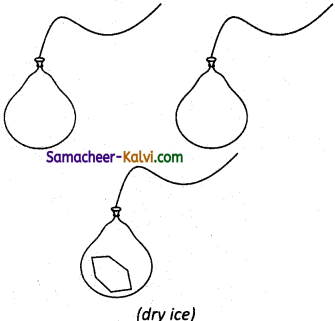
(Avogadro’s hypothesis: The addition of carbondioxide to the balloon increases the number of molecules, which increases the volume).
Volume of the inflated balloon (V1) = 275 mL
Number of mole of air (n1) = 0.120 mol
No. of mol of CO2 introduced = \(\frac{1}{44}\) = 0.023
Total no. of mol of air + CO2 = 0.120 + 0.023 = 0.143 mol
Final volume of the balloon after CO2has vaporised = \(\frac{\mathrm{V}_{1}}{n_{1}}=\frac{\mathrm{V}_{2}}{n_{2}}\) or
V2 = \(\frac{273 \times 0.143}{0.120}\) = 325.325 mL
![]()
Question 43.
A sample of solid KClO3 (potassium chlorate) was heated in a test tube to obtain O2 according to the reaction 2KClO3 —» 2KCl + 3O2. The oxygen gas was collected by downward displacement of water at 295 K. The total pressure of the mixture is 772 mm of Hg and the vapour pressure of water is 26.7 mm of Hg at 300K. What is the partial pressure of the oxygen gas?
Answer:
Total pressure of mixture of O2 and H2O vapour = 772 mm of Hg
Vapour pressure of H2O = 26.7 mm of Hg
Pressure of O2 gas = 754.3 mm of Hg
Question 44.
Find the ratio of effusion rates of hydrogen and krypton gas.
Answer:
Molecular mass of H2 = 2 g mol-1
Molecular mass of Kr = 83g mol-1
\(\frac{r_{\mathrm{H}_{2}}}{r_{\mathrm{Kr}}}=\sqrt{\frac{\mathrm{M}_{\mathrm{kr}}}{\mathrm{M}_{\mathrm{H}_{2}}}}\)
= \(\sqrt{\frac{83}{2}}=\sqrt{41.5}\)
\(\sqrt{\frac{83}{2}}=\sqrt{41.5}\) = 6.44
![]()
Question 45.
If the weather balloon at a.pressure 0.0965 atm. at ground level has a volume of 10.0 m3. What will be the pressure at an altitude of 5300 m where its volume is 20.0 m3?
Answer:
Given:
P1 = 0.0965 atm; V1 = 10.0 m3 or 10 × 103 mL
P2 = ?
V2 = 20.0 m3 or 20 × 103 mL
using P1V1 = P2V2
= 0.0965 × 10 × 103
= P2 × 20 × 103
P2 = \(\frac{0.0965 \times 10}{20}\) = 0.04825 atm
Question 46.
At sea level a balloon has volume of 785 x 10-3 dm3. What will be its volume, if it taken to a place where the pressure is 0052 atm less than the atmospheric pressure of 1 atm.
Answer:
Pressure of the gas (P1) = 1 atm
Volume of the gas (V1) = 785 x 10-3 dm3
Pressure of the gas (P2) = 1 atm – 0.0052 atm , = 0.9948 atm
Volume of the gas (V2) = ?
P1V1= P2V2
1 × 785 × 10-3 = 0.9948 × V2
V2 = \(\frac{1 \times 785 \times 10^{-3}}{0.9948}\) = 789 × 10-3
![]()
Question 47.
When the temperature of a gas increases from 0°C the volume of the gas increases by a factor of 1.25. what is the final temperature?
Answer:
Temperature (T1) = 0°C = 273 K
Volume of the gas = V1 cm3
Temperature (T2) = ?
Volume of the gas (V2) = 1.25 V1

Question 48.
A helium filled balloon had a volume of 400 mL, when it is cooled to – 120°C. What will be its volume if the balloon is warmed in an oven to 100° C assuming no changes in pressure.
Answer:
Initial volume (V1) = 400 mL
Initial temperature (T1) = 273 – 120 = 153 K
Final volume (V2) = ?
Final temperature (T2) = 100 + 273 = 373 K
\(\frac{400}{153}=\frac{V_{2}}{373}\) (or)
V2 = \(\frac{400 \times 373}{153}\) = 975.2 mL
![]()
Question 49.
A steel tank contains carbondioxide at 300 K and a pressure of 10 atm. Calculate the internal gas pressure when the tank gas is heated to 373 K.
Answer:
Given, P1 = 10 atm; P2 = ?; T1 = 300K; T2 = 373
\(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)
P2 = T2 = 373
\(\frac{100}{300}=\frac{P_{2}}{373}\) = 124.3 atm
Question 50.
In an experiment of verification of Charle’s law, the following are the set of readings taken by a student.
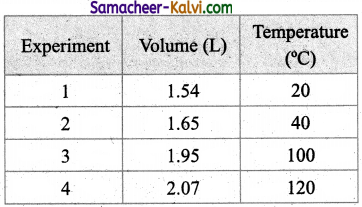
What is the average value of the constant of proportionality?
Answer:
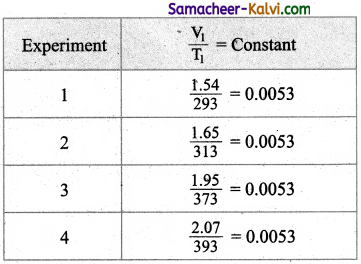
The average value of the constant is 0.0053.
![]()
Question 51.
Pressure of 1 g of an ideal gas at 27°C is found to be 2 bar. When 2 g of another ideal gas B is -introduced in the same flash at ike same temperature, the pressure becomes 3 bar. Find the relationship between their molar masses.
Answer:
Let the molar masses of gases A and B are MA and MB respectively. Then their number of moles will be,
nA = \(\frac{1}{\mathrm{M}_{\mathrm{A}}}\);
nB = \(\frac{2}{\mathrm{M}_{\mathrm{B}}}\)
PA = 2 bar;
PA + PB = 3 bar
i.e., PB = 1 bar
Applying equation,
PV = nRT
PAV = nART;
PBV = nBRT

Question 52.
Density of a gas is formed to be 5.46g/dm3 at 27°C and at 2 bar pressure. What will be its density at STP?
Answer:
Density (d) = \(\frac{\mathrm{MP}}{\mathrm{RT}}\)
Where M is the molar mass, P and T are the temperature and pressure of the gas respectively.
Given:
d1 = 5.46g/dm3; T1 = 27°C = 300K;
P1 = 2 bar; d2 = ?
T2 = 0°C = 273K; P2 = 1 bar.
Using the above equation
d2 = 3 g/dm3.
![]()
Question 53.
Calculate the total pressure in a mixture of 8 g of oxygen and 4 g of hydrogen confined in a vessel of 1 dm3 at 27° C. [R = 0.083 bar dm3 K-1 mol-1.]
Answer:
Molar mass of O2 = 32 g mol-1
∴ 8g of O2 = \(\frac{8}{32}\) mol = 0.25 mol
Molar mass of H2 = 2 g mol-1
∴ 4 g of H2 = \(\frac{4}{42}\) mol = 2 mol
Total number of mol (n) = 0.25 + 2 = 2.25
Given:
Volume (V) = 1 dm3;
Temperature (T) = 27° C = 300 K
R = 0.083 bar dm3 K-1 mol-1
PV = nRT (or)
P = \(\frac{n \mathrm{RT}}{\mathrm{V}}\)

P = 56.025 bar
Question 54.
20 cm3 of SO2 diffuse through a pores partition in 60s. What volume of O2 will diffuse under similar conditions in 30s?
Answer:
Rate of diffusion of (rSO2) = \(\frac{20 \mathrm{dm}^{3}}{60 \mathrm{~s}}=\frac{1}{3}\) dm3s-1
Rate of diffusion of (rO2) = \(\frac{\mathrm{V}}{30}\) dm3s-1
Applying Graham’s law
\(\frac{\mathrm{V} / 30}{1 / 3}=\sqrt{\frac{64}{32}}\)
\(\frac{\mathrm{V}}{10}\) = √2 = 1.414
1.414 × 10 = 14.14 dm3.
![]()
Question 55.
8 g of methane is placed in a 5 litre container at 27° C. Find Boyle’s constant.
Answer:
PV = Boyle’s constant.
But PV = nRT = \(\frac{w}{M}\) × RT
= \(\frac{8}{10}\) mol × 0.0821 L atm K-1mol-1 × 300K = 12.315 Latm.
Hence Boyle’s constant is 12.315 L atm.
Question 56.
A neon-di-oxygen mixture contains 70.6 g of di-oxygen and 167.5 g of neon. If the pressure of the mixture of gases in the cylinder is 25 bar, what is the partial pressure of di-oxygen and neon in the mixture? (Atomic mass of Ne = 20u)
Answer:
No. of mol of dioxygen (n)O2 = \(\frac{\text { mass of } \mathrm{O}_{2}}{\text { molar mass of } \mathrm{O}_{2}}\)
= \(\frac{70.6 \mathrm{~g}}{32.0 \mathrm{gmol}^{-1}}\) = 2.21 mol
No. of mol of neon (nNe) = \(\frac{\text { mass of } \mathrm{Ne}}{\text { molar mass of } \mathrm{Ne}}=\frac{167.5 \mathrm{~g}}{20 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 8.375 mol.
mole fraction of di-hydrogen = \(\frac{n_{\mathrm{O}_{2}}}{n_{\mathrm{O}_{2}}+n_{\mathrm{Ne}}}=\frac{2.21}{2.21+8.375}\)
mole fraction of neon = 1 – 0.21 = 0.79
partial pressure of O2 = mole fraction of O2 × Total pressure
= 0.21 × 25 bar = 5.25 bar
partial pressure of Ne = mole fraction of Ne × Total pressure = 0.79 × 25 bar = 19.75 bar
![]()
Question 57.
One mol of SO2 gas occupies a volume of 500 mL. at 27°C and 50 atm pressure. Calculate the compressibility factor of the gas. Comment on the type of deviation shown by the gas from the ideal behaviour.
Answer:
Compressibility factor (Z) = \(\frac{\mathrm{PV}}{n \mathrm{RT}}\)
Given: n = 1; P = 50 atm;
V = 350 × 10-3 L = 0.35 L
R = 0.0821 L atm K-1 mol-1
T = 27 + 273 = 300 K
Substituting these values in the above equation
Z = \(\frac{(50 \mathrm{~atm})(0.35 \mathrm{~L})}{1 \mathrm{~mol}\left(0.821 \mathrm{~L} \mathrm{~atm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)(300 \mathrm{~K})}\) = 0.711
Since, Z < 1, the gas shows negative deviation frofn ideal behaviour.
Question 58.
The Vander Waal’s constant ‘b’ for oxygen is 0.0318 L mol-1 . Calculate the diameter, of the oxygen molecule.
Answer:
b = 4V (or)
V = \(\frac{b}{4}=\frac{0.0318}{4}\) = 7.95 × 10-3 L mol-1
= 7.95 cm3 mol-1
Volume occupied by one mole of O2 molecule = \(\frac{7.95}{6.02 \times 10^{23}}\)
= 1.32 × 10-23cm3
Considering the molecule to be spherical,
V = \(\frac{4}{3}\) πr3 = 1.32 × 10“23 cm3
r3 = 3.15 × 10-24
Solving r = 1.466 × 10-8 cm
Diameter 2r = 2 × 1.466 × 10-8 cm
= 2.932 × 10-8 cm = 2.932 Å
![]()
Question 59.
An LPG cylinder containing 15 kg of butane at 27° C and 10 atm pressure is leaking. After one day,.its pressure is decreased to 8 atm. How much quality of the gas is leaked?
Answer:
PV = nRT. Here T and V are constant.
Hence \(\frac{\mathrm{P}_{1}}{\mathrm{P}_{2}}=\frac{n_{1}}{n_{2}}=\frac{w_{1}}{w_{2}}\)
Where Pj and P2 are the initial and final pressures.
i.e., P1 = 10 atm; P2 = 8 atm.
w1 and w2 weight of the gas present initiates and after leaking,
w1 = 15 kg : w2 = ?
∴ \(\frac{10}{8}=\frac{15}{w_{2}}\) (or)
w2 = 12 kg
Hence, the amount of gas leaked is .15 – 12 = 3 kg.
Question 60.
A balloon filled with air at room temperature and cooled to a much lower temperature can be used as a model for Charle’s law.
Answer:
The volume of air decreases as the temperature is lowered, i.e., its density increases. Thus a cooled air is heavier than atmospheric air. (The reverse fact is in made use of in filling hot air in the balloon which use up for meterological observations).
![]()
Question 61.
When the driver of an automobile applies brake, the passengers are pushed toward the front of the car but a helium balloon is pushed toward back of the car. Upon forward acceleration the passengers are pushed toward the front of the car. Why?
Answer:
When the car is accelerated forward, the air inside moves back relative to the car. This creates a slightly high pressure in the rear of the vehicle and a low pressure up front. Hence . the passengers are pushed towards the front of the car. This relative pressure difference in front and near of the car is responsible for pushing the passengers towards the front of the car. Since helium is lighter than air, it moves away from the region of high pressures.
![]()
Choose the correct answer:
Question 1.
The scope of the plot between PV and P at constant temperature is:
(a) zero
(b) 1
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(a) zero
Hint:
It is a straight line. Hence the slope is zero.
Question 2.
Which of the following diagram directly describes the behaviour of a fixed mass of an ideal gas?
(a) 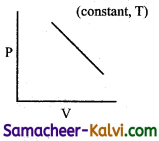
(b) 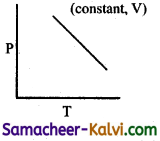
(c) 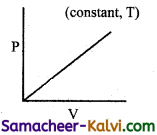
(d) 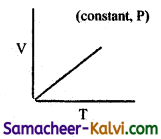
Answer:
(d) 
Hint:
At constant pressure, \(\frac{\mathrm{V}}{\mathrm{T}}\) = constant or V = KT. plot of V Vs T will be linear passing through origin.
![]()
Question 3.
The density of neon will be highest at:
(a) STP
(b) 0°C, 2 atm
(c) 273°C, 1 atm
(d) 273°C, 2 atm
Answer:
(b) 0°C, 2 atm
Hint:
d = \(\frac{\text { PM }}{\text { RT }}\) or
d ∝ \(\frac{\mathrm{P}}{\mathrm{T}}\)
Question 4.
Gas equation PV = nRT is obeyed by:
(a) only isothermal process
(b) only adiabatic process
(c) both (a) and (b)
(d) none of the above
Answer:
(c) both (a) and (b)
Question 5.
Molar volume of CO2 is maximum at:
(a) NTP
(b) 0°C and 2.0 atm
(c) 127°C and 1 atm
(d) 273°C and 2 atm
Answer:
(c) 127°C and 1 atm
Hint:
PV = RT; V = \(\frac{\mathrm{RT}}{\mathrm{P}}\)
![]()
Question 6.
The density of gas A is twice that of B. Molecular mass of A is half the molecular mass of B. The ratio of the partial pressures of A and B is:
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{4}{1}\)
(d) \(\frac{2}{1}\)
Answer:
(c) \(\frac{4}{1}\)
Hint:
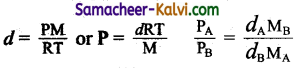
Question 7.
According to Graham’s law at a given temperature, the ratio of rates of diffusion, rA / rB of gases A and B is given by: where P and M are the pressure and molecular mass of gases A and B.
(a) \(\left(\frac{P_{A}}{P_{B}}\right)\left(\frac{M_{A}}{M_{B}}\right)^{\frac{1}{2}}\)
(b) \(\left(\frac{\mathbf{M}_{\mathrm{A}}}{\mathrm{M}_{\mathrm{B}}}\right)\left(\frac{\mathrm{P}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{B}}}\right)^{\frac{1}{2}}\)
(c) \(\left(\frac{P_{A}}{P_{B}}\right)\left(\frac{M_{B}}{M_{A}}\right)^{\frac{1}{2}}\)
(d) \(\left(\frac{\mathrm{M}_{\mathrm{A}}}{\mathrm{M}_{\mathrm{B}}}\right)\left(\frac{\mathrm{P}_{\mathrm{B}}}{\mathrm{P}_{\mathrm{A}}}\right)^{\frac{1}{2}}\)
Answer:
(c) \(\left(\frac{P_{A}}{P_{B}}\right)\left(\frac{M_{B}}{M_{A}}\right)^{\frac{1}{2}}\)
Hint:
If two gases are taken at different pressures, Graham’s law in given by \(\frac{r_{\mathrm{A}}}{r_{\mathrm{B}}}=\frac{P_{\mathrm{A}}}{P_{\mathrm{B}}}\left(\frac{\mathrm{M}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{A}}}\right)^{\frac{1}{2}}\)
![]()
Question 8.
Which of the following pairs of gases will diffuse at the same time through a poms plug?
(a) CO, NO2
(b) KO, C2H6
(c) NO2, CO2
(d) NH3, PH3
Answer:
(b) KO, C2H6
Hint:
NO and C2H6 has the same molecular mass.
Question 9.
Dominance of strong repulsive forces among molecules of gas (Z – compressibility factor)
(a) depends on Z and indicated by Z = 1
(b) depends on Z and indicated by Z > 1
(c) depends on Z and indicated by Z < 1 (d) is independent on Z Answer: (b) depends on Z and indicated by Z > 1
![]()
Question 10.
The ratio of Vander waal’s constants \(\left(\frac{a}{b}\right)\) has the dimension:
(a) atm L-1
(b) L atm mol-1
(c) atm mol L-1
(d) atm L mol-2
Answer:
(b) L atm mol-1
Hint:
\(\frac{a}{b}\)=(atm L2 mol-2) / (L mol-1) = L atm mol-1
Question 11.
The term that corrects for the attractive forces present in a real gas in the Vanderwaal’s equation is:
(a) nb
(b) \(\frac{a x^{2}}{v^{2}}\)
(c) –\(\frac{a x^{2}}{v^{2}}\)
(d) -ub
Answer:
(b) \(\frac{a x^{2}}{v^{2}}\)
Question 12.
The Vander waal’s constant ‘a’ for different gases are given below:
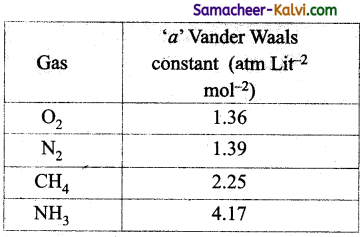
The gas that can be most easily liquefied is:
(a) O2
(b) N2
(c) CH4
(d) NH3
Answer:
(a) O2
Hint:
Greater the value of ‘a’ more easily the gas can be liquefied.
![]()
Question 13.
If helium is allo’wed to expand in vacuum, it liberates heat because:
(a) it is an inert gas
(b) it is an ideal gas
(c) the critical temperature of helium is very low
(d) it is one of the lightest gas
Answer:
(c) the critical temperature of helium is very low
Hint:
Lower the critical temperature, lower is the inversion temperature.
Question 14.
A gas such as carbon-di-oxide would be most likely to obey the ideal gas law at:
(a) low temperature and high pressures
(b) high temperature and high pressures
(c) low temperature and low pressures
(d) high temperature and low pressures
Answer:
(d) high temperature and low pressures
Hint:
Real gases show ideal behaviour at high temperature and low pressures.
![]()
Question 15.
Maximum deviations from ideal gas is ’ expected from:
(a) H2 (g)
(b) K2 (g)
(c) CH4 (g)
(d) NH3 (g)
Answer:
(d) NH3 (g)
Hint:
Of the gases given, NH3 is most easily liquefiable, i.e., has strongest intermolecular forces. Hence, it shows maximum deviation from ideal behaviour.
Question 16.
If ‘Z’ is a compressibility factor, Vander Waal’s equation at low pressures can be written as:
(a) Z = 1 + \(\frac{\mathrm{Pb}}{\mathrm{RT}}\)
(b) Z = 1 + \(\frac{\mathrm{RT}}{\mathrm{Pb}}\)
(c) Z = 1 – \(\frac{a}{V R T}\)
(d) Z = 1 – \(\frac{\mathrm{Pb}}{\mathrm{RT}}\)
Answer:
(c) 1 – \(\frac{a}{V R T}\)
Hint:
For 1 mol of a real gas, the Vander Waals equation is
(P + \(\frac{a}{\mathrm{~V}^{2}}\)) (V – b) = RT
At low pressures, V is large and therefore ‘b’ can be neglected in comparison with V.

![]()
Question 17.
The pressure exerted by 6.0 g of methane gas in a 0.03 m3 vessel at 129° C is:
(atomic masses: C = 12.01, H = 1.01 and R = 8.314 J K-1 mol-1)
(a) 215216 Pa
(b) 13409 Pa
(c) 41648 Pa
(d) 31684 Pa
Answer:
(c) 41648 Pa
Hint:
CH4 = 12.01 + 4 × 1.01 = 16.05 g mol-1
∴ 6 g of CH4 = \(\frac{6}{16.05}\) mol
T = 129°C = 273 + 129 = 402 K
PV = nRT or
P = \(\frac{n \mathrm{RT}}{\mathrm{V}}\)
P = \(\frac{6}{16.05} \times \frac{8.314 \times 402}{0.03}\)
= 41648 Pa
Question 18.
Equal volumes of He, O2 and SO2 are taken in a closed container. The ratio of the partial pressures of gases He, O2 and SO2 would be:
(a) 1 : 2 : 8
(b) 8 : 16 : 1
(c) 1 : 4 : 16
(d) 16 : 2 : 1
Answer:
(d) 16 : 2 : 1
Hint:
For a mixture of non-reacting gases partial pressure is proportional to the number of moles. If ‘m’ is the mass of each gas taken, then
No. of mol of He = \(\frac{m}{4}\)
No. of mol of O2 = \(\frac{m}{32}\)
No. of mol of SO2 = \(\frac{m}{64}\)
∴ Ratio of nHe : nO2 : nSO2 = \(\frac{1}{4}: \frac{1}{32}: \frac{1}{64}\) = 16 : 2 : 1
![]()
Question 19.
The isotherm obtained for CO is as follows:
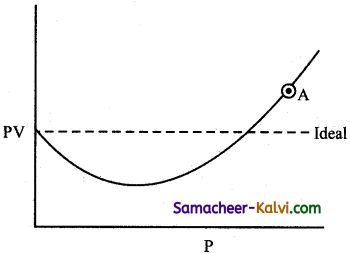
The compressibility factor for the gas at point ‘A’ will be
(a) (1 – \(\frac{b}{\mathrm{~V}}\))
(b) (1 + \(\frac{b}{\mathrm{~V}}\))
(c) (1 + \(\frac{b}{\mathrm{RT}}\))
(d) 1 + \(\frac{a}{\mathrm{RTV}}\)
Answer:
(b) (1 + \(\frac{b}{\mathrm{~V}}\))
Hint:
For a real gas, the Vander Waals, equation is
(P + \(\frac{a}{\mathrm{~V}^{2}}\))(V – b) = RT
At point A, pressure is high, so that \(\frac{a}{\mathrm{~V}^{2}}\) can be neglected, Hence,
P (V – b) = RT (or) PV – Pb = RT
(or) PV = RT + Pb
(or) \(\frac{\mathrm{PV}}{\mathrm{RT}}=1+\frac{\mathrm{Pb}}{\mathrm{RT}}\)
i.e., Z = 1 + \(\frac{\mathrm{Pb}}{\mathrm{RT}}\)
substituting P = \(\frac{\mathrm{RT}}{\mathrm{V}}\)
Z = 1 + \(\frac{b}{\mathrm{~V}}\)
![]()
Question 20.
What is the pressure of 2 mole of NH3 at 27° C when its volume is 5 litres in the Vander Waal’s equation? (a = 4.17; b = 0.03711)
(a) 10.33 atm
(b) 9.33 atm
(c) 9.74 atm
(d) 9.2 atm
Answer:
(b) 9.33 atm
Hint:
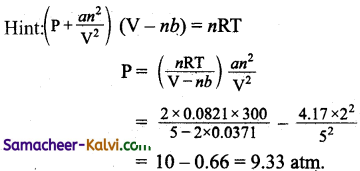
Question 21.
The temperature at which the volume of the gas becomes zero is:
(a) 0°C
(b) 0 K
(c) 0° F
(d) none of these
Answer:
(b) 0 K
![]()
Question 22.
From the following plots, identify the one which is not related to the other plots.
(a) 
(b) 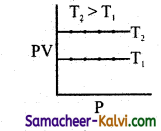
(c) 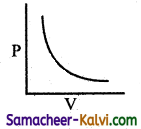
(d) 
Answer:
(d) 
Hint:
These plots shows the verification of Boyle’s law. The correct answer for (d) is T3 > T2 > T1.
Question 23.
Four equations are given below. Identify the equation which is different from the rest.
(a) \(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)
(b) \(\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\) at constant pressure
(c) Vt = V0 \(\left(\frac{273+t}{273}\right)\)
(d) \(\frac{\mathrm{V}}{\mathrm{T}}\) = Constant at constant pressure
Answer:
(a) \(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)
Hint:
While all others are different’ forms of Charles law.
![]()
Question 24.
Assertion:
At zero degree Kelvin, the volume occupied by a gas is negligible.
Reason :
All molecular motions ceases at 0K.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(c) If assertion is true but reason is false.
Hint:
Correct Statement: Vibrational motion exists ever at OK.
Question 25.
Assertion:
Compressibility factor of non ideal gases is always less than 1.
Reason :
Non ideal gases exert less pressure than expected for ideal gas.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(d) If both assertion and reason are false.
Hint:
Compressibility factor can be less than one or more than one depending on the nature of non-ideal gas.
![]()
Question 26.
Assertion:
The value of Vander Waal’s constant ‘a’ for ammonia is larger than that of nitrogen gas.
Reason:
Molecular weight of ammonia is lesser than that of nitrogen gas.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
Hint:
The inter molecular forces of attraction are greater in NH3 than those of N2.
Question 27.
Choose the incorrect statement from among the following:
(a) The hot air is lighter than that of the atmospheric air.
(b) At high altitudes as the atmospheric pressure is low, the density of air is less.
(c) Avogadro’s law helps in the separation of isotopes of Uranium.
(d) Under identical conditions, ammonia will diffuse faster than càrbon dioxide.
Answer:
(c) Avogadro’s law helps in the separation of isotopes of Uranium.
Hint:
Graham’s law of diffusion helps in the separation of isotopes of Uranium.
![]()
Question 28.
Choose the incorrect statement from among the following:
(a) The compressibility factor for carbondioxide is less than one. This means that, carbon dioxide is more compressible than expected from ideal behaviour.
(b) Greater the value of the Vanderwaal’s constant ‘a’, greater is the magnitude of inter molecular forces of attraction,
(c) A gas like carbon dioxide would be most likely to obey the ideal gas law at high temperature and low pressures. (d) Temperature below which the gas does not obey ideal gas law is called critical temperature.
Answer:
(d) Temperature below which the gas does not obey ideal gas law is called critical temperature.
Hint:
The temperature below which the gas does not obey ideal gas law is called Boyle’s temperature.
Question 29.
Choose the correct statement from the following:
(a) All gases liquefy before absolute zero is reached.
(b) At constant temperature, for a fixed mass of gas the density is inversely proportional to its pressure.
(c) In the equation \(\frac{\mathrm{V}}{\mathrm{T}}\) = Constant (k), the value of T is independent upon the amount of gas taken.
(d) The plots of pressure verses volume at constant temperature is a straight line parallel to the volume axis.
Answer:
(a) All gases liquefy before absolute zero is reached.
![]()
Question 30.
Choose the correct statement from the following:
(a) Gases showing positive deviation from ideal behaviour will have the value of the compressibility factor (Z) greater than one.
(b) Lower the value of ‘a’, greater is the ease of liquefaction.
(c) Molar volume of carbon dioxide is maximum at NTP.
(d) Aqueous tension of water depends on both the temperature and amount of water.
Answer:
(a) Gases showing positive deviation from ideal behaviour will have the value of the compressibility factor (Z) greater than one.
Question 31.
Match the entities in column I with appropriate entities in column II.
| Column I (Relationship) | Column II (Law) |
| (i) v = kT | (A) Charle’s law at constant pressure |
| (ii) PV = Constant | (B) Charles’s law |
| (iii) r ∝ \(\sqrt{1 / d}\) | (C) Boyle’s law |
| (iv) Pt ∝ T | (D) Graham’s law |
(a) (i) – (B), (ii) – (C), (iii) – (D), (iv) – (A)
(b) (i) – (C), (ii) – (D), (iii) – (A), (iv) – (B)
(c) (i) – (B), (ii) – (D), (iii) – (A), (iv) – (C)
(d) (i) – (D), (ii) – (A), (iii) – (B), (iv) – (C)
Answer:
(a) (i) – (B), (ii) – (C), (iii) – (D), (iv) – (A)
![]()
Question 32.
Match the entities in column I with appropriate entities in column II.
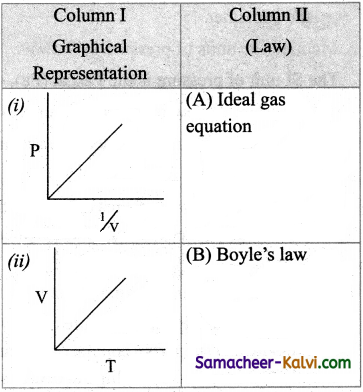
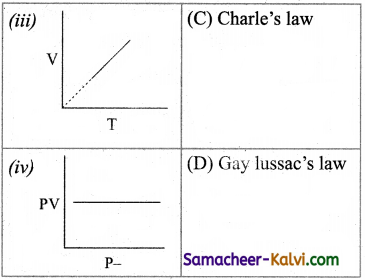
(a) (i) – (B), (ii) – (C), (iii) – (D), (iv) – (A)
(b) (i) – (C), (ii) – (B), (iii) – (A), (iv) – (D)
(c) (i) – (D), (ii) – (B), (iii) – (C), (iv) – (A)
(d) (i) – (C), (ii) – (D), (iii) – (B), (iv) – (A)
Answer:
(a) (i) – (B), (ii) – (C), (iii) – (D), (iv) – (A)