TN Board 12th Physics Important Questions Chapter 8 Atomic and Nuclear Physics

TN State Board 12th Physics Important Questions Chapter 8 Atomic and Nuclear Physics

Question 1.
Why did Thomson’s atomic model fail?
Answer:
Thomson model failed to explain the scattering of α-particles through large angles in Rutherford’s experiment.

Question 2.
Why is it that mass of the nucleus does not enter the formula for impact parameter, but in change does?
Answer:
The scattering occurs due to the electrostatic field of the nucleus. That is why charge of nucleus enters the expression for the impact parameter.

Question 3.
The kinetic energy of α-particle incident on gold foil is doubled. How does the distance of closest approach charge?
Answer:
As the distance of closest approach is inversely proportional to the kinetic energy of the incident a-particle, so the distance of closest approach is halved when the kinetic energy of a-particle is doubled.

Question 4.
Why is electron revolving round the nucleus of an atom?
Answer:
If the electrons were stationary, they would fall into the nucleus due to the electrostatic attraction and the atom would be unstable.

Question 5.
What is the significance of the negative energy of electron in the orbit?
Answer:
The negative energy signifies that the electron is bound to the nucleus. Due to electrostatic attraction between electron and nucleus, the potential energy is negative and is greater than kinetic energy of electron. The total energy of electron is negative. It cannot escape from the atom.

Question 6.
How much is the energy possessed by an electron for n = ∞?
Answer:
For n = ∞,
E_n = \(-\frac{13.6}{n^{2}}=\frac{-13.6}{\infty}\) = 0
Its energy is zero.

Question 7.
Define ionization energy How would the ionisation energy charge when electron in hydrogen atom is replaced by a particle of mass 200 times that of the electron but having the same charge.
Answer:
Ionisation energy is defined as the energy required to free an electron from the ground state of an atom.
i. e., IE = E_∞ – E₁ = \(\frac{2 \pi^{2} m k^{2} e^{4}}{h^{3}}\)
i.e., IE ∝ m
Thus, the I.E will become 200 times that of the electron.

Question 8.
The ground state energy of hydrogen atom is -13.6 eV. What are the kinetic and potential energies of the electron in his state?
Answer:
Total energy, E = -13.6 eV
K.E = – E = – (-13.6) =13.6 eV
P.E = – 2.K.E = – 2 x 13.6 = – 27.2 eV

Question 9.
What holds nucleons together in a nucleus?
Answer:
The strong attractive nuclear force holds the nucleons together inside a nucleus which even over comes the electrostatic repulsion between the protons.

Question 10.
Why is the mass of a nucleus always less than the sum of the masses of its constituents, neutrons and protons?
Answer:
When nucleons approach each other to form a nucleus, they strongly attract each other. Their potential energy decreases and becomes negative. It is their potential energy which holds the nucleons together in the nucleus. The decrease in potential energy results in the decrease in the mass of the nucleons inside the nucleus.

Question 11.
A nucleus contains no electrons, yet it ejects them. How?
Answer:
A neutron of a nucleus decays into a proton, an electron arid an antineutrino. It is this electron which is emitted as β-particle.
\({ }_{0}^{1} n \rightarrow{ }_{1}^{1} p+{ }_{-1}^{0} e+\bar{v}\)

Question 12.
Why is nuclear fusion difficult to carry out?
Answer:
Nuclear fusion requires very high temperature of 106 – 107 K. This temperature is attained by causing explosion due to the fission process. Moreover, no solid container can withstand such a high temperature.

Question 13.
How sun is constantly lossing mass due to thermonuclear fusion?
Answer:
In each fusion reaction, a small mass of the Sun changes into thermal energy. So Sun is constantly losing mass due to thermonuclear fusion.

Question 14.
State the reason, why heavy water is I generally used as a moderator in a nuclear reactor.
Answer:
Heavy water contains protons (of mass nearly that of neutrons). Fast moving neutrons undergo elastic collisions with these slow moving neutrons and thus get slowed down. Hence heavy water can be used as a moderator. Also, heavy water has negligible cross section for neutron absorption.

Question 15.
When \({ }_{3}^{7} \mathrm{Li}\) is bombarded with a certain particle, two alpha particle are produced, identify the bombarding particle.
Answer:
Let \({ }_{Z}^{A} \mathrm{P}\) be the bombarding particle.
Then, \({ }_{3}^{7} \mathrm{Li}+\underset{\mathrm{Z}}{\mathrm{A}} \mathrm{P}_{2}^{4} \mathrm{He}+{ }_{2}^{4} \mathrm{He}\)
Using the laws of conservation of mass and energy, we get
A + 7 = 4 + 4
A = 1
Z + 3 = 2 + 2
Z = 1
Thus, the bombarding particle is proton (\({ }_{1}^{1} \mathrm{Li}\)).

Question 16.
A radioactive substance has a half-life period of 30 days. What is the disintegration constant?
Answer:
Decay constant λ = \(\frac{0.693}{\mathrm{~T}_{1 / 2}}\)

= \(\frac{0.693}{30}\) = 0.0231 day^-1

Question 17.
The half-life period of a radioactive substance is 60 days. What is the time taken for(\(\frac{3}{4}\))th of its original mass to disintegrate?
Answer:

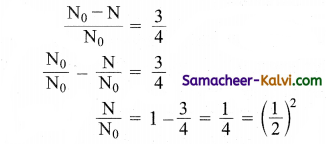
∴ Number of half-lives, n = 2
Time of disintegration = Half-life × No. of half-lives = 60 × 2 = 120 days.

Question 18.
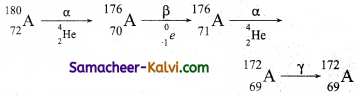
A radioactive nucleus A undergoes a series of decays according to the following scheme.

The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A₄.
Answer:
Mass number of A₄ = 172
Atomic number of A₄ = 69

Question 19.
Complete the following reactions:
(a) \({ }_{5}^{10} \mathrm{~B}+{ }_{0}^{1} n \rightarrow{ }_{2}^{4} \mathrm{He}+\ldots\)
(b) \({ }_{42}^{94} \mathrm{M}_{0}+{ }_{1}^{2} \mathrm{H} \rightarrow{ }_{43}^{95} \mathrm{Te}+\ldots\)

(a) \({ }_{5}^{10} \mathrm{~B}+{ }_{0}^{1} n \rightarrow{ }_{2}^{4} \mathrm{He}+\ldots\)
Answer:
Atomic number: 5 + 0 – 2 = 3
Mass number: 10+1-4 = 7
Since atomic number is 3, element is Li.

(b) \({ }_{42}^{94} \mathrm{M}_{0}+{ }_{1}^{2} \mathrm{H} \rightarrow{ }_{43}^{95} \mathrm{Te}+\ldots\)
Answer:
Mass number: 94 + 2 – 95 = 1
Atomic number: 42 + 1 – 43 = 0
Since atomic number is 0, it represents neutron.

Question 20.
If the mass defect of the nucleus ¹²₆C is 0.088 amu, then calculate the binding energy per nucleon.
Answer:
mass defect of ¹²₆C ∆m = 0.088 amu
B.E of the nucleus = 0.088 × 931 MeV
B.E per nucleon = \(\frac{0.088 \times 931}{12}\)
= 6.827 MeV

Question 21.
Distinguish atom bomb from nuclear reactor.
Answer:

Atom Bomb	Nuclear reactor
It is used for destructive purpose.	It is used for constructive power. It is used to produce electric power and radio isotopes.
The chain reaction in it is uncontrolled.	The chain reaction in it is controlled.

Question 22.
Distinguish between nuclear fission and fusion.
Answer:

Nuclear fission	Nuclear Fusion
The process of breaking up of the nucleus of a heavy atom into two fragments with the release of large amount of energy is known as nuclear fission.	The process in which two or more lighter nuclei combine to form a heavier nucleus.
Neutrons are the link particle of this process.	Protons are the link particles of this process.
It is quick process.	It occurs in several steps. There is sufficient time gap between initial and final step.
It produce very harmful radioactive wastes.	The products of fusion are harmless.
Here the energy available per nucleon is small, about 0.85 MeV	Here the energy available per nucleon is large, about 6.75 MeV

Question 23.
Fusion energy is a clean energy. Why?
Answer:
As lighter atomic nuclei are involved in the reaction, harmful radiations are not given out during fusion reaction. So, we say that fusion energy is a clean energy.

Question 24.
What is the use of a control rod in the reactor? Mention any two control rods.
Answer:
Control rods are used to control the chain reactions. They are good absorbers of neutrons. Eg: Boron, Cadmium.

Question 25.
(a) The energy levels of an atom are as shown below. Which of them will result in the transition of a photon of wavelength 275 nm?

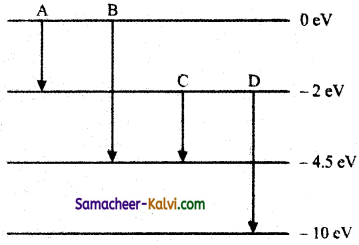
(b) Which transition corresponds to emission of radiation of (i) maximum wavelength and (ii) minimum wavelength.
Answer:
(a) The energy E of a photon of wavelength 275 nm is given by
E = \(\frac{h c}{\lambda}\)

= \(\frac{6.626 \times 10^{-34} \times 3 \times 10^{8}}{275 \times 10^{-9} \times 1.6 \times 10^{-19}}\) eV
= 4.5 eV
This energy corresponds to the transition B for which the energy change.

(b) E = \(\frac{h c}{\lambda}\)
i.e., E ∝ \(\frac{1}{\lambda}\)
⇒ λ ∝\(\frac{1}{\mathrm{E}}\)
λ_min ∝ \(\frac{1}{\mathrm{E}_{\min }}\) and
λ_min ∝ \(\frac{1}{\mathrm{E}_{\max }}\)

(i) Transition A, for which the energy emission is minimum, corresponds to the emission of radiation of maximum wavelength.
(ii) Transition D, for which the energy emission is maximum, corresponds to the emission of radiation of minimum wavelength.

Question 26.
Find the relation between the three wavelength λ₁, λ₂ and λ₃ from the energy level diagram shown below:

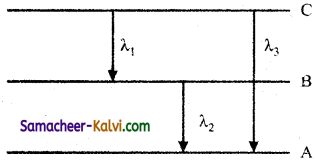
Answer:

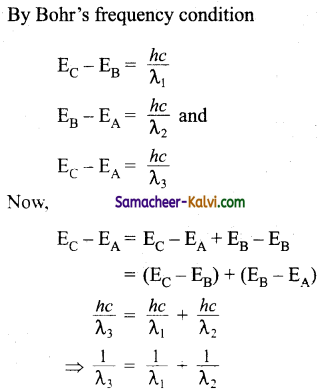
Question 27.
The wavelength of the second line of the Balmar series in the hydrogen spectrum is 4861 Å. Calculate the wavelength of the first line.
Answer:
The wavelength λ₁ and λ₂ of the first and second lines of the Balmer series are given by

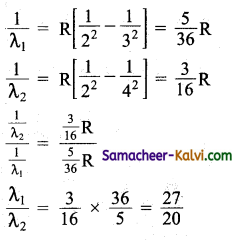
λ₁ = \(\frac{27}{20}\) × λ₂

λ₁ = \(\frac{27}{20}\) × 4861 = 6562 Å

Question 28.
What is the minimum energy that must be given to a H-atom in ground state so that it ean emit an in Salmar series?
If the angular momentum of the system is conserved, what would be the angular momentum of such H_r photon?
Answer:
H_r in Balmar series corresponds to transition, n = 5 to n = 2. So the electron in ground state n = 1 must first be put in the state n = 5.
Energy required = E₁ – E₅ = 13.6 – 0.54 = 13.06 eV

If the angular momentum is conserved, angular momentum of photon change in angular momentum of electron.
L₅ – L₁ = \(\frac{5 h}{2 \pi}-\frac{2 h}{2 \pi}=\frac{3 h}{2 \pi}\)
= \(\frac{3 \times 6.63 \times 10^{-34}}{2 \times 3.14}\)
= 3.167 × 10^-34 kg m² s^-1

Question 29.
The decay constant, for a radio nuclide element, has a value 1.386 day^-1. After how much time will a given sample of this radio nuclide get reduced to only 6.25% of its present number.
Answer:
Have λ = 1.386 day
T_1/2 = \(\frac{0.693}{\lambda}=\frac{0.693}{1.386}\) = 0.5 day

\(\frac{\mathrm{N}}{\mathrm{N}_{0}}\) = 6.25 %
= \(\frac{6.25}{100}=\frac{1}{16}\)
= \(\left(\frac{1}{2}\right)^{4}\)
∴ n = 4
t = n T_1/2
= 4 × 0.5 = 2 days.

Question 30.
The half life of \({ }_{92}^{238} \mathrm{U}\) against ∝-decay is 1.5 × 10⁷ s. What is the activity of a sample of \({ }_{92}^{238} \mathrm{U}\) having 2.5 × 10²⁰ atoms.
Answer:
Here, T_1/2 = 1.5 × 10¹⁷ s
N = 2.5 × 10²⁰ atoms
∴ R = λN = \(\frac{0.693}{\mathrm{~T}_{1 / 2}}\) × N
= \(\frac{0.693 \times 25 \times 10^{20}}{1.5 \times 10^{17}}\)
= 11.55 × 10³
= 11550 disintegrations / sec

Question 31.
The half life of \({ }_{92}^{238} \mathrm{U}\) ∝-decay is 4.5 × 10⁹ years. Calculate the activity of 1g sample of \({ }_{92}^{238} \mathrm{U}\).
Answer:
Here T_1/2 = 4.5 × 10⁹ years
= 4.5 × 10⁹ × 365 × 24 × 3600
= 1.419 × 10¹⁷ s
m = 1 g
M = 238
Number of atoms in 1 g uranium
N = \(\frac{m}{\mathrm{M}}\) × Avogadro’s number
= \(\frac{1 \times 6.023 \times 10^{23}}{238}\)
= 2.5306 × 10²¹ atoms.

Activity of the sample
R = λN = \(\frac{0.693}{\mathrm{~T}_{1 / 2}}\) × N

= \(\frac{0.693 \times 2.5306 \times 10^{21}}{1.419 \times 10^{17}}\)
= 1.235 × 10⁴ Bq.

Question 32.
If the binding energy of the electron in a hydrogen atom is 13.6 eV, what is the energy required to remove the electron from the first excIted state of Li⁺⁺ ion.
Answer:
E_n = \(\frac{13.6}{n^{2}} \mathrm{Z}^{2}\)
for first excited state, n = 2
for Li⁺⁺ Z = 3
∴ E = \(\frac{13.6}{4}\) × 9 = 30.6 eV

Question 33.
What is the ratio of frequencies of long wavelength limits of Lyman and Balmar series of hydrogen spectrum.
Answer:
For Lyman series
υ_Lyman = \(\frac{c}{\lambda_{\max }}\)
= Rc[latex]\frac{1}{1^{2}}-\frac{1}{2^{2}}[/latex]
= \(\frac{3 \mathrm{R} c}{4}\)
For Balmer series

Question 34.
A heavy nucleus X of miss number A = 240 and binding energy per nucleon 7.6 MeV is split into two nearly equal fragment Y and Z of mass number A₁ = 110 and A₂ = 130, The binding energy of each one of these nuclei is 8.5 MeV per nucleon. Calculate the total binding energy of each of the nuclei X, Y and Z find hence the energy Question released per fission in MeV.
Answer:
For nucleus X : A = 240
B.E per nucleon = 7.6 MeV
Total B.E of X = 240 × 7.6 = 1824 MeV
For nucleus Y : A₁ = 110
B.E per nucleon = 8.5 MeV
Total B.E of Y = 110 × 8.5 = 935 MeV
For nucleus Z : A₂ = 130
B.E per nucleon = 8.5 MeV
Total B.E of Z = 130 × 8.5 = 1105 MeV
Energy released per fission,
Question = B.E of Y + B.E of Z – B.E of X = 935 + 1105 – 1824 = 216 MeV

Question 35.
With the help of a diagram, describe discharge tube. What is the origin of cathode rays?
Answer:
A simple and convenient device used to study the conduction of electricity through gases is known as gas discharge tube. It is a electrodes C and A are fitted inside the tube at the ends. The side tube is connected to a high vacuum pump and a low pressure gauge. The electrodes C and A are fitted inside the tube at the ends. The side tube is connected to a high vacuum pump and a low pressure gauge. The electrodes C and A are connected to the secondary of a powerful induction coil, which maintains a potential difference of 50 kV. The electrode C connected to the negative terminal of the induction coil is called cathode and the electrode A connected to the positive terminal is called the anode.

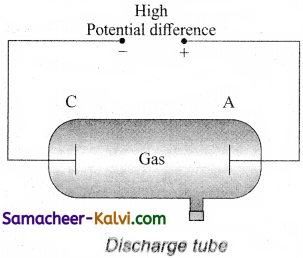
Suppose the pressure of the gas in discharge tube is reduced to around 110 mm of Hg using vacuum pump, it is observed that no discharge takes place, when the pressure is kept near 100mm of Hg, the discharge electricity through the tube takes place. Consequently, irregular streaks of light appear and also crackling sound is produced. When the pressure is reduced to the order of 10 mm of Hg, a luminous column known as positive column is formed from anode to cathode.

When the pressure reaches to around 0.1 mm of Hg, positive column disappears. At this time, a dark space is formed between anode and cathode which is often called crooke’s dark space and the walls of the tube appear with green colour. At this stage, some invisible rays emanates from cathode called cathode rays, which are later found be a beam of electrons.

Question 36.
Describe Thomson’s model of an atom. Why was this model discarded later on?
Answer:
J.J. Thomson proposed that an atom is a sphere is a sphere of positively charged matter with electrons embedded in it. The j positive charge is uniformly distributed over the entire atom. The arrangement of electrons inside the continuous positive charge is similar to that of the seeds in a watermelon or the plums in a pudding.

The electrons are arranged in such a manner that their mutual repulsions are balanced by their attractions with the positively charged matter. Thus the atom as a whole is stable and neutral.

Thomson’s model was able to explain with some success the process like chemical reaction and radioactive disintegration. According to this model, all the charges are assumed to be at rest. But from classical electrodynamics, no stable equilibrium points exist in electrostatic configuration and hence such an atom cannot be stable.

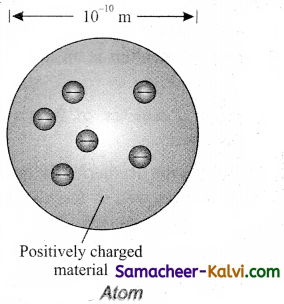
Failure of Thomsons model:
(i) It could not explain the origin of several spectral series in the case of hydrogen and other atoms.
(ii) It failed to explain the large angle scattering of a-particles in Rutherford’s experiment.

Question 37.
Describe Rutherford’s experiment on the scattering of a-partieie by a nucleus. Ext fain the observations and conclusions of the experiment.
Answer:
Experimental arrangement:
A schematic arrangement of the Geiger – Marsden experiment is shown in figure.

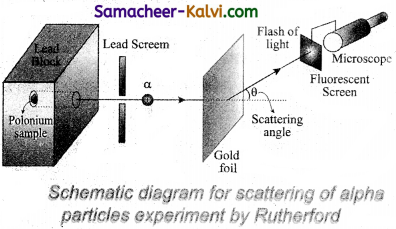
A radioactive source of a-particles polonium is enclosed in thick lead block, provided with a narrow opening. The a-particles from this source are collimated into a narrow beam through a narrow slit. The beam is allowed to fall on a thin gold foil of thickness 2.1 × 10^-7 m. The ∝-particles scattered in different directions are observed with the help of a rotatable detector which consists of a zinc sulphide screen and a microscope.

Whenever an a-particle strikes the screen, it produces a tiny flash or scintillation, which is viewed through the microscope. In this way, the number of ∝-particles scattered at different angles can be counted. The whole apparatus is enclosed in an evacuated chamber to avoid scattering of a-particles by air molecules.

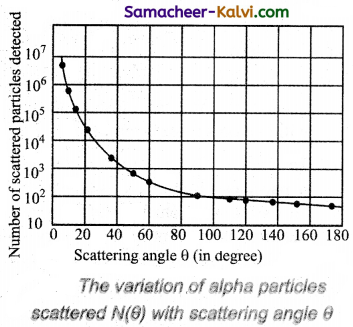
Observations:
As shown in figure, a graph is drawn between the scattering angle θ and the number N (θ) of the a-particles scattered at angle θ, for a very large number of a-particles. The dotted points are the alpha scattering experiment data points obtained by Geiger and Marsden and the solid curve is the prediction from Rutherford’s nuclear model. It is observed that the Rutherford’s nuclear model is in good agreement with the experimental data.

The above graph reveals the following facts:
(i) Most of the alpha particles are undeflected through the gold foil and went straight.
(ii) Some of the alpha particles are deflected through a small angle.
(iii) A few alpha particle (one is thousand) are deflected through the angle more than 90°.
(iv) Very few alpha particles returned back from the gold foil, scattering a deflection of nearly 180°.

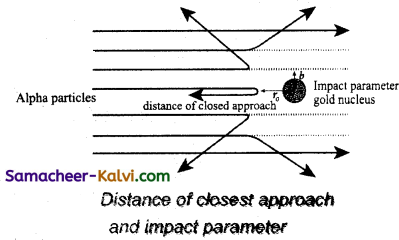
Significance of the result:
Rutherford concluded the following important falls about an atom.
(i) As most of the α-particles pass straight through the foil, so most of the space within atoms must be empty.
(ii) To explain large angle scattering of α-particles, Rutherford suggested that all the positive charge and the mass of the atom is concentrated in a very small region, called the nucleus of the atom.
(iii) The nucleus is surrounded by a cloud of electrons whose total negative charge is equal to the total positive charge on the nucleus so that the atom as a whole is electrically neutral.

Question 38.
Obtain Bohr’s quantisation condition on the basis of the wave picture of an electron.
Answer:
Consider -the motion of an electron in a circular orbit of radius r around the nucleus of the atom. According to de Broglie hypothesis, this electron is also associated with wave character.

Hence a circular orbit can be taken to be a stationary energy state only if it contains an integral number of de- Broglie wavelength.

i.e., we must have 2πr = nλ
But de-Broglie wavelength λ = \(\frac{h}{m v}\)
∴ 2πr = \(\frac{n h}{m v}\)
mvr = \(\frac{n h}{2 \pi}\)

∴ The angular momentum L of the electron must be L = mvr = \(\frac{n h}{2 \pi}\) = 1, 2, 3 …

This is the famous Bohr’s quantisation condition for angular momentum. Thus only those circular orbits can be the allowed stationary states of an electron in which its angular momentum is an integral multiples of \(\frac{h}{2 \pi}\)

Question 39.
State the postulates of Bohr’s theory of hydrogen atom.
Answer:
Accepting the Rutherford’s nucleus model of an atom as well as the planck’s quantum theory, Bohr proposed an atomic model to explain the spectra emitted by hydrogen atom. Bohr’s atom model, so called planetary model of the atom, is based on the following postulates.

(i) Nuclear concept:
An atom consists of a small and massive central core, called nucleus around which planetary electrons revolve. The centripetal force required for their rotation is provided by the electrostatic attraction between the electrons and the nucleus.

(ii) Quantum condition:
Of all the possible circular orbits allowed by the classic theory, the electrons are permitted to circulate only in those orbits in which the angular momentum of an electron is an integral multiple of \(\frac{h}{2 \pi}\), h being planck’s constant.
∵ For any permitted orbit L = mvr = \(\frac{n h}{2 \pi}\)
Where n is positive integer called principal quantum number. The above equation is quantum condition.

(iii) Stationary orbits:
while revolving around the nucleus in the permissible orbits, an electron does not radiate energy. These non-radiating orbits are called stationary orbits.

(iv) Frequency condition:
An atom can emit or absorb radiation in the form of discrete energy photon only when an electron jumps from a higher to lower orbit or from a lower to a higher orbit, respectively. If E x and E2 are the energies associated with these permitted orbits, then the frequency v of the emitted or absorbed radiation is given by
hυ = E₂ – E₁
This is Bohr’s frequency condition.

Question 40.
Using Bohr’s postulates, drive an expression for the radii of the permitted orbits in the hydrogen atom. What is Bohr’s radius?
Answer:

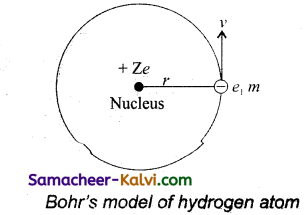
According to Bohr’s theory, a hydrogen atom consists of a nucleus with a positive charge Ze, and a single electron of charge -e, which revolves around it in a circular orbit of radius r_n. Here Z is the atomic number and for hydrogen Z = 1.

The electrostatic force of attraction between the nucleus and the electron is

F = \(\frac{k . Z e . e}{r_{n}^{2}}=\frac{k Z e^{2}}{r_{n}^{2}}\)

To keep the electron in its orbit, the centripetal force on the electron must be equal to the electrostatic attraction.

\(\frac{m v_{n}^{2}}{r_{n}}=\frac{k Z e^{2}}{r_{n}^{2}}\)
mv_n² = \(\frac{k Z e^{2}}{r_{n}^{2}}\)
r_n = \(\frac{k Z e^{2}}{m v_{n}^{2}}\) …………..(1)

Where m is the mass of the electron and v_n, its speed in an orbit of radius r_n
Bohr’s quantisation condition for angular spectrum is

This is known as Bohr radius which is the smallest radius of the orbit in an atom. Bohr radius is also used as unit of length called Bohr. For hydrogen atom (Z = 1) the radius of nth orbit is r_n = a₀n²

Clearly, the radii of the permitted orbits are proportional to n² and increase in the ratio of 1 : 4 : 9 : 16 … where n is called the principle quantum number.

Multiple Choice Questions:

Question 1.
The value of 1 amu is:
(a) 937 eV
(b) mass of carbon atom
(c) mass of one proton
(d) 1.60 × 10^-27 kg
Answer:
(d) 1.60 × 10^-27 kg

Question 2.
In the following nuclear reaction \({ }_{13}^{27} \mathrm{~A} l+{ }_{2}^{4} \mathrm{He} \rightarrow \mathrm{X}+{ }_{0}^{1} n\) the element X is:
(a) \({ }_{15}^{30} \mathrm{S}\)

(b) \({ }_{15}^{30} \mathrm{P}\)

(c) \({ }_{15}^{30} \mathrm{S}\)

(d) \({ }_{15}^{29} \mathrm{Si}\)

Answer:
(a) \({ }_{15}^{30} \mathrm{S}\)

Question 3.
The time taken by the radioactive element to reduce to \(\frac{1}{e}\) times is:
(a) half-life
(b) mean life
(c) half-life/2
(d) 2 mean life
Answer:
(b) mean life

Question 4.
The moderator used in nuclear reactor is:
(a) cadmium
(b) boron carbide
(c) heavy water
(d) uranium \({ }_{92}^{235} \mathrm{U}\)
Answer:
(c) heavy water

Question 5.
The nuclei \({ }_{13}^{27} \mathrm{Si}\) and \({ }_{14}^{28} \mathrm{Si}\) are examples of:
(a) isotopes
(b) isobars
(c) isotones
(d) isomers
Answer:
(c) isotones

Question 6.
The mean life (τ) and half life (T1/2) of a radioactive element are related as:
(a) τ = 2T_1/2

(b) τ = \(\frac{\mathrm{T}_{1 / 2}}{0.6937}\)

(c) τ = \(\frac{\mathrm{T}_{1 / 2}}{2}\)

(d) τ = 0.6931 T_1/2
Answer:
(b) τ = \(\frac{\mathrm{T}_{1 / 2}}{0.6937}\)

Question 7.
The binding energy of nucleus is:
(a) 8.8 MeV
(b) 88 MeV
(c) 41.3 MeV
(d) 493 MeV
Answer:
(d) 493 MeV

Question 8.
Which of the following is not a moderator?
(a) Water
(b) Heavy water
(c) Liquid sodium
(d) Graphite
Answer:
(c) Liquid sodium

Question 9.
Wave number is defined as the number of waves:
(a) produced in one second
(b) in a distance of 1 metre
(c) in a distance of 3 × 10⁸ metre
(d) in a distance of X metre
Answer:
(b) in a distance of 1 metre

Question 10.
In hydrogen atom, which of the following transitions produce spectral line of maximum frequency?
(a) 2 → 1
(b) 6 → 2
(c) 4 → 3
(d) 5 → 1
Answer:
(d) 5 → 1

Question 11.
The ratio of areas enclosed by first three Bohr orbits of hydrogen atom is:
(a) 1 : 2 : 3
(b) 1 : 16 : 81
(c) 1 : 8 : 27
(d) 1 : 4 :9
Answer:
(b) 1 : 16 : 81

Question 12.
According to Bohr’s postulates, which of the following quantities take discrete values?
(a) Kinetic energy
(b) Potential energy
(c) Angular momentum
(d) Momentum
Answer:
(c) Angular momentum

Question 13.
The first excitation potential energy or the minimum energy required to excite the atom from ground state of hydrogen atom is:
(a) 13.6 eV
(b) 10.2 eV
(c) 3.4 eV
(d) 1.89 eV
Answer:
(b) 10.2 eV

Question 14.
The ratio of the radii of the first three Bohr orbits is:
(a) 1 : \(\frac{1}{2}\) : \(\frac{1}{3}\)
(b) 1 : 2 : 3
(c) 1 : 8 : 27
(d) 1 : 4 : 9
Answer:
(d) 1 : 4 : 9

Question 15.
The time taken by a radioactive element to reduce to e~’A times its original amount is its:
(a) half-life period
(b) \(\frac{\text { half – life period }}{2}\)
(c) mean life period
(d) \(\frac{\text { mean life period }}{2}\)
Answer:
(d) \(\frac{\text { mean life period }}{2}\)

Question 16.
In which of the following systems will the radius of the first orbit (n= 1) be minimum?
(a) single ionized helium
(b) double ionized lithium
(c) deuterium atom
(d) hydrogen atom
Answer:
(b) double ionized lithium

Question 17.
In Bohr’s model, if the atomic radius of the first orbit is rQ, then the radius of the fourth orbit is:
(a) 16 r₀
(b) 4 r₀
(c) r₀
(d) \(\frac{r_{0}}{16}\)
Answer:
(a) 16 r₀

Question 18.
In Bohr model of hydrogen atom, the ratio of periods of revolution of an electron in n = 2 and n = 1 orbits is:
(a) 2 : 1
(b) 4 : 1
(c) 8 : 1
(d) 16 : 1
Answer:
(c) 8 : 1

Question 19.
What is the angular momentum of an electron in Bohr’s hydrogen atom whose energy is – 0.544 eV:
(a) \(\frac{h}{\pi}\)

(b) \(\frac{2 h}{\pi}\)

(c) \(\frac{5 h}{\pi}\)

(d) \(\frac{7 h}{\pi}\)

Answer:
(c) \(\frac{5 h}{\pi}\)

Question 20.
Minimum excitation potential of Bohr’s first orbit in hydrogen atom is:
(a) 10.2 V
(b) 13.6 V
(c) 3.6 V
(d) 3.4 V
Answer:
(a) 10.2 V

Question 21.
The ratio of the frequencies of the long wavelength limits of Lyman and Balmer series of hydrogen spectrum is:
(a) 5 : 27
(b) 27 : 5
(c) 4 : 1
(d) 1 : 4
Answer:
(b) 27 : 5

Question 22.
The ground state energy of hydrogen atom is -13.6 eV what is the potential energy of the electron is this state?
(a) 0 eV
(b) – 27.2 eV
(c) 1 eV
(d) 2 eV
Answer:
(b) – 27.2 eV

Question 23.
Radius of first orbit is r. What is the radius of 2^nd Bohr orbit?
(a) 4r
(b) 8r
(c) 2r
(d) 16r
Answer:
(a) 4r

Question 24.
In Bohr model of hydrogen atom, the force on the electron depends on the principal quantum number as:
(a) F ∝ \(\frac{1}{n^{3}}\)

(b) F ∝ \(\frac{1}{n^{4}}\)

(c) F ∝ \(\frac{1}{n^{5}}\)

(b) F ∝ \(\frac{1}{n^{2}}\)
Answer:
(b) F ∝ \(\frac{1}{n^{4}}\)

Question 25.
Orbital acceleration \(\left(\frac{v^{2}}{r}\right)\) of electron is:
(a) \(\frac{n^{2} h^{2}}{4 \pi^{2} m^{2} r^{3}}\)

(b) \(\frac{n^{2} h^{2}}{2 n^{2} r^{3}}\)

(c) \(\frac{4 n^{2} h^{2}}{\pi^{2} m^{2} r^{3}}\)

(d) \(\frac{4 n^{2} h^{2}}{4 \pi^{2} m^{2} r^{3}}\)

Answer:
(a) \(\frac{n^{2} h^{2}}{4 \pi^{2} m^{2} r^{3}}\)

Question 26.
In a beryllium atom, if a0 be the radius of the first orbit, then the radius of the second orbit will be:
(a) na₀
(b) a₀
(c) n²a₀
(d) \(\frac{a_{0}}{n^{2}}\)
Answer:
(c) n²a₀

Question 27.
The ionisation potential for second He electron is:
(a) 13.6 eV
(b) 27.2 eV
(c) 100 eV
(d) 54.4 eV
Answer:
(d) 54.4 eV

Question 28.
The ratio of the energies of the hydrogen atom is in first to second excited state is:
(a) \(\frac{1}{4}\)

(b)\(\frac{4}{9}\)

(c) \(\frac{9}{4}\)

(d) 4
Answer:
(c) \(\frac{9}{4}\)

Question 29.
The radius of electron’s second stationary orbit in Bohr’s atom is R. The radius of the third orbit will be:
(a) 3 R
(b) 2.25 R
(c) 9 R
(d) \(\frac{R}3}\)
Answer:
(b) 2.25 R

Question 30.
In any Bohr orbit of the hydrogen atom, the ratio of kinetic energy to potential energy of the electron is:
(a) \(\frac{1}{2}\)
(b) 2
(c) –\(\frac{1}{2}\)
(d) -2
Answer:
(c) –\(\frac{1}{2}\)

Question 31.
In \({ }_{88} \mathrm{Ra}^{226}\) nucleus, there are:
(a) 138 protons and 88 neutrons
(b) 138 neutrons and 88 protons
(c) 226 protons and 88 electrons
(d) 226 neutrons and 138 electrons
Answer:
(b) 138 neutrons and 88 protons

Question 32.
Outside a nucleus:
(a) neutron is stable
(b) proton and neutron both are stable
(c) neutron is unstable
(d) neither neutron nor proton is stable
Answer:
(c) neutron is unstable

Question 33.
Nuclear force are:
(a) short ranged independent attractive and charge independent
(b) short ranged dependentattractive and charge independent
(c) long ranged independent repulsive and charge independent
(d) long ranged dependent repulsive and charge dependent
Answer:
(a) short ranged independent attractive and charge independent

Question 34.
In nuclear reaction, \({ }_{2}^{4} \mathrm{He}+{ }_{\mathrm{Z}} \mathrm{A} \rightarrow{\mathrm{z}}+2 \mathrm{Y}^{\mathrm{A}+3}+\mathrm{A}\) A denotes:
(a) electron
(b) positron
(c) proton
(d) neutron
Answer:
(d) neutron

Question 35.
Complete the reaction:
\(n+{ }_{92}^{235} \mathrm{U} \rightarrow{ }_{56}^{144} \mathrm{Ba}+\ldots+3 n\)
(a) \({ }_{36} \mathrm{Kr}^{89}\)

(b) \({ }_{36} \mathrm{Kr}^{90}\)

(c) \({ }_{36} \mathrm{Kr}^{91}\)

(d) \({ }_{36} \mathrm{Kr}^{92}\)
Answer:
(a) \({ }_{36} \mathrm{Kr}^{89}\)

Question 36.
In the nuclear reaction \({ }_{6} \mathrm{C}^{11} \rightarrow{ }_{5} \mathrm{~B}^{11}+\mathrm{B}^{+}+\mathrm{X}\) what does X stand for:
(a) an electron
(b) a proton
(c) a neutron
(d) a neutrino
Answer:
(d) a neutrino

Question 37.
1g of hydrogen is converted into 0.993 g of helium in a thermonuclear reaction. The energy released is:
(a) 63 × 10⁷ J
(b) 63 × 10¹⁰ J
(c) 63 × 10¹⁴ J
(d) 63 × 10²⁰ J
Answer:
(b) 63 × 10¹⁰ J

Question 38.
In the given reaction \({ }_{z} \mathrm{X}^{\mathrm{A}} \rightarrow{ }_{\mathrm{z}+1} \mathrm{Y}^{\mathrm{A}} \rightarrow{ }_{\mathrm{z}-1} \mathrm{~K}^{\mathrm{A}-4} \rightarrow_{\mathrm{z}-1} \mathrm{~K}^{\mathrm{A}-4}\) Radioactive radiations are emitted in the sequence:
(a) α, β, γ
(b) β, α, γ
(c) γ, α, β
(d) β, γ, α
Answer:
(b) β, α, γ

Question 39.
The ratio of the surface area of the nuclei (assuming spherical shape) Zn64 and Al27 is:
(a) 9 : 16
(b) 16 : 9
(c) 64 : 27
(d) 4 : 3
Answer:
(b) 16 : 9

40.
A sample of uranium containing both the isotopes U²³⁵ and U²³⁸ is bombarded with a slow neutron. Then the isotope that fission readily is:
(a) U²³⁵
(b) U²³⁸
(c) both U²³⁵ and U²³⁸
(d) neither U²³⁵ nor U²³⁸
Answer:
(a) U²³⁵

41.
Match List -I with List -II and then select the correct answer using the codes given below:

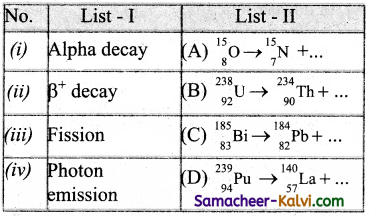
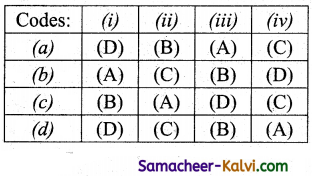
Answer:
(c)

Question 42.
Match List – I with List – II.

List I	List II
(i) Isotopes	(A) same number of neutrons
(ii) Isotones	(B) ∆m/A
(iii) Binding energy	(C) same number of atomic number
(iv) Pracking fraction	(D) same number of mass number
	(E) ∆m/c2

(a) (i) – (C); (ii) – (A); (iii) – (B); (iv) – (E)
(b) (i) – (C); (ii) – (A); (iii) – (D); (iv) – (B)
(c) (i) – (C); (ii) – (A); (iii) – (B); (iv) – (E)
(d) (i) – (B); (ii) – (C); (iii) – (D); (iv) – (E)
Answer:
(a) (i) – (C); (ii) – (A); (iii) – (B); (iv) – (E)

Question 43.
Which one of the following statements is wrong in the context of X rays generated from a X-ray tube?
(a) Wavelength of characteristic X-ray decreases when the atomic number of the target increases.
(b) Cut-off wavelength of the continuous X-rays depends on the atomic number of the target.
(c) Intensity of the characteristic X-rays depends on the electrical power given to the X-ray tube.
(d) Cut-off wavelength of the continuous X-rays depends on the energy of the electrons in the X-ray tube
Answer:
(b) Cut-off wavelength of the continuous X-rays depends on the atomic number of the target.

Question 44.
Which one of the following statements is wrong in the context of Bohr’s model of hydrogen atom.
(a) the radius of the n^th orbit is proportional to n2.
(b) the total energy of the electron in n^th orbit is inversely proportional to n.
(c) the angular momentum of electron in an n^th orbit is an integer multiple of \(\frac{h}{2 \pi}\).
(d) the magnitude of potential energy of the electron in any orbit is greater than in kinetic energy.
Answer:
(b) the total energy of the electron in n^th orbit is inversely proportional to n.

Question 45.
Which one of the following statements is correct the X-ray beam coming from an X-ray tube will be:
(a) monochromatic
(b) having all wavelength larger than a certain maximum wavelength.
(c) having all wavelength larger than a certain minimum wavelength.
(d) having all wavelength lying between a minimum and a maximum wavelength
Answer:
(c) having all wavelength larger than a certain minimum wavelength.

Assertions and Reasons:

In each of the following questions, a statement of assertion (A) is given followed by a corresponding statement of reason (R) just below it. Of the statements, mark the correct answer is:
(a) If both assertion and reason are true and reason is the correct explanation of assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.

Question 46.
Assertion:
Nuclei having mass number about 60 are most stable.
Reason:
When two or more light nuclei are combined into a heavier nucleus, then the binding energy per nucleon will increase.
Hint:Nuclei having mass number around 60 have maximum binding energy per nucleon, so they are most stable.
Answer:
(b) If both assertion and reason are true but reason is not the correct explanation of assertion.

Question 47.
Assertion:
A beam of charged particle is employed in the treatment of cancer.
Reason:
Charged particles on passing through a material medium lose their energy by causing ionisation of the atoms along their path.
Answer:
(d) If both assertion and reason are false.

Question 48.
Assertion :
In a radioactive disintegration, an electron is emitted by the nucleus.
Reason:
Electrons are present inside the nucleus.
Hint:
Electrons are emitted as P-particles when a neutron decays into a proton during a radioactive disintegration.
Answer:
(c) If assertion is true but reason is false.

Question 49.
Assertion:
On α-decay daughter nucleus shifts two places to the left from the parent nucleus.
Reason:
An alpha particle carries four units of mass.
Hint:
An α-particle carries 2 units of positive charge. So the atomic number of the daughter nucleus decreases by 2 on α-decay.
Answer:
(b) If both assertion and reason are true but reason is not the correct explanation of assertion.

Question 50.
Assertion:
Heavy water is a better moderator than normal water.
Reason:
Heavy water absorbs neutrons more efficiently than normal water.
Hint:
Heavy water absorbs fewer neutrons than normal water. The assertion is right. The reason is false.
Answer:
(c) If assertion is true but reason is false.

Question 51.
Assertion:
Total energy of electron in an hydrogen atom is negative.
Reason:
It is bounded to the nucleus.
Answer:
(a) If both assertion and reason are true and reason is the correct explanation of assertion.

TN Board 12th Physics Important Questions