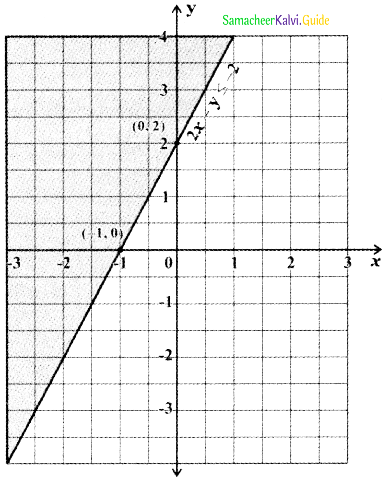
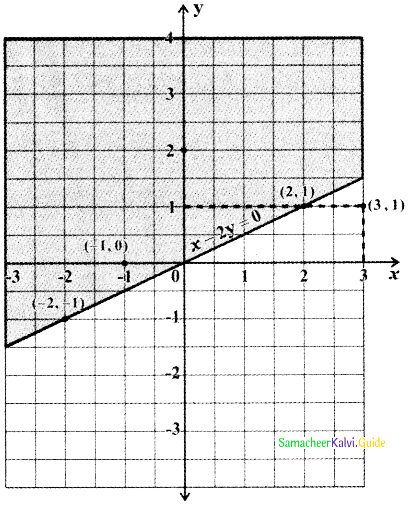
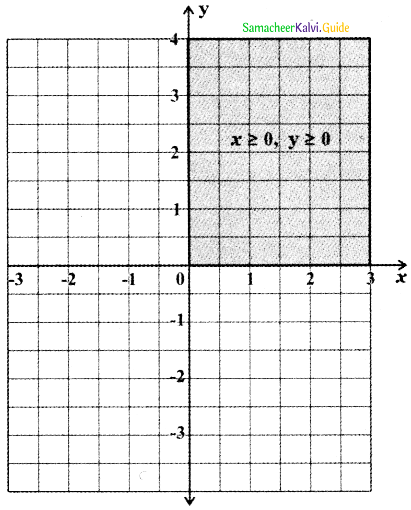
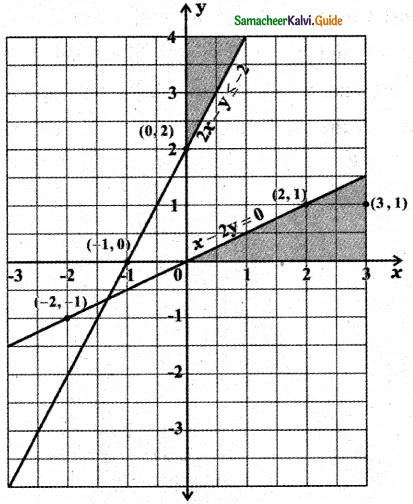
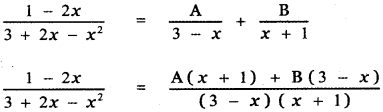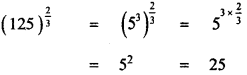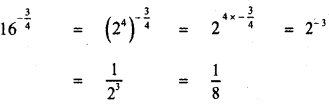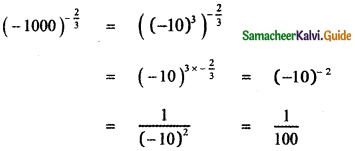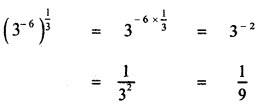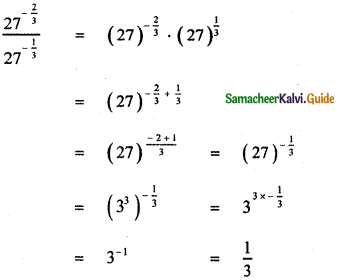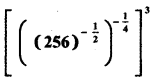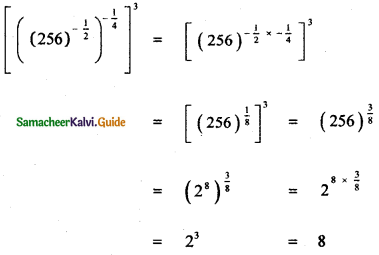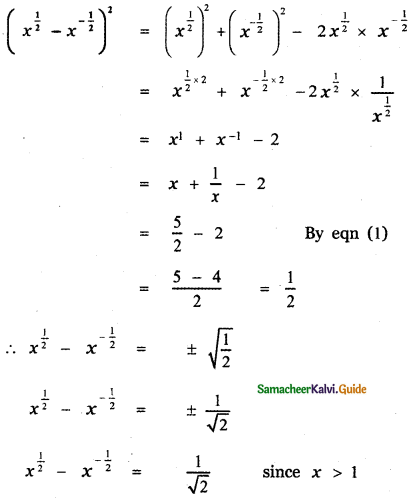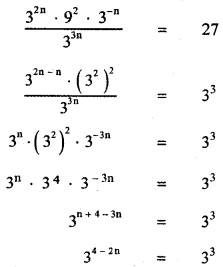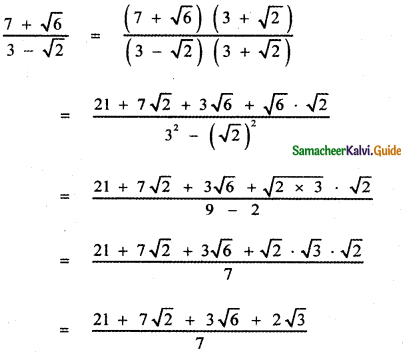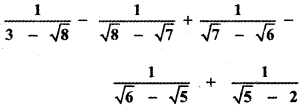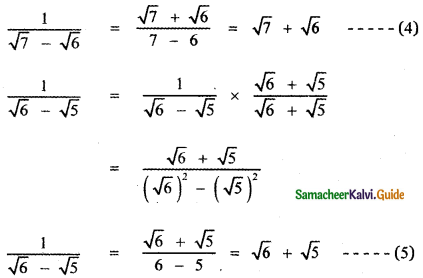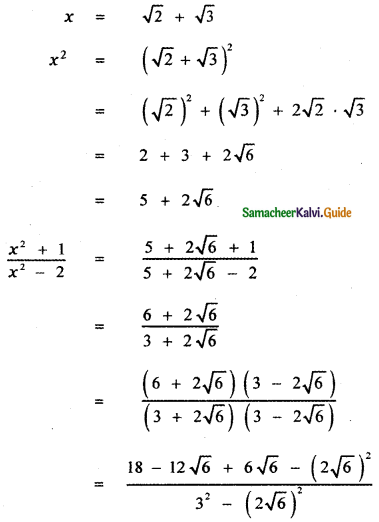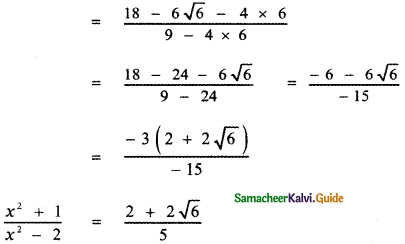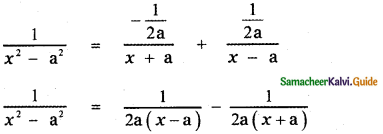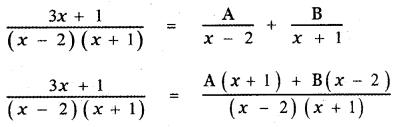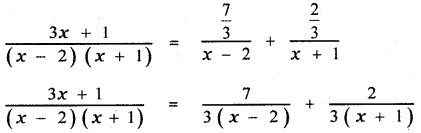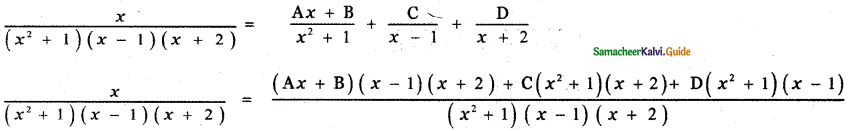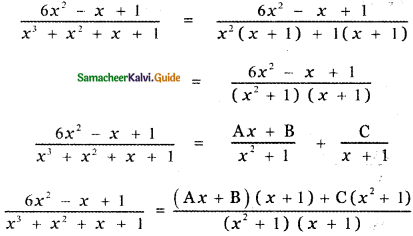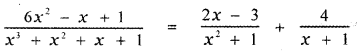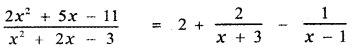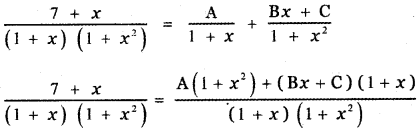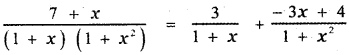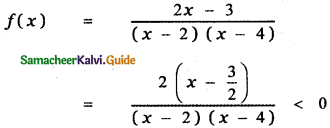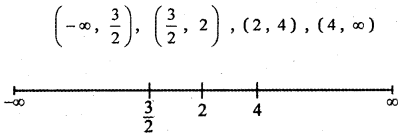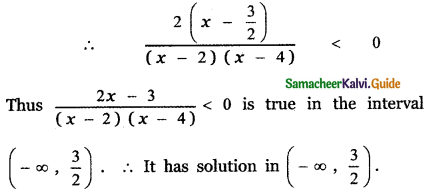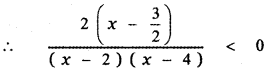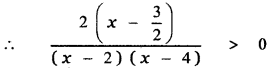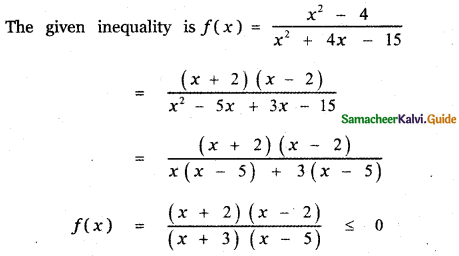Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.1
Question 1.
Identify the quadrant in which an angle of each given measure lies,
(i) 25°
(ii) 825°
(iii) – 55°
(iv) 328°
(v) – 230°
Answer:
(i) 25°
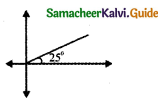
25° First quadrant
![]()
(ii) 825°
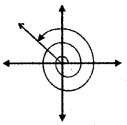
825° = 9 × 90° + 15°
825° = 2 × 360° + 105°
∴ 825° lies in the second quadrant.
iii) -55°
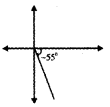
-55° lies in the fourth quadrant
iv) 328°
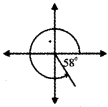
328° = 270° + 58° lies in the fourth quadrant.
v) -230°
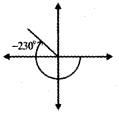
– 230° = – 180° + (- 50°) lies in the second quadrant.
![]()
Question 2.
For each given angle, find a co-terminal angle with a measure of 9 such that 0 ≤ θ < 360°.
(i) 395°
(ii) 525°
(iii) 1150°
(iv) – 270°
(v) – 450°
Answer:
(i) 395°
395° = 360° + 35°
395° – 35° = 360°
∴ Coterminal angle for 395° is 35°
(ii) 525°
525° = 360° + 165°
360° – 165° = 360°
∴Coterminal angle for 525° is 165°
(iii) 1150°
1150° = 360° + 360° + 360° + 70°
1150° = 3 × 360° + 70°
1150° – 70° = 3 × 360°
∴ Coterminal angle for 1150° is 70°.
(iv) – 270°
– 270° = 360° + 90°
– 270° – 90° = 360°
∴ Coterminal angle for -270° is 90°
(v) – 450°
– 450° = – 720° + 270°
– 450° – 270° = – 2 × 360°
∴ Coterminal angle for – 450° is 270°
![]()
Question 3.
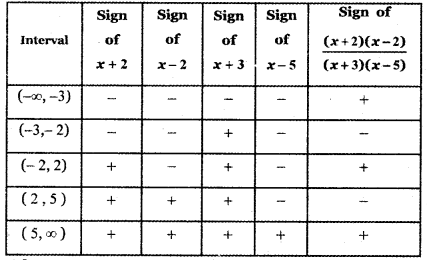
If a cos θ – b sin θ = c , show that a sin θ + b cos θ = ± \(\sqrt{\mathbf{a}^{2}+\mathbf{b}^{2}-\mathbf{c}^{2}}\)
Answer:
a cos θ – b sin θ = c
(a cos θ – b sin θ)2 + (a sin θ + b cos θ)2 = a2 cos2 θ – 2 ab sin θ cos θ + b2 sin2θ + a2 sin2 θ + b2 cos2 θ + 2 ab sin θ cos θ
c2 + (a sin 0 + b cos θ )2 = a2 cos2 θ + a2 sin2 θ + b2 sin2 θ + b2cos2θ
= a2 (cos2θ + sin2θ) + b2(sin2θ + cos2θ)
c2 + (a sin θ + b cos θ )2 = a2 + b2
(a sin θ + b cos θ)2 = a2 + b2 – c2
a sin θ + b cos θ = ± \(\sqrt{\mathbf{a}^{2}+\mathbf{b}^{2}-\mathbf{c}^{2}}\)
Question 4.
If sin θ + cos θ = m , show that cos6 θ + sin6 θ = \(\frac{4-3\left(m^{2}-1\right)^{2}}{4}\) where m2 ≤ 2.
Answer:
sin θ + cos θ = m
(sin θ + cos θ)2 = m2
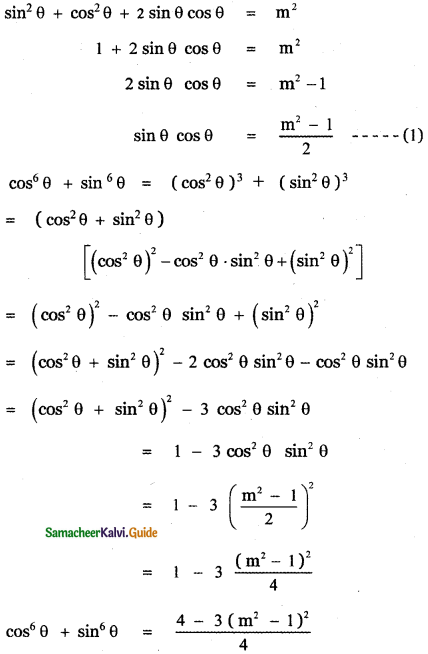
![]()
Question 5.
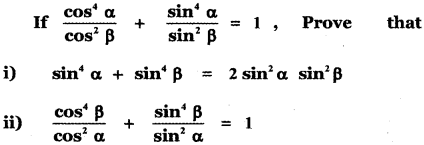
Answer:
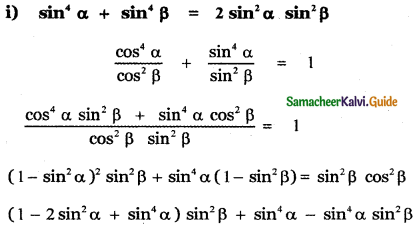
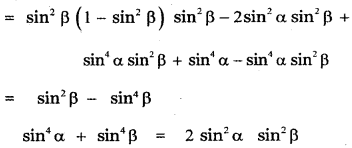
![]()
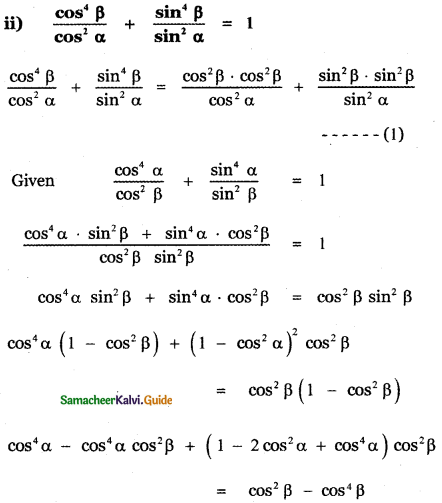

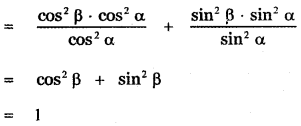
![]()
Question 6.
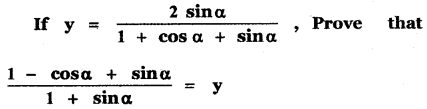
Answer:
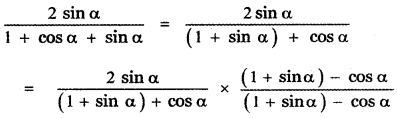

![]()
Question 7.

Answer:

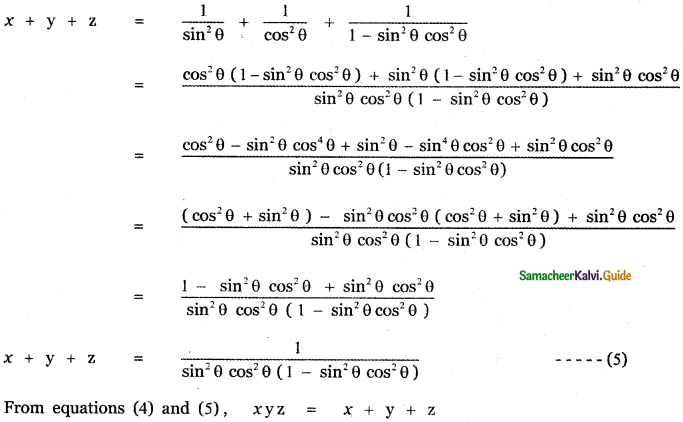
![]()
Question 8.
If tan2 θ = 1 – k2, show that sec θ + tan3 θ cosec θ = ( 2 – k2)3/2. Also, find the values of k for which this result holds.
Answer:
tan2 θ = 1 – k2
1 + tan2 θ = 1 + 1 – k2
sec2θ = (2 – k2)
sec2θ = (2 – k2)1/2
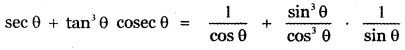

tan2 θ = 1 – k2
When θ = \(\frac{\pi}{2}\), tan \(\frac{\pi}{2}\) = ∞, not defined 2
When θ = 0, tan2 0 = 1 – k2
1 – k2 = 0 ⇒ k2 = 1 ⇒ k = ± 1
When θ = 45°, tan2 45° = 1 – k2
1 – k2 = 1 ⇒ – k2 = 0 ⇒ k = 0
When θ > 45°, say θ = 60°
tan2 60° = 1 – k2 = (√3)2 = 1 – k2
3 = 1 – k2 ⇒ k2 = 1 – 3 = – 2
∴ θ > 45°, k2 is negative ⇒ k is imaginary
∴ k lies between -1 and 1 ⇒ k ∈ [-1 , 1]
![]()
Question 9.
If sec θ + tan θ = p, obtain the values of sec θ, tan θ and sin θ in terms of p.
Answer:
Given sec θ + tan θ = p
We have sec2 θ – tan2 θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
p (sec θ – tan θ) = 1
sec θ – tan θ = \(\frac{1}{p}\)
(sec θ – tan θ) + (sec θ – tan θ) = p + \(\frac{1}{p}\)

![]()
Question 10.
If cot θ(1 + sin θ) = 4m and cot θ (1 – sin θ) = 4n then prove that (m2 – n2)2 = mn.
Answer:
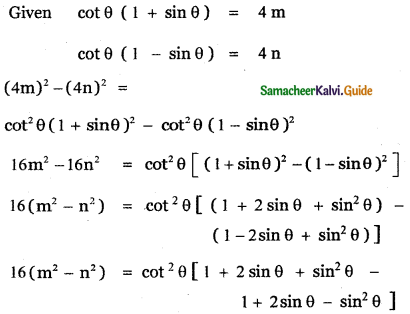
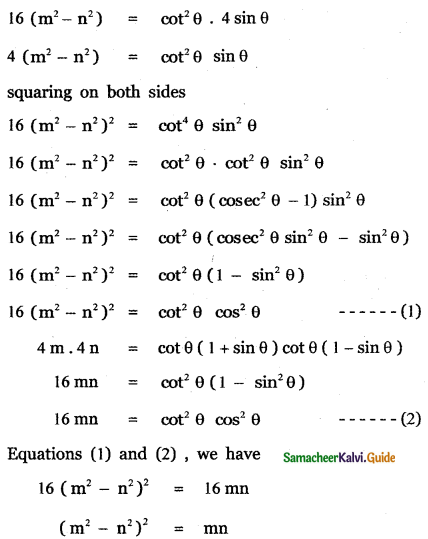
![]()
Question 11.
If cosec θ – sin θ = a3, sec θ – cos θ = b3 then prove that a2b2(a2 + b2) = 1.
Answer:


![]()
Question 12.
Eliminate θ from the equations a sec θ – c tan θ = b, b sec θ + d tan θ = c.
Answer:
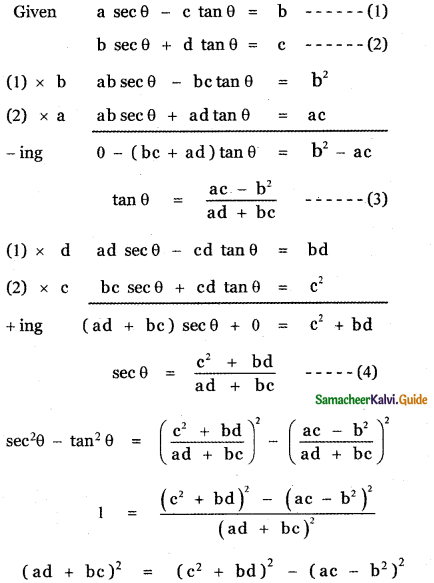
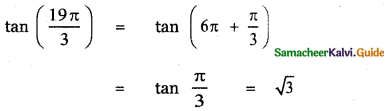
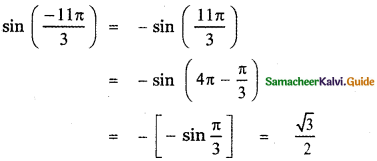
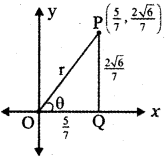
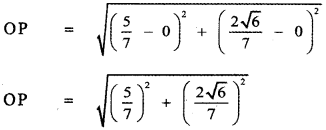

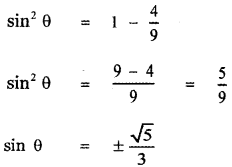
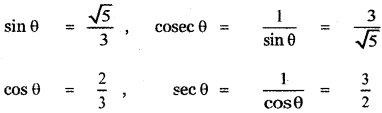
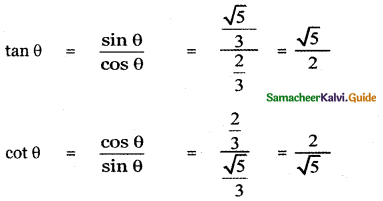
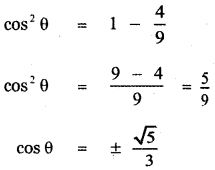
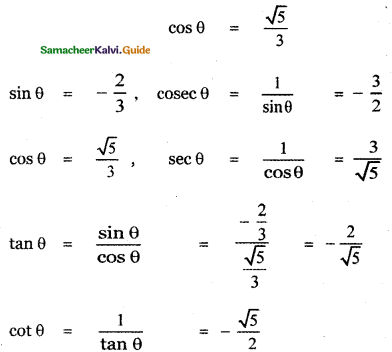

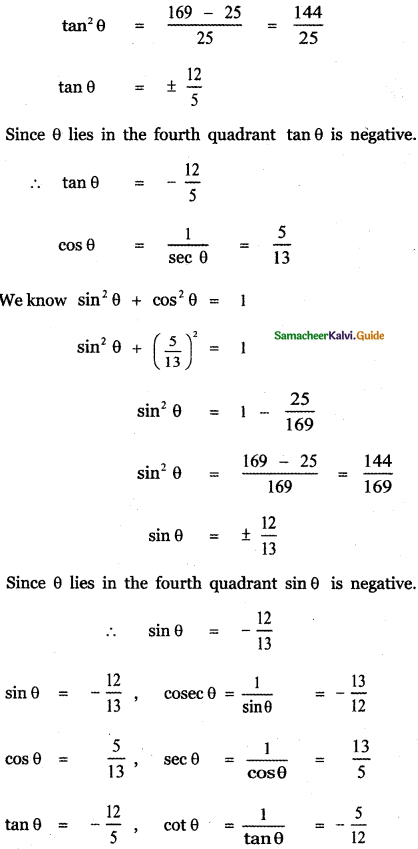


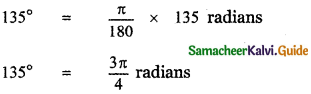




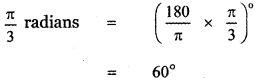




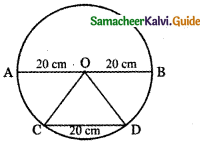
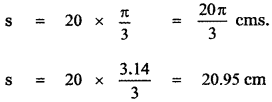

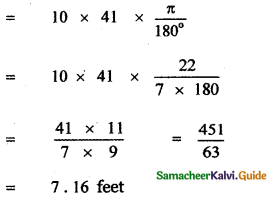

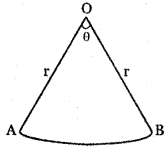

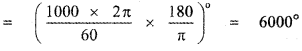


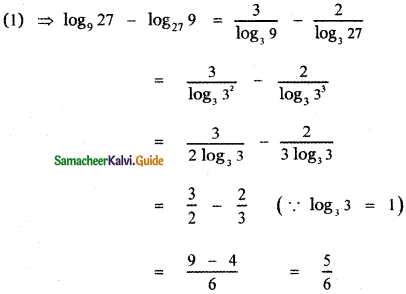

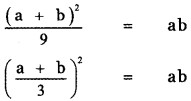
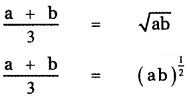
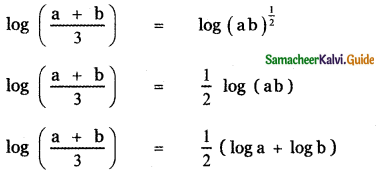
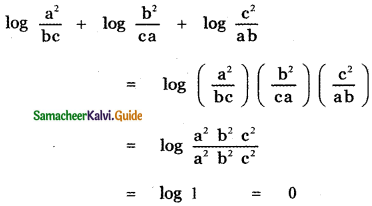
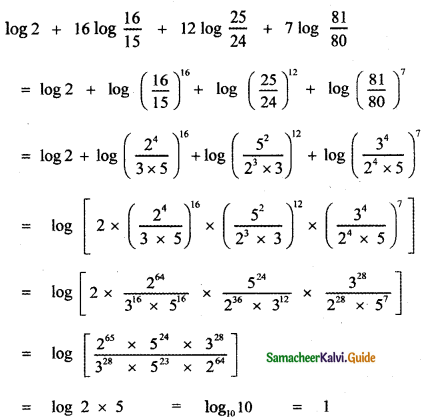
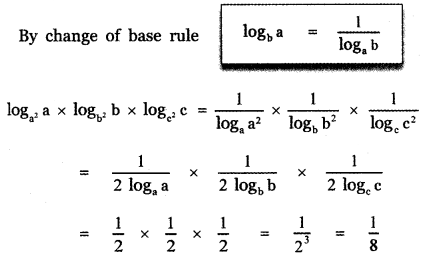
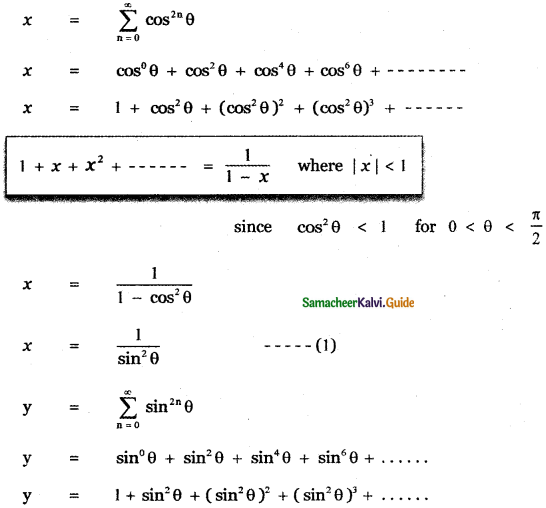
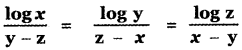 , then prove that xyz = 1
, then prove that xyz = 1

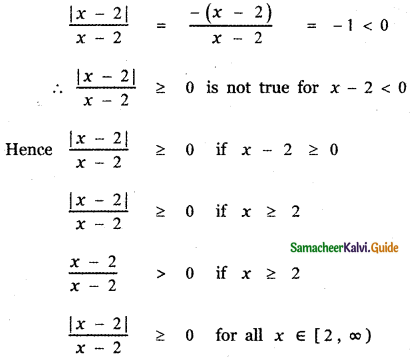
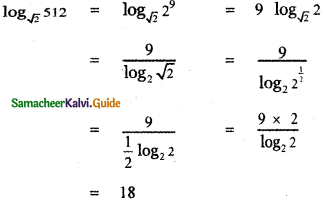
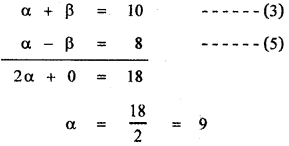
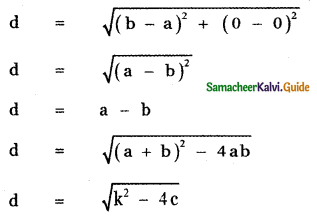
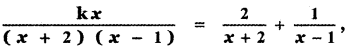 then the value of k is
then the value of k is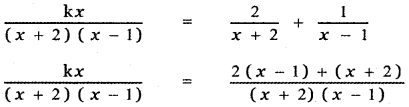
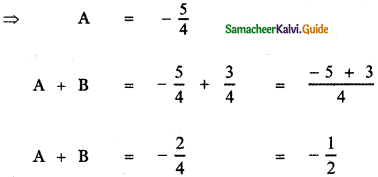
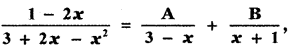 , then the value of A + B is
, then the value of A + B is