Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.10 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.10
Determine the region in the plane determined by the inequalities
Question 1.
x ≤ 3y, x ≥ y
Answer:
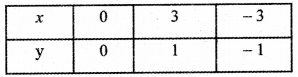
Consider the line x = 3y
When y = 0 ⇒ x = 0
When y = 1 ⇒ x = 3
When y = – 1 ⇒ x = – 3
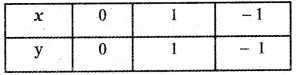
Consider the line x = y
When x = 0 ⇒ y = o
When x = 1 ⇒ y = 1
When x = – 1 ⇒ y = – 1
![]()
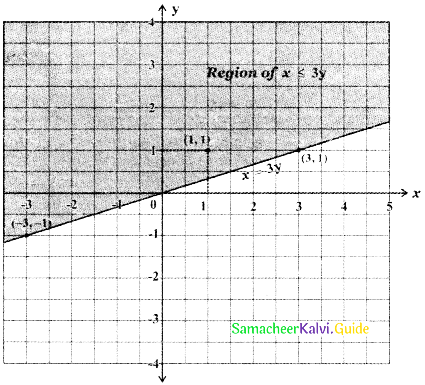
To find the region of x ≤ 3y: The line x = 3y divides the cartesian plane into two half planes. Consider the point (1,1) this point satisfies the inequality x < 3y. This point (1,1) lies above the line x = 3y.
Hence all points satisfying the inequality lie above the line x = 3y.
Therefore x < 3y represents the upper half plane of the Cartesian plane bounded by the line x = 3y. Since x ≤ 3y, this region also contains all the points on the straight line x = 3y.
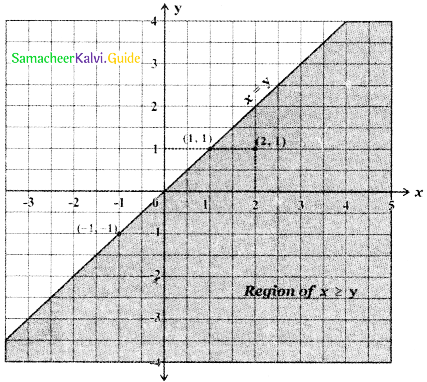
To find the region x ≥ y: The line x = y divides the cartesian plane into two half planes. Consider the point (2,1). This point (2,1) satisfies the inequality x > y and this point (2,1) lies below the line x = y. ∴ All points satisfying the inequality x > y will lie below the line x = y. Therefore x > y represents the lower half plane of the cartesian plane bounded by the line x = y. Since x > y this region also contains all the points on the straight line x = y.
The required region is the region common to the regions x ≤ 3y and x ≥ y
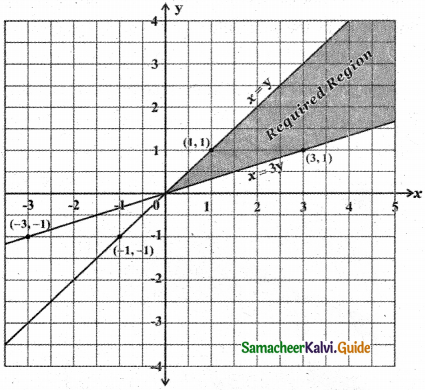
![]()
Question 2.
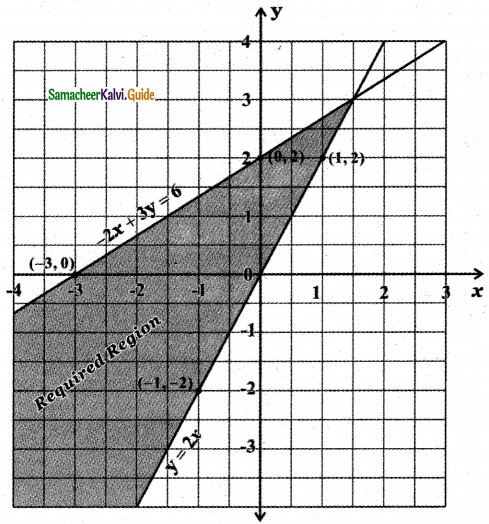
y ≥ 2x, – 2x + 3y ≤ 6
Answer:
Consider the straight line y = 2x
When x = 0 ⇒ y = 2 × 0 = 0
When x = 0 ⇒ y = 2 × 1 = 2
When x = – 1 ⇒ y = 2 × – 1 = – 2

Consider the line – 2x + 3y = 6
When x = 0 ⇒ – 2 × 0 + 3y = 6 ⇒ 3y = 6 ⇒ y = 2
When y = 0 ⇒ – 2x + 3 × 0 = 6 ⇒ -2x = 6 ⇒ x = – 3
To find the region of y ≥ 2x: The straight line y = 2x divides the cartesian plane into two half planes. Consider the point (1, 3) satisfying the inequality y > 2x. This point (1, 3) lies above the straight line y = 2x. ∴ All points satisfying the inequality y > 2x will lie above the line y = 2x.
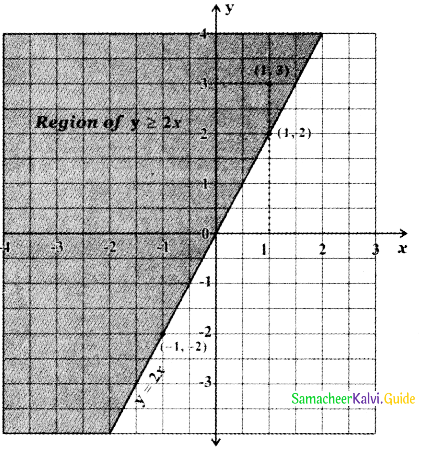
![]()
To find the region of -2x + 3y ≤ 6:
The straight line – 2x + 3y = 6 divides the cartesian plane into two half planes one half plane contains the origin and the other half plane does not contain the origin.
Substitute the origin (0, 0) in the inequality – 2x + 3y < 6
we get – 2 × 0 + 3 × 0 < 6 ⇒ 0 < 6
∴ (0,0) satisfies the inequality – 2x + 3y < 6
∴ The inequality – 2x + 3y < 6 represents the half plane containing the origin. Since – 2x + 3y ≤ 6, this region contains all the points on the straight line – 2x + 3y = 6.
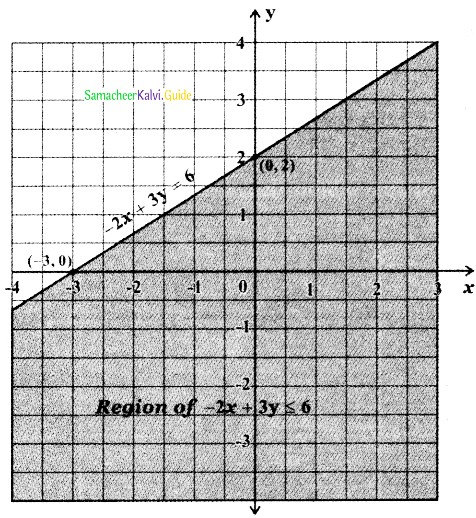
The required region is the region common to y ≥ 2x and – 2x + 3y ≤ 6
![]()
Question 3.
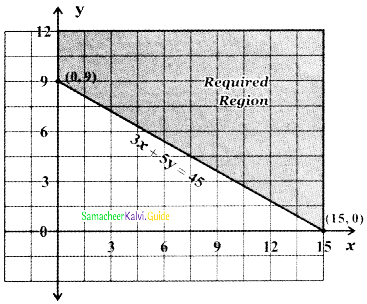
3x + 5y ≥ 45, x ≥ 0, y ≥ 0
Answer:
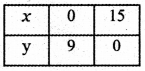
Consider the line 3x + 5y = 45
when x = 0, 3 × 0 + 5y = 45 ⇒ y = \(\frac{45}{5}\) = 9
when y = 0, 3x + 5 × 0 = 45 ⇒ x = \(\frac{45}{3}\) = 15
To find the region of x ≥ 0, y ≥ 0:
x ≥ 0 and y ≥ 0 denote the first quadrant of the Cartesian plane.
Since x ≥ 0 and y ≥ 0 this region contains all the points on the lines x = 0 and y = 0.
To find the region of 3x + 5y ≥ 45: The straight-line 3x + 5y = 45 divides the cartesian plane into two half-planes, one-half plane containing the origin and the other half-plane does not contain the origin.
Substitute the origin (0,0) in the inequality 3x + 5y > 45 we get 3 × 0 + 5 × 0 > 45 ⇒ 0 > 45 which is impossible. Therefore, (0, 0) does not satisfy the inequality 3x + 5y > 45 represents the half plane that does not contain the origin bounded by the straight line 3x + 5y = 45. Since 3x + 5y ≥ 45, x ≥ 0, y ≥ 0, this region contains all the points on the straight lines 3x + 5y = 45.
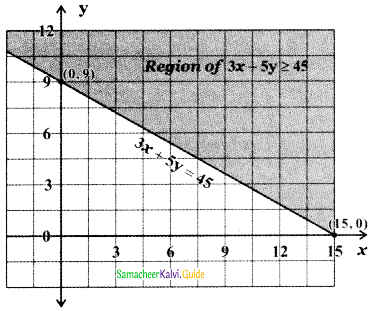
∴ The required region is the common region bounded by x ≥ 0, y ≥ 0, and 3x + 5y ≥ 45.
![]()
Question 4.
2x + 3y ≤ 35, y ≥ 2, x ≥ 5.
Answer:
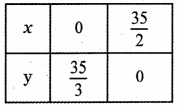
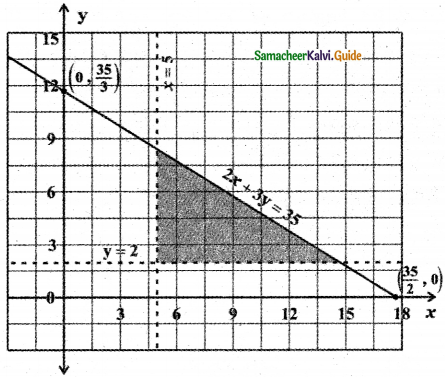
Consider the straight line 2x + 3y = 35
When x = 0, 2 × 0 + 3y = 35 ⇒ \(\frac{35}{3}\)
When y = 0, 2x + 3 × 0 = 35 ⇒ \(\frac{35}{2}\)
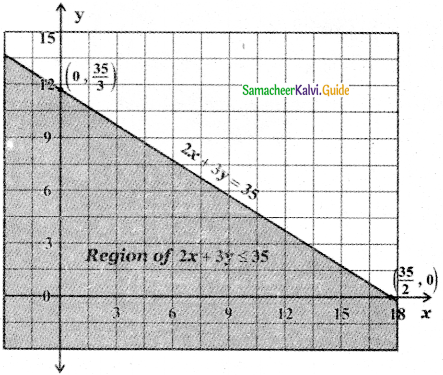
To find the region of 2x + 3y ≤ 35: The straight-line 2x + 3y = 35 divides the cartesian plane into two half-planes, one-half plane contains the origin and the other half-plane does not contain the origin.
Substitute the origin (0, 0) in the inequality 2x + 3y < 35, we get 2 × 0 + 3 × 0 < 35 ⇒ 0 < 35. (0, 0) satisfies the inequality.
Therefore, the inequality 2x + 3y < 35 represents the half plane that contains the origin (0, 0) bounded by the straight line 2x + 3y = 35. Since 2x + 3y ≤ 35, this region contains all the points on the straight line 2x + 3y = 35.
![]()
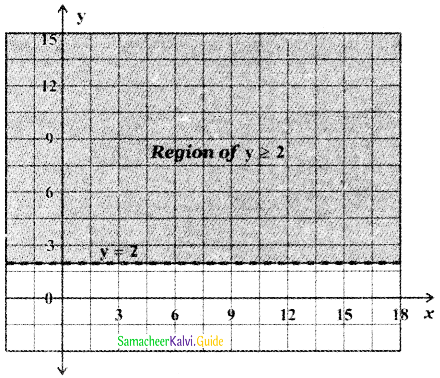
To find the region y ≥ 2: The straight line y = 2 divides the cartesian plane into two half-planes, one-half plane contains the origin and the other half-plane does not contain the origin. Substitute the point (0, 0) in the inequality y ≥ 2 we get 0 >2 which is impossible. Hence (0, 0) does not satisfy the inequality y > 2.
∴ The inequality y > 2 represents the half-plane that does not contain the origin bounded by the straight line y = 2. Since y ≥ 2, this region contains all the points on the straight line y = 2.
To find the region x ≥ 5: The straight line x – 5 divides the cartesian plane into two half-planes, one half-plane containing the origin and the other half-plane does not contain the origin.
Substitute the origin (0,0) in the inequality x > 5 we get 0 > 5 which is impossible. Hence (0, 0) does not satisfy the inequality x > 5.
∴ The inequality x > 5 represents the half-plane that does not contain the origin bounded the straight line x = 5.
Since x ≥ 5, this region contains all the points on the straight line x = 5
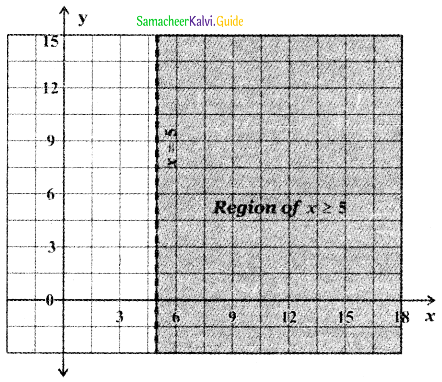
∴ The required region is the common region bounded by 2x + 3y ≤ 35, y ≥ 2, x ≥ 5.
![]()
Question 5.
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Answer:
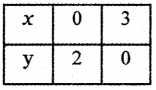
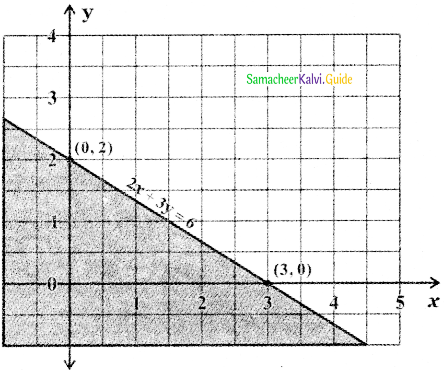
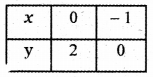
Consider the straight line 2x + 3y = 6
When x = 0, 2 × 0 + 3y = 6 ⇒ y = \(\frac{6}{3}\) = 2
When y = 0, 2x + 3 × 0 = 6 ⇒ x = \(\frac{6}{2}\) = 3
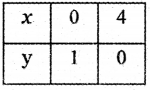
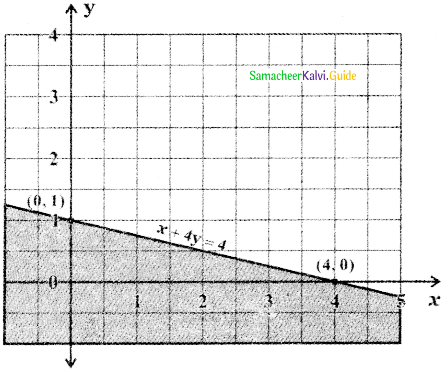
Consider the straight line x + 4y = 4
When x = 0 ⇒ 0 + 4y = 4 ⇒ y = \(\frac{4}{4}\) = 1
When y = 0 ⇒ x + 4 × 0 = 4 ⇒ x = 4
To find the region of 2x + 3y ≤ 6: The straight line 2x + 3y = 6 divides the cartesian plane into two half planes, one half plane contains the origin and the other half plane does not contain the origin. Substitute the origin (0, 0) in the inequality 2x + 3y < 6 we get 2 × 0 + 3 × 0 < 6 ⇒ 0 < 6
∴ The origin (0,0) satisfies the inequality 2x + 3y < 6. Hence the inequality 2x + 3y < 6 represents the half plane that contains the origin (0, 0). Since 2x + 3y ≤ 6, this region contains all the points on the straight line 2x + 3y = 6.
![]()
To find the region of x + 4y ≤ 4 : The straight line x + 4y = 4 divides the cartesian plane into two half planes, one half plane contains the origin and the other half plane does not contain the origin. Substitute the origin (0, 0) in the inequality x + 4y < 4, we get 0 + 4 × 0 < 4 ⇒ 0 < 4.
Therefore the origin (0, 0) satisfies the inequality x + 4y < 4. Therefore the inequality x + 4y < 4 represents the half-plane that contains the origin bounded by the line x + 4y = 4. Since x + 4y ≤ 4, this region contains all the points on the straight line.
To find the region x ≥ 0, y ≥ 0: x ≥ 0 and y ≥ 0 denote the first quadrant of the cartesian plane.
Since x ≥ 0 and y ≥ 0 this region contains all the points on the lines x = 0 and y = 0.
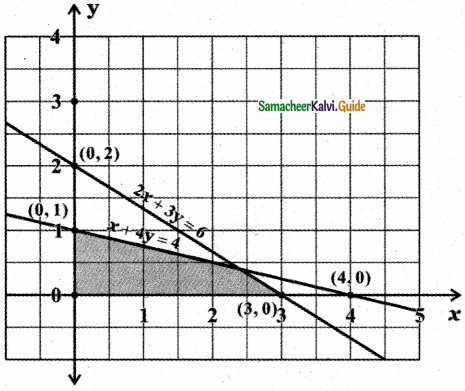
The required region is the common region bounded by 2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0 and y ≥ 0.
![]()
Question 6.
x – 2y ≥ 0 , 2x – y ≤ – 2 , x ≥ 0, y ≥ 0
Answer:
Consider the straight line x – 2y = 0
When x = 0
⇒ -2y = 0
⇒ y = 0
When x = 2
⇒ 2 – 2y = 0
⇒ 2y = 2
⇒ y = 1
When x = -2
⇒ – 2 – 2y = 0
⇒ -2y = 2
⇒ y = – 1

Consider the line 2x – y = – 2
When x = 0 ⇒ – y = – 2 ⇒ y = 2
When y = 0 ⇒ 2x – 0 = – 2 ⇒ x = – 1
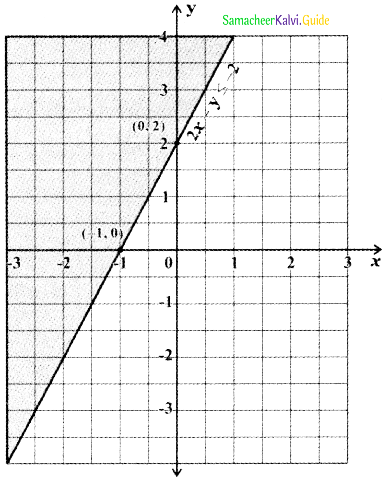
To find the region of x – 2y ≥ 0: The straight line x – 2y = 0 divides the cartesian plane into two half-planes. Consider the point (3,1) satisfying the inequality x > 2y. The point (3, 1) lies below the straight line x = 2y in the cartesian plane.
∴ All the points satisfying the inequality x > 2y will lie in the half-plane below the straight line x = 2y. Since x ≥ 2y this region contains all the points on the straight line x = 2y.
![]()
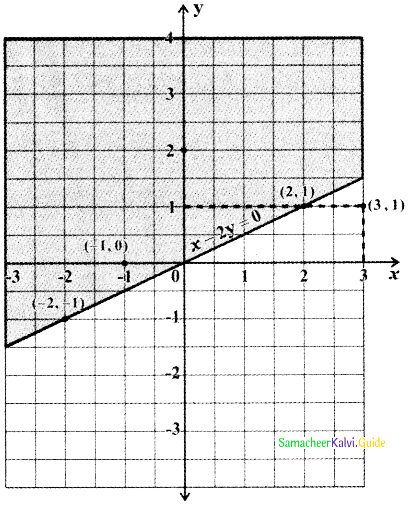
To find the region of 2x – y ≤ – 2:
-(2x – y) ≥ 2 ⇒ – 2x + y ≥ 2
Consider the straight line – 2x + y = 2. This line divides the cartesian plane in to two half planes, one half plane contains the origin and the other half plane does not contain the origin. Substitute the origin (0, 0) in the inequality – 2x + y > 2 we get- 2 × 0 + 0 > 2 ⇒ 0 > 2 which is impossible. Therefore (0, 0) does not satisfy the inequality -2x + y > 2. Hence the inequality -2x + y > 2 represents the half plane that does not contain the origin bounded by the straight line. Since -2x + y > 2, this region contains all the points on the straight line -2x + y = 2
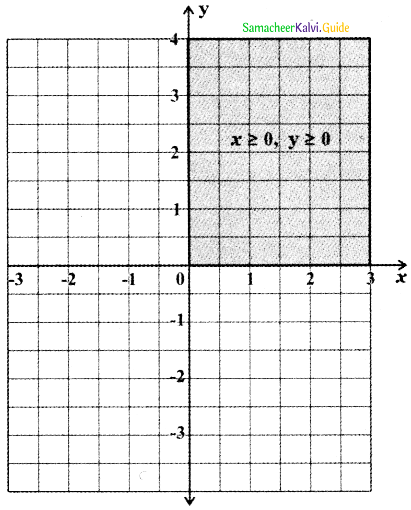
To find the region of x ≥ 0, y ≥ 0: x ≥ 0 and y ≥ 0 denote the first quadrant of the cartesian plane. Since x ≥ 0 and y ≥ 0 this region contains all the points on the lines x = 0 and y = 0.
∴ The required region is the region common to x – 2y ≥ 0 , 2x – y ≤ – 2 , x ≥ 0, y ≥ 0.
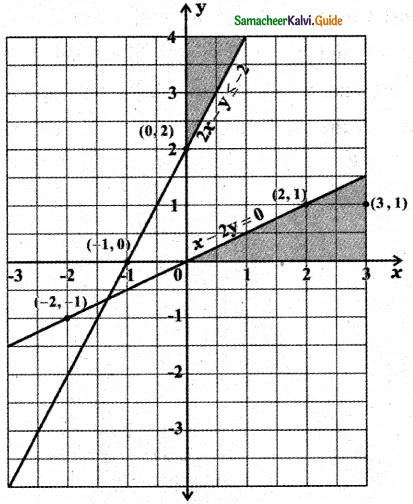
![]()
Question 7.
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
Answer:
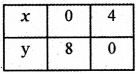
Consider the straight line 2x + y = 8
When x = 0 ⇒ 2 × 0 + y = 8 ⇒ y = 8
When y = 0 ⇒ 2x + 0 = 8 ⇒ x = \(\frac{8}{2}\) = 4
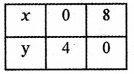
Consider the straight line x + 2y = 8
When x = 0 ⇒ 0 + 2y = 8 ⇒ y = \(\frac{8}{2}\) = 4
When y = 0 ⇒ x + 2 × 0 = 8 ⇒ x = 8
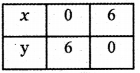
Consider the straight line x + y = 6
When x = 0 ⇒ 0 + y = 6 ⇒ y = 6
When y = 0 ⇒ x + 0 = 6 ⇒ x = 6
![]()
To find the region of 2x + y ≥ 8: The straight-line 2x + y = 8 divides the cartesian plane into two half-planes one half plane contains the origin and the other half plane does not contain the origin. Substitute the origin (0, 0) in the inequality 2x + y > 8 we get 2 × 0 + 0 > 8 ⇒ 0 > 8 which is impossible.
∴ The origin (0, 0) does not satisfy the inequality 2x + y > 8. Hence the inequality 2x + y > 8 represents the half plane that does not contain the origin bounded by the straight line 2x + y = 8. Since 2x + y ≥ 8, this region contains all the points on the straight line 2x + y = 8.
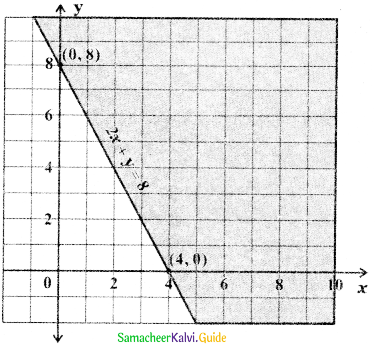
To find the region of x + 2y ≥ 8: The straight line x + 2y = 8 divides the cartesian plane into two half planes, one half plane contains the origin and the other half plane doesnot contain the origin. Substitute the origin (0, 0) in the inequality x + 2y > 8 we get 0 + 2 × 0 > 8 ⇒ 0 > 8 which is impossible. ∴ The origin (0, 0) does not satisfy the inequality x + 2y > 8. Therefore, the inequality x + 2y > 8 represents the half plane that does not contain the origin bounded by the straight line x + 2y = 8. Since x + 2y ≥ 8 this region contains all the points on the straight line x + 2y = 8.
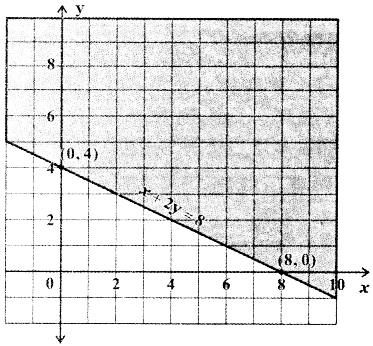
To find the region of x + y ≤ 6: The straight line x + y = 6 divides the cartesian plane into two half-planes, one half-plane contains the origin and the other half-plane does not contain the origin. Substitute the origin (0, 0) in the inequality x + y < 6 we get 0 + 0 < 6 ⇒ 0 < 6 which is true.
∴ The origin (0, 0) satisfies the inequality x + y < 6. Hence, the inequality x + y < 6 represents the half plane that contains the origin bounded by the straight line x + y = 6. Since x + y ≤ 6, this region contains all the points on the straight line x + y = 6.
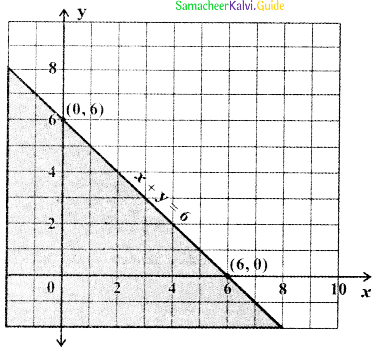
Thus the required region is the region common to 2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
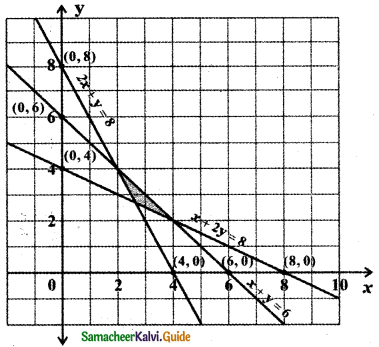
![]()