Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.13 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.13
Question 1.
If |x + 2| ≤ 9 then x belongs to
(1) (- ∞,- 7)
(2) [- 11, 7]
(3) (-∞, – 7) ∪ [11, ∞]
(4) (-11, 7)
Answer:
(2) [- 11, 7]
![]()
Explanation:
-x – 2 ≤ 9 x + 2 ≤ 9
-x < 9 + 2 = 11 x ≤ 9 – 2 = 7
⇒ x ≥ -11
so x ∈ [-11, 7]
Question 2.
Given that x, y and b are real numbers x < y, b > 0 then
(1) xb < yb
(2) xb > yb
(3) xb < yb
(4) \(\frac{x}{b}\) ≥ \(\frac{y}{b}\)
Answer:
(1) xb < yb
Explanation:
Given x, y and b are real numbers and b ≥ 0. x > b
Multiplying by positive real number the inequality is not affected.
∴ xb < yb
![]()
Question 3.
If \(\frac{|x-2|}{x-2}\) ≥ 0 , then x belongs to
(1) [2, ∞)
(2) (2, ∞)
(3) (-∞, 2)
(4) (-2, ∞)
Answer:
(1) [2, ∞)
Explanation:
Given \(\frac{|x-2|}{x-2}\) ≥ 0
By the definition of mod function
|x – 2 | = – (x – 2) if x – 2 < 0 | x – 2 | = x – 2 if x – 2 > 0
Suppose x – 2 < 0 then
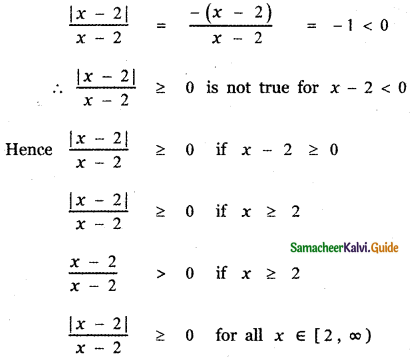
![]()
Question 4.
The solution of 5x – 1 < 24 and 5x + 1 > – 24 is
(1) (4, 5)
(2) (- 5, – 4)
(3) (- 5, 5)
(4) (- 5, 4)
Answer:
(3) (- 5, 5)
Explanation:
The given inequalities are
5x – 1 < 24 ——— (1)
5x + 1 > – 24 ——– (2)
(1) ⇒ 5x – 1 < 24
⇒ 5x < 24 + 1
⇒ 5x < 25 ⇒ x < 5 ——— (3)
(2) ⇒ 5x + 1 > – 24
⇒ 5x > – 24 – 1
⇒ 5x > – 25
⇒ x > – 5 ——– (4)
Combining (3) and (4), we have
-5 < x < 5
∴ x ∈ (- 5, 5)
![]()
Question 5.
The solution set of the following inequality
|x – 1| ≥ |x – 3| is
(1) [0, 2]
(2) [2, ∞)
(3) (0, 2)
(4) (-∞, 2)
Answer:
(2) [2, ∞)
Explanation:
The given inequality is |x – 1| ≥ |x – 3|
(x – 1)2 ≥ (x – 3)2
x2 – 2x + 1 ≥ x2 – 6x + 9
– 2x + 1 ≥ – 6x + 9
6x – 2x + 1 – 9 ≥ 0
4x – 8 ≥ 0 ⇒ 4x ≥ 8
⇒ x ≥ 2
∴ The solution set of the given inequality lies in the interval (2, ∞)
![]()
Question 6.
The value of \(\log _{\sqrt{2}} 512\) is
(1) 16
(2) 18
(3) 9
(4) 12
Answer:
(2) 18
Explanation:
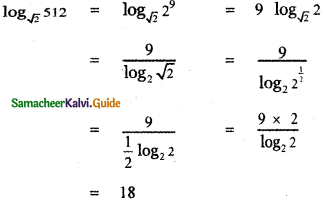
![]()
Question 7.
The value of \(\log _{3} \frac{1}{81}\) is
(1) – 2
(2) – 8
(3) – 4
(4) – 9
Answer:
(3) – 4
Explanation:
\(\log _{3} \frac{1}{81}\) = log31 – log381
= o – log3 34
= – 4 log33
= – 4 × 1
= – 4
Question 8.
If log√x0.25 = 4, then the value of x is
(1) 0.5
(2) 2.5
(3) 1.5
(4) 1.25
Answer:
(1) 0.5
Explanation:
log√x0.25 = 4
By the definition of logarithm
0.25 = \((\sqrt{x})^{4}\)
(0.5 )2 = \(\left(x^{\frac{1}{2}}\right)^{4}\)
(0.5 )2 = x2
x = 0.5
![]()
Question 9.
The value of logab . logbc . logca is
(1) 2
(2) 1
(3) 3
(4) 4
Answer:
(2) 1
Explanation:
logab . logbc . logca = logac . logca
= logaa = 1
Question 10.
If 3 is the logarithm of 343 then, the base is
(1) 5
(2) 7
(3) 6
(4) 9
Answer:
(2) 7
Explanation:
⇒ logx343 = 3 ⇒ 343 = x3
(.i.e.,) 73 = x3 ⇒ x = 7
⇒ x = 7
![]()
Question 11.
Find a so that the sum and product of the roots of the equation 2x2 + (a – 3 ) x + 3a – 5 = 0 are equal is
(1) 1
(2) 2
(3) 0
(4) 4
Answer:
(2) 2
Explanation:
Given quadratic equation is
2x2 + (a – 3) x + 3a – 5 = 0
Let the roots be α, β
Sum of the roots α + β = \(-\frac{(a-3)}{2}\)
Product of the roots α β = \(\frac{3 a-5}{2}\)
Given α + β = α β
∴ \(-\frac{(a-3)}{2}=\frac{3 a-5}{2}\)
– a + 3 = 3a – 5
3a + a = 5 + 3
4a = 8 ⇒ a = 2
![]()
Question 12.
If a and b are the roots of the equation x2 – kx +16 = 0 and satisfy a2 + b2 = 32, then the value of k is
(1) 10
(2) – 8
(3) – 8, 8
(4) 6
Answer:
(3) – 8, 8
Explanation:
a + b = k ….(1) ab = 16 ….(2)
a2 + b2 = (a + b)2 – 2ab = 32 .
k2 – 32 = 32 ⇒ k2 = 64 ⇒ k = ±8
![]()
Question 13.
The number of solutions of x2 + |x – 1| = 1 is
(1) 1
(2) 0
(3) 2
(4) 3
Answer:
(3) 2
Explanation:
The given quadratic equatiuon is
x2 + |x – 1| = 1 ——– (1)
Case(i)
By the definition of mod function if x – 1 ≥ 0, then
|x – 1| = x – 1
∴ (1) ⇒ x2 + x – 1 = 1
x2 + x – 2 = 0
x2 + 2x – x – 2 = 0
x(x + 2) – 1 (x + 2) = 0
(x – 1)(x + 2) = 0
x – 1 = 0 or x + 2 = 0
x = 1 or x = – 2
Since x – 1 ≥ 0
x = – 2 is not possible. ∴ x = 1
Case (ii)
Again by the definition of mod function if x – 1 < 0 then
|x – 1| = – (x – 1)
∴ (1) ⇒ x2 – (x – 1) = 1
x2 – x + 1 = 1
x2 – x = 0
x (x – 1 ) = 0
x = 0 or x – 1 = 0
x = 0 or x = 1
Since x < 1, x = 1 is not possible
∴ x = 0
∴ The required solution set is {0, 1}
Number of solutions = 2
![]()
Question 14.
The equation whose roots are numerically equal but opposite in sign to the roots of 3x2 – 5x – 7 = 0 is
(1) 3x2 – 5x – 7 = 0
(2) 3x2 + 5x – 7 = 0
(3) 3x2 – 5x + 7 = 0
(4) 3x2 + x – 7 = 0
Answer:
(2) 3x2 + 5x – 7 = 0
Explanation:
The given quadratic equation is
3x2 – 5x – 7 = 0 ——— (1)
Let α and β be the roots of eqn (1)
Sum of the roots α + β = \(-\left(\frac{-5}{3}\right)\)
α + β = \(\frac{5}{3}\)
Product of the roots α β = – \(\frac{7}{3}\)
The quadratic equation whose roots are – α and – β is
x2 – (sum of the roots) x + Product of the roots = 0
x2 – (- α – β)x + (- α)(- β) = 0
x2 + (α + β)x + αβ = 0
x2 + \(\frac{5}{3}\) x – \(\frac{7}{3}\) = 0
3x2 + 5x – 7 = 0 is the required equation.
![]()
Question 15.
If 8 and 2 are the roots of x2 + ax + c = 0 and 3, 3 are the roots of x2 + dx + b = 0 , then the roots of the equation x2 + ax + b = 0 are
(1) 1, 2
(2) -1, 1
(3) 9, 1
(4) -1, 2
Answer:
(3) 9, 1
Explanation:
Given that 8 and 2 are the roots of the equation
x2 + ax + c = 0 ———- (1)
Sum of the roots 8 + 2 = \(-\frac{a}{1}\) ⇒ a = -10
Product of the roots 8 × 2 = \(\frac{c}{1}\) ⇒ c = 16
Also given 3 , 3 are the roots of
x2 + dx + b = 0 ——— (2)
Sum of the roots 3 + 3 = – \(\frac{d}{1}\) ⇒ d = – 6
Product of the roots 3 × 3 = \(\frac{b}{1}\) ⇒ b = 9
Let a and p be roots of the equation x2 + ax + b = 0
Sum of the roots α + β = – y
α + β = -(-10)
α + β = 10 ——– (3)
Product of the roots α β = y
α β = 9 ———- (4)
(α – β) = (α + β)2 – 4αβ
= 102 – 4 × 9
= 100 – 36 = 64
α – β = 8 ——— (5)
Solving equations (3) and (5)
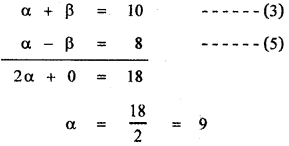
Substituting in equation (3),
9 + β = 10
⇒ β = 10 – 9 = 1
∴ The required roots are 9, 1
![]()
Question 16.
If a and b are the real roots of the equation x2 – kx + c = 0 , then the distance between the
points(a, 0) and (b, 0)is
(1) \(\sqrt{\mathbf{k}^{2}-4 \mathbf{c}}\)
(2) \(\sqrt{4 k^{2}-c}\)
(3) \(\sqrt{4 \mathbf{c}-\mathbf{k}^{2}}\)
(4) \(\sqrt{\mathbf{k}-8 \mathbf{c}}\)
Answer:
(1) \(\sqrt{\mathbf{k}^{2}-4 \mathbf{c}}\)
Explanation:
Given that a and b are the roots of the equation
x2 – kx + c = 0 ——— (1)
Sum of the roots a + b = \(-\frac{(-k)}{1}\)
a + b = k ———- (2)
Product of the roots ab = \(\frac{c}{1}\)
ab = c ——– (3)
Distance between the points ( a, 0) and (b, 0) is
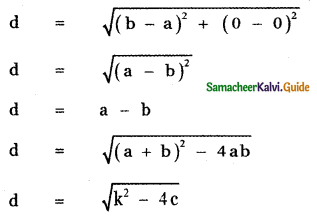
![]()
Question 17.
If 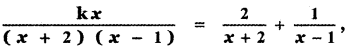 then the value of k is
then the value of k is
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(3) 3
Explanation:
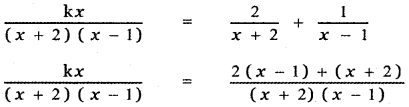
kx = 2x – 2 + x + 2
kx = 3x ⇒ k = 3
Question 18.
If 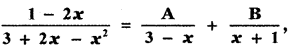 , then the value of A + B is
, then the value of A + B is
(1) – \(\frac{1}{2}\)
(2) – \(\frac{2}{3}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{2}{3}\)
Answer:
(1) – \(\frac{1}{2}\)
Explanation:
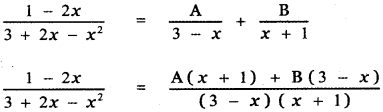
1 – 2x = A (x + 1) + B(3 – x) ——— (1)
Put x = – 1 in equation (1)
1 – 2 (- 1) = A (- 1 + 1) + B (3 + 1)
1 + 2 = 0 + 4B ⇒ B = \(\frac{3}{4}\)
Put x = 3 in equation (1)
1 – 2 × 3 = A(3 + 1) + B(3 – 3)
1 – 6 = 4A + 0
– 5 = 4A
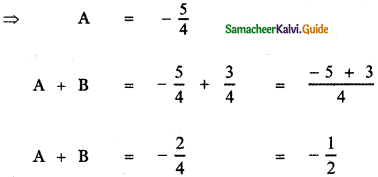
![]()
Question 19.
The number of roots of (x + 3)4 + (x + 5)4 = 16 is
(1) 4
(2) 2
(3) 3
(4) 0
Answer:
(1) 4
Explanation:
The equation is (x + 3)4 + (x + 5)4 = 16
(x + 3)4 + (x + 5)4 = 24
This is biquadratic equation. It has 4 roots.
Question 20.
The value of
log3 11 . log11 13 . log 13 15 . log 15 27 . log 27 81 is
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(4) 4
![]()
Explanation:
log3 11 . log11 13 . log 13 15 . log 15 27 . log 27 81
= log3 13 . log 13 15 . log 15 27 . log 27 81
= log 3 15 . log 15 27 . log 27 81
= log 3 27 . log 27 81
= log 3 81
= log 334
= 4 log 33
= 4 × 1
= 4