Category: Class 11

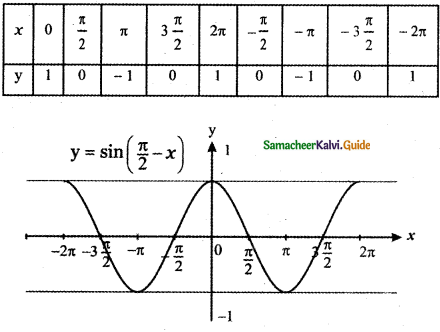
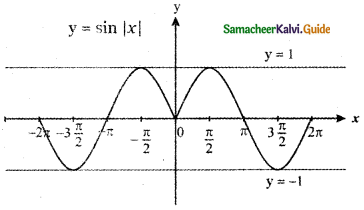
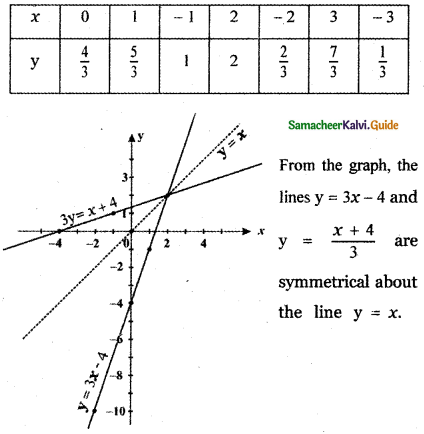
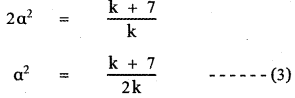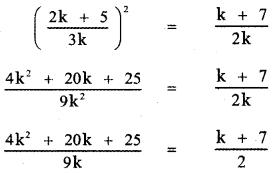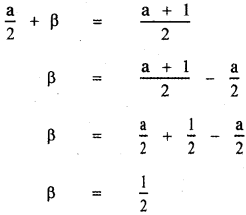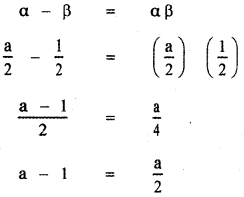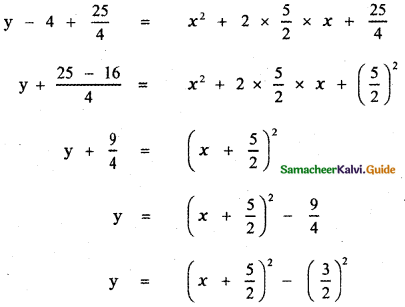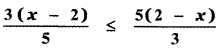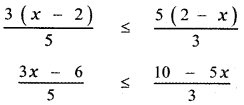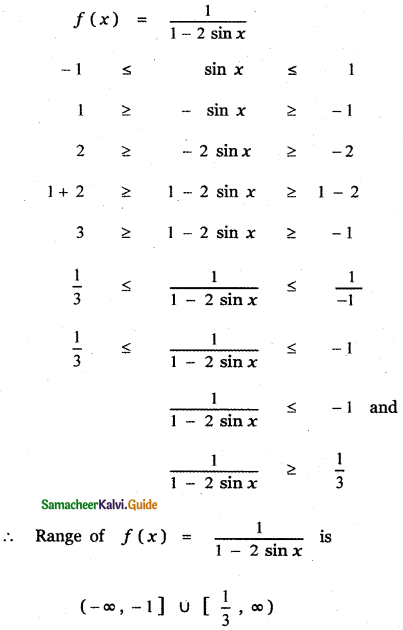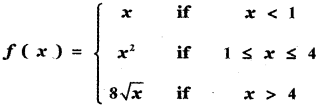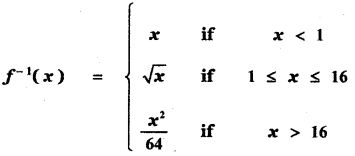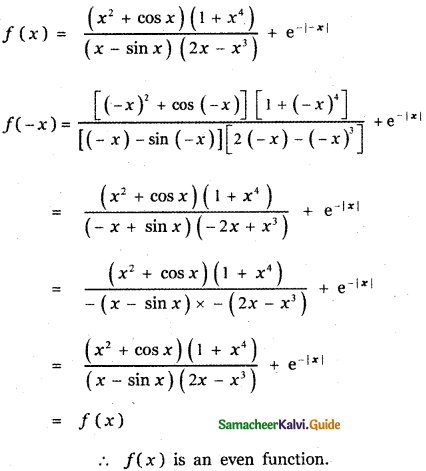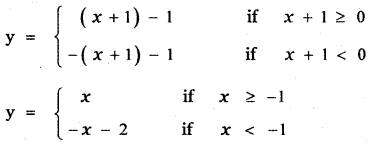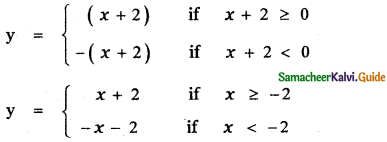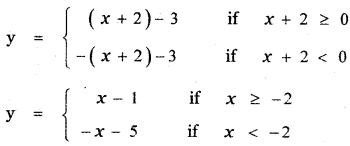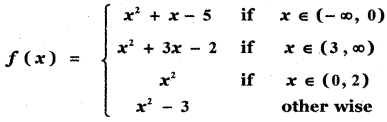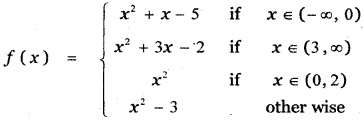Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.6 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.6

Question 1.
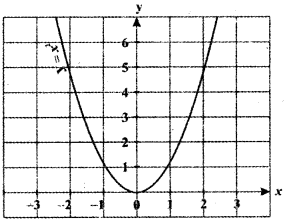
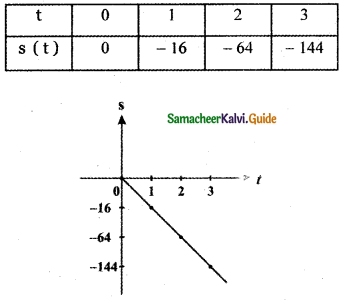
Find the zeros of the polynomial function f(x) = 4x² – 25
Answer:
Given f(x) = 4x² – 25
To find the zeors of f(x), put f(x) = 0
∴ 4x² – 25 = 0
⇒ 4x² = 25
⇒ x² = \(\frac{25}{4}\)
⇒ x = ±\(\sqrt{\frac{25}{4}}\) = ±\(\frac{5}{2}\)
Hence the zeros of f(x) are \(-\frac{5}{2}, \frac{5}{2}\)

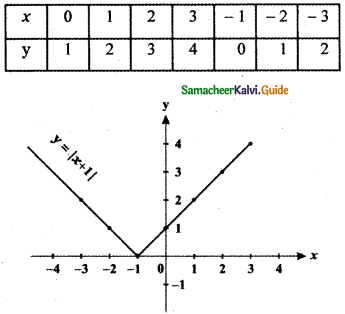
Question 2.
If x = – 2 is one root of x³ – x² – 17x = 22, then find the other roots of equation.
Answer:
Let f(x) = x³ – x² – 17x – 22 = 0 —– (1)
Given that x = – 2 is a root of f(x).
∴ x + 2 is a factor of f (x)
Using synthetic division

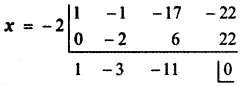
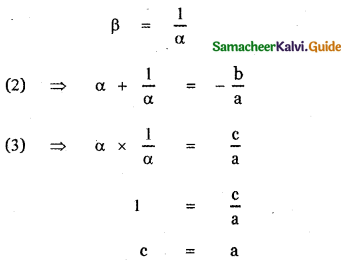
Comparing equation (1) with the equation ax² + bx + c = 0 we have
a = 1, b = – 3 , c = – 11

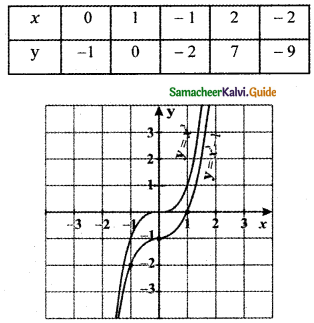
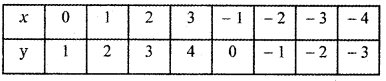
Question 3.
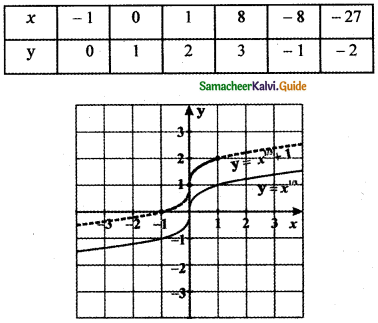
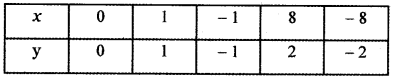
Find the real roots of x⁴ = 16.
Answer:
x⁴ = 16
⇒ x⁴ – 16 = 0
(i.e.,) x⁴ – 4² = 0
⇒ (x² + 4)(x² – 4) = 0
x² + 4 = 0 will have no real roots
so solving x² – 4 = 0
x² = 4

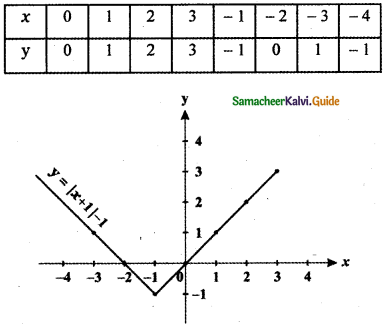
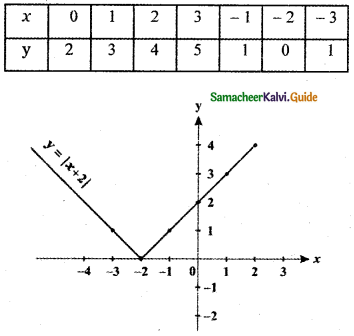
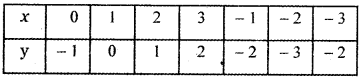
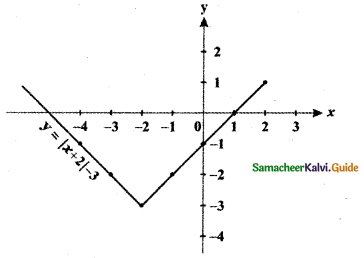
Question 4.
Solve (2x + 1)² – (3x + 2)² = 0
Answer:
The given equation is (2x + 1)² (3x + 2)² = 0
(2x + 1 + 3x + 2) [(2x + 1) – (3x + 2)] = 0
[a² – b² = (a + b) (a – b)]
(5x + 3) (2x + 1 – 3x – 2) = 0
(5x + 3)(- x – 1) = 0
– (5x + 3)(x + 1) = 0
5x + 3 = 0 or x + 1 = 0
x = – \(\frac{3}{5}\) or x = – 1
∴ Solution set is { – 1, \(\frac{3}{5}\)}

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.5

Question 1.
Solve 2x² + x – 15 ≤ 0
Answer:
The given inequality is
2x² + x – 15 ≤ 0 ——— (1)
2x² + x – 15 = 2x² + 6x – 5x – 15
= 2x (x + 3) – 5 (x + 3)
= (2x – 5)(x + 3)
2x² + x – 15 = 2\(\left(x-\frac{5}{2}\right)\))(x + 3) ——— (2)
The critical numbers are x – \(\frac{5}{2}\) = 0 or x + 3 = 0
The critical numbers are x = \(\frac{5}{2}\) or x = – 3
Divide the number line into three intervals

(i) (- ∞, – 3)
When x < – 3 say x = – 4
The factor x – \(\frac{5}{2}\) = – 4 – \(\frac{5}{2}\) < 0 and
x + 3 = – 4 + 3 = – 1 < 0
x – \(\frac{5}{2}\) < 0 and x + 3 < 0
⇒ \(\left(x-\frac{5}{2}\right)\) (x + 3) > 0
Using equation (2) 2x² + x – 15 > 0
∴ 2x² + x – 15 ≤ 0 is not true in (- ∞, – 3)

(ii) \(\left(-3, \frac{5}{2}\right)\)
When – 3 < x < \(\frac{5}{2}\) say x = 0
The factor x – \(\frac{5}{2}\) = 0 – \(\frac{5}{2}\) = – \(\frac{5}{2}\) < 0 and
x + 3 = 0 + 3 = 3 > 0
x – \(\frac{5}{2}\) < 0 and x + 3 > 0
⇒ \(\left(x-\frac{5}{2}\right)\) (x + 3) < 0
using equation (2) 2x² + x – 15 < 0
∴ 2x² + x – 15 ≤ 0 is true in \(\left(-3, \frac{5}{2}\right)\)

(iii) \(\left(\frac{5}{2}, \infty\right)\)
When x > \(\frac{5}{2}\) say x = 3
The factor x – \(\frac{5}{2}\) = 3 – \(\frac{5}{2}\) > 0 and
x + 3 = 3 + 3 > 0
x – \(\frac{5}{2}\) > 0 and x + 3 > 0
= \(\left(x-\frac{5}{2}\right)\) (x + 3) > 0
Using equation (2) 2x² + x – 15 > 0
∴ 2x² + x – 15 ≤ 0 is not true in \(\left(\frac{5}{2}, \infty\right)\)

We have proved the inequality 2x² + x – 15 ≤ 0 is true in the interval \(\left(-3, \frac{5}{2}\right)\)
But it is not true in the interval

Question 2.
Solve x² + 3x – 2 ≥ 0
Answer:
The given inequality is
– x² + 3x – 2 ≥ 0
x² – 3x + 2 < 0 ——– (1)
x² – 3x + 2 = x² – 2x – x + 2
= x(x – 2) – 1(x – 2)
x² – 3x + 2 = (x – 1) (x – 2) ——— (2)
The critical numbers are
x – 1 = 0 or x – 2 = 0
The critical numbers are
x = 1 or x = 2
Divide the number line into three intervals
(- ∞, 1), (1, 2) and (2, ∞).

(i) (- ∞, 1)
When x < 1 say x = 0
The factor x – 1 = 0 – 1 = – 1 < 0 and
x – 2 = 0 – 2 = – 2 < 0
x – 1 < 0 and x – 2 < 0
⇒ (x – 1)(x – 2) > 0
Using equation (2) x² – 3x + 2 > 0
∴ The inequality x² – 3x + 2 ≤ 0 is not true in the interval (- ∞, 1 )

(ii) (1, 2)
When x lies between 1 and 2 say x = \(\frac{3}{2}\)
The factor x – 1 = \(\frac{3}{2}\) – 1 = \(\frac{1}{2}\) > 0 and
x – 2 = \(\frac{3}{2}\) – 2 = – \(\frac{1}{2}\) – < 0
x – 1 > 0 and x – 2 < 0
⇒ (x – 1)(x – 2) < 0
Using equation (2) x² – 3x + 2 < 0
∴ The inequality x² – 3x + 2 ≤ 0 is true in the interval (1, 2 )

(iii) (2, ∞)
When x > 2 say x = 3
The factor x – 1 = 3 – 1 = 2 > 0 and
x – 2 = 3 – 2 = 1 > 0
x – 1 > 0 and x – 2 > 0
= (x – 1)(x – 2) > 0
Using equation (2) x² – 3x + 2 > 0
∴ The inequality x² – 3x + 2 ≤ 0 is not true in the interval (2, ∞)
We have proved the inequality x² – 3x + 2 ≤ 0 is true in the interval [ 1, 2 ].
But it is not true in the interval
(- ∞, 1) and (2, ∞)
∴ The solution set is [1, 2]

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.4

Question 1.
Construct a quadratic equation with roots 7 and – 3.
Answer:
The given roots are 7 and -3
Let α = 7 and β = -3
α + β = 7 – 3 = 4
αβ = (7)(-3) = -21
The quadratic equation with roots α and β is x² – (α + β) x + αβ = 0
So the required quadratic equation is
x² – (4) x + (-21) = 0
(i.e.,) x² – 4x – 21 = 0

Question 2.
A quadratic polynomial has one of its zero 1 + √5 and it satisfies p(1) = 2. Find the quadratic polynomial.
Answer:
Let p(x) = ax² + bx + c be the required quadratic polynomial.
Given p (1) = 2 , we have
a × 1² + b × 1 + c = 2
a + b + c = 2 ——— (1)
Also given 1 + √5 is a zero of p(x)
∴ a(1 + √5)² + b (1 + √5) + c = 0
a( 1 + 5 + 2√5) + b (1 + √5) + c = 0
6a + 2a√5 + b + b√5 + c = 0 ——— (2)
If 1 + √5 is zero then 1 – √5 is also a zero of p (x).
∴ a(1 – √5)² + b (1 – √5) + c = 0
a( 1 – 2√5 + 5) + b (1 – √5) + c = 0
6a – 2a√5 + b – b√5 + c = 0 ——— (3)

Substituting the value of a in equation (4)
5 × – \(\frac{2}{5}\) + 2 × – \(\frac{2}{5}\) × √5 + b√5 = – 2
– 2 – \(\frac{4}{5}\)√5 + b√5 = – 2
b√5 = – 2 + 2 + \(\frac{4}{5}\) . √5
b√5 = \(\frac{4}{5}\) . √5
b = \(\frac{4}{5}\)
Substituting the value of a and b in equation (1), we have

∴ The required quadratic polynomial is
p(x) = \(-\frac{2}{5}\)x² + \(\frac{4}{5}\)x + \(\frac{8}{5}\)
p(x) = \(-\frac{2}{5}\)(x² – 2x – 4)

Question 3.
If α and β are the roots of the quadratic equation x² + √2x + 3 = 0 form a quadratic polynomial with zeros \(\frac{1}{\alpha}, \frac{1}{\beta}\).
Answer:
Given α and β are the roots of the quadratic polynomial
x² + √2x + 3 = 0 ——— (1)

∴ The required quadratic equation whose roots are \(\frac{1}{\alpha}, \frac{1}{\beta}\) is
x² – (sum of the roots)x + product of the roots = 0

Question 4.
If one root of k (x – 1)² = 5x – 7 is double the other root, show that k = 2 or – 25
Answer:
The given quadratic equation is
k(x – 1)² = 5x – 7
k(x² – 2x + 1) – 5x + 7 = 0
kx² – 2kx + k – 5x + 7 = 0
kx² – (2k + 5)x + k + 7 = 0 ———- (1)
Let the roots be α and 2α
Sum of the roots α + 2α = –\(\frac{b}{a}\)

Product of te roots α(2α) = \(\frac{c}{a}\)

Using equation (2) and (3) we have

2(4k² + 20k + 25) = 9k(k + 7)
8k² + 40k + 50 = 9k² + 63k
9k² + 63k – 8k² – 40k – 50 = 0
k² + 23k – 50 = 0
k² + 25k – 2k – 50 = 0
k(k + 25) – 2(k + 25) = 0
(k – 2) (k + 25) = 0
k – 2 = 0 or k + 25 = 0
k = 2 or k = – 25

Question 5.
If the difference of the roots of the equation 2x² – (a + 1)x + a – 1 = 0 is equal to their product then prove that a = 2.
Answer:
The given quadratic equation is
2x² – (a + 1) x + a – 1 = 0 ———– (1)
Let α and β be the roots of the given equation
Given that α – β = αβ —— (2)
Sum of the roots α + β = – \(\frac{b}{a}\)


Substituting the values of α and β in equation (2)

2(a – 1) = a
2a – 2 – a = 0
a – 2 = 0
⇒ a = 2

Question 6.
Find the condition that one of the roots of ax² + bx + c may be
(a) negative of the other
(b) thrice the other
(c) reciprocal of the other.
Answer:
The given quadratic equation is
ax² + bx + c = 0 ——- (1)
Let α and β be the roots of the equation (1) then
Sum of the roots α + β = ——- (2)
Product of the roots αβ = ——- (3)

(a) Given one root is the negative of the other
β = – α
(2) ⇒ α + (-α) = – \(\frac{b}{a}\)
0 = – \(\frac{b}{a}\)
⇒ b = 0
(3) ⇒ α(-α) = \(\frac{c}{a}\)
– α² = \(\frac{c}{a}\)
Hence the required condition is b = 0

(b) Given that one root is thrice the other
β = 3α

When is the required condition?

(c) One root is reciprocal of the other

When is the required condition?

Question 7.
If the equations x² – ax + b = 0 and x² – ex + f = 0 have one root in common and if the second equation has equal roots then prove that ae = 2(b + f).
Answer:
The given quadratic equations are
x² – ax + b = 0 ———- (1)
x² – ex + f = 0 ——— (2)
Let α be the common root of the given quadratic equations (1) and (2)
Let α, β be the roots of x² – ax + b = 0
Sum of the roots α + β = \(-\left(-\frac{a}{1}\right)\)
α + β = a ———- (3)
Product of the roots αβ = \(\frac{b}{1}\)
αβ = b ——– (4)
Given that the second equation has equal roots.
∴ The roots of the second equation are a, a
Sum of the roots α + α = \(-\left(-\frac{e}{1}\right)\)
2α = e ——— (5)
Product of the roots α.α = \(\frac{f}{1}\)
α² = f ———- (6)
ae = (α + β)2α (Multiplying equations (3) and (5))
ae = 2α2 + 2αβ
ae= 2 (f) + 2b From equations (4) and (6)
ae= 2(f + b) Hence proved.

Question 8.
Discuss the nature of roots of
(i) – x² + 3x + 1 = 0
(ii) 4x² – x – 2 = 0
(iii) 9x² + 5x = 0.
Answer:
(i) -x² + 3x + 1 = 0
⇒ comparing with ax² + bx + c = 0
∆ = b² – 4ac = (3)² – 4(1)(-1) = 9 + 4 = 13 > 0
⇒ The roots are real and distinct

(ii) 4x² – x – 2 = 0
a = 4, b = -1, c = -2
∆ = b² – 4ac = (-1)² – 4(4)(-2) = 1 + 32 = 33 >0
⇒ The roots are real and distinct

(iii) 9x² + 5x = 0
a = 9, b = 5, c = 0
∆ = b² – 4ac = 5² – 4(9)(0) = 25 > 0
⇒ The roots are real and distinct

Question 9.
Without sketching the graphs, find whether the graphs of the following functions will intersect the x-axis and if so in how many points.
(i) y = x² + x + 2
(ii) y = x² – 3x – 7
(iii) y = x² + 6x + 9
Answer:
(i) y = x² + x + 2
y = x² + x + 2 ——— (1)
Compare this equation with the equation
ax² + bx + c = 0
we have a = 1 , b = 1, c = 2
b² – 4ac = 1² – 4 × 1 × 2 = 1 – 8
b² – 4ac = – 7 < 0
Since the discriminant is negative the quadratic equation has no real roots and therfore the graph does not meet x-axis.

(ii) y = x² – 3x – 7
y = x² – 3x – 7 ——— (2)
Compare this equation with the equation ax² + bx + c = 0
we have a = 1 , b = – 3 , c = – 1
b² – 4ac = (-3)² – 4(1)(-1)
= 9 + 4
b² – 4ac = 13 > 0
Since the discriminant is positive the quadratic equation has real and distinct roots and therefore the graph intersect the x – axis at two different points,

(iii) y = x² + 6x + 9
y = x² + 6x + 9 ——— (3)
Compare this equation with the equation
ax² + bx + c = 0
we have a = 1 , b = 6, c = 9
b² – 4ac = 6² – 4 × 1 × 9
= 36 – 36 =0
Since the discriminant is zero the quadratic equation has real and equal roots and therefore the graph touches the x-axis at one point.

Question 10.
Write f(x) = x² + 5x + 4 in completed square form.
Answer:
The given quadratic equation is
f(x) = x² + 5x + 4
Let y = x² + 5x + 4
y – 4 = x² + 5x

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.3

Question 1.
Represent the following inequalities in the interval notation:
(i) x ≥ – 1 and x < 4
Answer:
x ≥ – 1 and x < 4
x ∈ [- 1, 4)

(ii) x ≤ 5 and x ≥ – 3
Answer:
x ≤ 5 and x ≥ – 3
– 3 ≤ x ≤ 5
∴ x ∈ [- 3, 5 ]

(iii) x < – 1 or x < 3
Answer:
x < – 1 or x < 3
x ∈ (-∞, 3)

(iv) -2x > 0 or 3x – 4 < 11
Answer:
– 2x > 0 or 3x – 4 < 11
2x < 0 or 3x < 11 + 4
x < 0 or x < \(\frac{15}{3}\)
x < 0 or x < 5
x ∈ (- ∞, 5)

Question 2.
Solve 23x < 100 when
(i) x is a natural number,
(ii) x is an integer.
Answer:
Given 23x < 100
(i) When x is a natural number
23x < 100
⇒ x < \(\frac{100}{23}\)
⇒ x < 4.347
⇒ x = 1, 2, 3, 4
∴ The solution set is { 1, 2, 3 , 4 }

(ii) When x is an integer
23x < 100
⇒ x < \(\frac{100}{23}\)
⇒ x < 4.347
⇒ x = …… , – 3, – 2, – 1, 0, 1, 2, 3, 4
Hence the solution set is
{ ………, – 3, – 2, – 1, 0, 1 , 2 , 3 , 4 }

Question 3.
Solve – 2x ≥ 9 when
(i) x is a real number,
(ii) x is an integer
(iii) x is a natural number.
Answer:
Given – 2x ≥ 9
⇒ – x ≥ \(\frac{9}{2}\)
⇒ x ≤ \(-\frac{9}{2}\)

(i) When x is a real number
x ≤ \(-\frac{9}{2}\)
The solution set is \(\left(-\infty,-\frac{9}{2}\right]\)

(ii) x is an integer
x ≤ –\(-\frac{9}{2}\)
x ≤ – 4.5
x = …………., -7, – 6, -5

(iii) x is a natural number
x ≤ – \(\frac{9}{2}\)
x ≤ – 4.5
Since there exists no natural number less than – \(\frac{9}{2}\)
∴ No solution

Question 4.
Solve:
(i)
Answer:

3 (3x – 6) ≤ 5 (10 – 5x)
9x – 18 ≤ 50 – 25 x
9x + 25 x ≤ 50 + 18
34x ≤ 68
x ≤ \(\frac{68}{34}\) = 2
x ≤ 2
∴ The solution set is (-∞, 2]

(ii)
Answer:

Multiplying both sides by 3, we have
5 – x < \(\frac{3 x}{2}\) – 12
Multiplying both sides by 2, we have
10 – 2x < 3x – 24
10 + 24 < 3x + 2x
34 < 5x
\(\frac{34}{5}\) < x
x > \(\frac{34}{5}\)
∴ The solution set is \(\left(\frac{34}{5}, \infty\right)\)

Question 5.
To secure an A grade, one must obtain an average of 90 marks or more in 5 subjects each of a maximum of 100 marks. If one scored 84, 87, 95, 91 in the first four subjects, what is the minimum mark one scored in the fifth subject to get an A grade in the course?
Answer:
Required marks = 5 × 90 = 450
Total marks obtained in 4 subjects = 84 + 87 + 95 + 91 = 357
So required marks in the fifth subject = 450 – 357 = 93

Question 6.
A manufacturer has 600 litres of a 12 percent solution of acid. How many litres of a 30 percent acid solution must be added to it so that the acid content in the resulting mixture will be more than 15 percent but less than 18 percent?
Answer:
Amount of 12% solution of acid = 600 litres
Let x be the required number litres of 30 % acid solution to be added to the given 600 litres of 12 % acid solution to make the resulting mixture will be more than 15 % but less than 18 %.

∴ Total amount of mixture = (600 + x) litres
30% acid solution of x litres + 12% acid solution of 600 litres > 15% acid solution of (600 + x) litres
\(\frac{30}{100}\) × x + \(\frac{12}{100}\) × 600 > \(\frac{15}{100}\) × (600 + x)
30x + 7200 > 9000 + 15x
30x – 15x > 9000 – 7200
15x > 1800
x > \(\frac{1800}{15}\) = 120
x > 120 ——– (1)
Also 30% acid solution of x litres + 12% acid solution of 600 litres < 18% acid solution of ( 600 + x) litres.
\(\frac{30}{100}\) × x + \(\frac{12}{100}\) × 600 < \(\frac{15}{100}\) × (600 + x)
30x + 7200 < 18 (600 + x)
30x + 7200 < 10800 + 18x
30x – 18x < 10,800 – 7200
12x < 3600
x < \(\frac{3600}{12}\) = 300
x < 300 ——- (2)
From equations (1) and (2), we get ) 120 < x < 300
∴ The numbers of litres of the 30% acid solution to be added is greater than 120 litres and less than 300 litres.

Question 7.
Find all pairs of consecutive odd natural numbers both of which are larger than 10 and their sum is less than 40.
Answer:
Let x and x + 2 be the two pair of consecutive odd natural numbers.
Given x > 10 ——— (1)
and x + 2 > 10 ——— (2)
Also x + (x + 2) < 40 ——— (3)
From equations (1), we have
x = 11, 13 , 15, 17, 19, 21 …………
Using equation (3), the required pairs are
(11, 13), (13, 15), (15, 17), ( 17, 19), (19 ,21 ) is not possible since 19 + 21 = 40

Question 8.
A model rocket is launched from the ground. The height h reached by the rocket after t seconds from lift off is given by h(t) = – 5t² + 100t, 0 ≤ t ≤ 20. At what times, the rocket is 495 feet above the ground?
Answer:
h(t) = -5t² + 100t
at t = 0, h(0) = 0
at t = 1, h(1) = -5 + 100 = 95
at t = 2, h(2) = -20 + 200 = 180
at t =3, h(3) = -45 + 300 = 255
at t = 4, h(4) = -80 + 400 = 320
at t = 5, h(5) = -125 + 500 = 375
at t = 6, h(6) = – 180 + 600 = 420
at t = 7, h(7) = -245 + 700 = 455
at t = 8, h(8) = – 320 + 800 = 480
at t = 9, h(9) = -405 + 900 = 495
So, at 9 secs, the rocket is 495 feet above the ground.

Question 9.
A plumber can be paid according to the following schemes: In the first scheme he will be paid rupees 500 plus rupees 70 per hour and in the second scheme, he will pay rupees 120 per hour. If he works x hours, then for what value of x does the first scheme give better wages?
Answer:
I scheme with x hr
500 + (x- 1) 70 = 500 + 70x – 70 = 430 + 70x
II scheme with x hours
120x
Here I > II
⇒ 430 + 70x > 120x
⇒ 120x – 70x < 430
50x < 430
\(\frac{50 x}{50}<\frac{430}{50}\)
x < 8.6 (i.e.) when x is less than 9 hrs the first scheme gives better wages.

Question 10.
A and B are working on similar jobs but their monthly salaries differ by more than Rs. 6000. If B earns rupees 27,000 per month, then what are the possibilities of A’s salary per month?
Answer:
A’s monthly salary = ₹ x
B’s monthly salary = ₹ 27000
Their annual salaries differ by ₹ 6000
A’s salary – 27000 > 6000
A’s salary > ₹ 33000
B’s salary – A’s salary > 6000
27000 – A’s salary > 6000
A’s salary < ₹ 21000
A’s monthly salary will be lesser than ₹ 21,000 or greater than ₹ 33,000

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.2

Question 1.
Solve for x
(i) |3 – x| < 7
Answer:
-7 < 3 – x < 7 3 – x > -7
-x > -7 -3 (= -10)
-x > -10 ⇒ x < 10
3 – x < 7
– x < 7 – 3 (= 4)
– x < 4x > -4 … .(2)
From (1) and (2)
⇒ x > -4 and x < 10
⇒ -4 < x < 10

(ii) |4x – 5| ≥ – 2
Answer:
|4x – 5| ≥ -2
(4x – 5) ≤ -(-2) or (4x – 5) ≥ -2
(4x – 5) ≤ 2 or (4x – 5) ≥ -2
4x ≤ 2 + 5 or 4x ≥ -2 + 5

∴ x ∈ (-∞, ∞) = R

(iii) |3 – \(\frac{3}{4}\)x| ≤ \(\frac{1}{4}\)
Answer:

Multiplying by 4, we have
– 13 ≤ – 3x ≤ – 11 ——– (1)
We know that a < b ⇒ \(\frac{\mathrm{a}}{\mathrm{y}}\) > \(\frac{\mathrm{b}}{\mathrm{y}}\) when y < 0
Divide equation (1) by – 3, we have

(iv) |x| – 10 < – 3
Answer:
|x| – 10 < – 3
|x| < – 3 + 10
|x| < 7
– 7 < x < 7
∴ The solution set is (-7, 7)

Question 2.
Solve \(\frac{1}{|2 x-1|}\) < 6 and express the solution using the interval notation.
Answer:

Question 3.
Solve – 3 |x| + 5 ≤ – 2 and graph the solution set in a number line.
Answer:
-3|x| + 5 ≤ – 2
⇒ -3 |x| ≤ – 2 – 5 (= -7)
-3|x| ≤ – 7 ⇒ 3 |x| ≥ 7

Question 4.
SoIve 2|x + 1| – 6 ≤ 7 and graph the solution set in a number line.
Answer:
Given 2|x + 1| – 6 ≤ 7
2|x + 1| ≤ 7 + 6
2|x + 1| ≤ 13
|x + 1| ≤ \(\frac{13}{2}\)

Question 5.
Solve \(\frac{1}{5}\) |10x – 2| < 1
Answer:
Given \(\frac{1}{5}\) |10x – 2| < 1
|10x – 2| < 5
-5 < (10x – 2) < 5
– 5 + 2 < 10x < 5 + 2
– 3 < 10x < 7
\(-\frac{3}{10}\) < x < \(\frac{7}{10}\)
∴ The solution set is x ∈ \(\left(-\frac{3}{10}, \frac{7}{10}\right)\)

Question 6.
Solve |5x – 12| < – 2
Answer:
By the definition of modulus function. |5x – 12| always positive.
∴ |5x – 12| < -2 is not possible.
∴ Solution does not exist.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.1

Question 1.
Classify each element of {√7, \(-\frac{1}{4}\), 0, 3.14 , 4, \(\frac{22}{7}\)} as a member of N, Q, R – Q or Z.
Answer:
√7 is an irrational number. ∴ √7 ∈ R – Q
\(-\frac{1}{4}\) is a negative rational number. ∴ \(-\frac{1}{4}\) ∈ Q
0 is an integer. ∴ 0 ∈ Z , Q
3.14 is a rational number. ∴ 3.14 ∈ Q
4 is a positive integers. ∴ 4 ∈ Z, N, Q
\(\frac{22}{7}\) is an rational number. ∴ \(\frac{22}{7}\) ∈ Q

Question 2.
Prove that √3 is an irrational number.
Answer:
Suppose that √3 is rational. Let √3 = \(\frac{\mathrm{m}}{\mathrm{n}}\) where m and n are positive integers with no common factors greater than 1.
√3 = \(\frac{\mathrm{m}}{\mathrm{n}}\)
⇒ √3n = m
⇒ 3n² = m² ——– (1)
By assumption n is an integer
∴ n² is an integer. Hence 3n² is an integral multiple of 3.
∴ From equation (1) m² is an integral multiple of 3
⇒ m is an intergral multiple of 3

[Here m is an integer and m² is an integral multiple of 3. That m² is cannot take all integral multiples of 3. For example suppose m² = 3 = 1 × 3 which is an integral multiple of 3. In this case m = √3 which is not an integer. Suppose m² = 6 = 2 × 3 which is an integer multiple of 3 , but m = √2 √3 which is an integer. Hence m² is an integral multiple of 3. Such that m is an integer.
Examples: m² = 4 × 9,
m² = 9,
m² = 9 × 9 etc.]

Let m = 3k
where k is an integer
Using equation (1) we have
3n² = (3k)²
⇒ 3n² = 9k²
⇒ n² = 3k²
∴ n² is an integral multiple of 3. Since, n is an integer, we have n is also an integral multiple of 3.

Thus we have proved both m and n are integral multiple of 3. Hence both m and n have common factor 3, which is a contradiction to our assumption that m and n are integers with no common factors greater than 1.

Hence our assumption that √3 is a rational number is wrong.
∴ √3 is an irrational number.

Question 3.
Are there two distinct irrational numbers such that their difference is a rational number? Justify.
Answer:
Taking two irrational numbers as 3 + \(\sqrt{2}\) and 1 + \(\sqrt{2}\)
Their difference is a rational number. But if we take two irrational numbers as 2 – \(\sqrt{3}\) and 4 + \(\sqrt{7}\).
Their difference is again an irrational number. So unless we know the two irrational numbers we cannot say that their difference is a rational number or irrational number.

Question 4.
Find two irrational numbers such that their sum is a rational number. Can you find two irrational numbers whose product is a rational number?
Answer:
(i) Let the two irrational numbers as 2 + \(\sqrt{3}\) and 3 – \(\sqrt{3}\)
Their sum is 2 + \(\sqrt{3}\) + 3 – 3\(\sqrt{3}\) which is a rational number.
But the sum of 3 + \(\sqrt{5}\) and 4 – \(\sqrt{7}\) is not a rational number. So the sum of two irrational numbers is either rational or irrational.

(ii) Again taking two irrational numbers as π and \(\frac{3}{\pi}\) their product is \(\sqrt{3}\) and \(\sqrt{2}\) = \(\sqrt{3}\) × \(\sqrt{2}\) which is irrational, So the product of two irrational numbers is either rational or irrational.

Question 5.
Find a positive number smaller than \(\frac{1}{2^{1000}}\) Justify.
Answer:
The given number is \(\frac{1}{2^{1000}}\)
We have 1000 < 1001
⇒ 2¹⁰⁰⁰ < 2¹⁰⁰¹
⇒ \(\frac{1}{2^{1000}}\) > \(\frac{1}{2^{1001}}\)
∴ A positive number smaller than \(\frac{1}{2^{1000}}\) is \(\frac{1}{2^{1001}}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 Sets, Relations and Functions Ex 1.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets, Relations and Functions Ex 1.5

Choose the correct or the most suitable answer.

Question 1.
If A = {(x,y): y = e^x, x ∈ R} and B = {(x, y): y = e^-x, x ∈ R},then n(A ∩ B) is
(1) Infinity
(2) 0
(3) 1
(4) 2
Answer:
(3) 1

Explaination:
Given
A = {(x,y): y = e^x, x ∈ R}
B = {(x,y): y = e^-x, x ∈ R}
Consider the curve y = e^x
When x = 0 ⇒ y = e^-0 = 1
When x = ∞ ⇒ y = e^-∞ = ∞
When x = -∞ ⇒ y = e^∞ = 0

Consider the curve y = e^-x.
When x = 0 ⇒ y = e^-0 = 1
When x = ∞ ⇒ y = e^-∞ = 0
When x = -∞ ⇒ y = e^∞ = ∞


(0, 1) is the only point common to y = e<sup.x and y = e^-x
∴ A ∩ B = {(0,1)} ⇒ n (A ∩ B ) = 1

Question 2.
If A = { ( x, y): y = sin x, x ∈ R } and B = { ( x, y): y = cos x, x ∈ R} then A ∩ B contains
(1) no element
(2) infinitely many elements
(3) only one element
(4) cannot be determined
Answer:
(2) infinitely many elements

Explaination:
Given A = { (x, y): y = sin x, x ∈ R}
B = {(x, y): y = cos x, x ∈ R }
Consider the equations y = sin x and y = cos x
sin x = cos x ⇒ \(\frac{\sin x}{\cos x}\) = 1
tan x = 1 ⇒ x = nπ + \(\) for n ∈ z
There are infinite number of common points for the sets A and B

Question 3.
The relation R defined on a set A = {0, -1, 1, 2} by x R y if |x² + y²| ≤ 2,
then which one of the following is true.
(1) R = {(0,0), (0,-1), (0,1), (-1,0), (-1,1), (1,2), (1,0)}
(2) R^-1 = {(0, 0), (0, -1), (0, 1), (-1, 0), (1, 0)}
(3) Domain of R is {0,- 1, 1, 2}
(4) Range of R is {0, -1, 1}
Answer:
(4) Range of R is {0, -1, 1}

Explaination:
A= {0, -1, 1, 2}
|x² + y²| ≤ 2
The values of x and y can be 0, -1 or 1
So range = {0, -1, 1}

Question 4.
If f(x) = |x – 2 | + |x + 2| x ∈ R then
(1)
(2)
(3)
(4)

Answer:
(1)

Explaination:
f(x) = |x – 2| + |x + 2|, x ∈ R
Divide the Real line into three intervals

In the interval (2, ∞), both the factors x – 2 and x + 2 are positive.
∴ f(x) = x – 2 + x + 2 = 2x
f(x) = 2x for all x ∈ (2, ∞)

In the interval (- ∞, – 2 ] both the factors x – 2 and x + 2 are negative.
∴ f(x) = – (x – 2) – (x + 2)
= – x + 2 – x – 2 = – 2x
∴ f(x) = – 2x for all x ∈ (- ∞,- 2]

In the interval (—2, 2], the factor x – 2 is negative and the factor x + 2 is positive.
∴ f(x) = – (x – 2) + (x + 2)
f(x) = – x + 2 + x + 2 = 4
Thus f(x) = 4 for all x ∈ (- 2, – 2]

Question 5.
Let R be the set of all real numbers. Consider the following subsets of the plane R × R:
S = { (x, y): y = x + 1 and 0 < x < 27 and
T = {(x, y): x – y is an integer} Then which of the following is true?
(1) T is an equivalence relation but S Is not an equivalence relation
(2) Neither S nor T is an equivalence relation
(3) Both S and T are equivalence relation
(4) S is an equivalence relation but T is not an equivalence relation.
Answer:
(1) T is an equivalence relation but S Is not an equivalence relation

Explanation:
(0, 1), (1, 2) it is not an equivalence relation
T is an equivalence relation

Question 6.
Let A and B be subsets of the universal set N, the set of natural numbers. Then A’ ∪ [(A ∩ B) ∪ B’] is
(1) A
(2) A’
(3) B
(4) N
Answer:
(4) N

Explaination:
Let N = {1, 2, 3, ……….. 10}
A = { 1, 2, 3, 4, 5 }
B = {6, 7, 8, 9, 10}
A’ = {6, 7, 8, 9, 10 }
B’ = { 1 , 2, 3, 4, 5 }
A ∪ B = {1, 2, 3, 4, 5} ∪ {6, 7, 8, 9, 10}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(A ∪ B) ∩ B’ = {1,2, 3, 4, 5, 6,7, 8, 9,10} ∩ { 1, 2, 3, 4 , 5 }
(A ∪ B) ∩ B’= {1,2, 3,4, 5}
A’ ∪ [(A ∪ B ) ∩ B’] = { 6, 7, 8, 9 , 10 } ∪ {1, 2, 3, 4, 5 }
= {1, 2, 3, 4,5, 6, 7, 8, 9, 10}
A’ ∪ [(A ∪ B) ∩ B’] = N

Question 7.
The number of students who take both the subjects Mathematics and Chemistry is 70. This represents 10% of the enrollment in Mathematics and 14% of the enrollment in Chemistry. The number of students takes atleast one of these two subjects, is
(1) 1120
(2) 1130
(3) 1100
(4) Insufficient data
Answer:
(2) 1130

Explanation:
n(M ∪ C) = n(M) + n(C) – n(M ∩ C)
= 700 + 500 – 70
= 1130

Question 8.
If n[ (A × B) n (A × C) ] = 8 and n(B ∩ C) = 2 then n(A) is
(1) 6
(2) 4
(3) 8
(4) 16
Answer:
(2) 4

Explaination:
Given n[(A × B) n (A × C)] = 8
n(B ∩ C) = 2
n[(A × B) ∩ (A × C)] = 8
A × (B ∩ C) = (A × B) ∩ (A × C) ]
⇒ n [A × (B ∩ C)] = 8
⇒ n(A) . n (B ∩ C) = 8
⇒ n(A). 2 = 8
⇒ n(A) = \(\frac{8}{2}\) = 4

Question 9.
If n(A) = 2 and n(B ∪ C) = 3,then n[(A × B) ∪ (A × C)] is
(1) 2³
(2) 3²
(3) 6
(4) 5
Answer:
(3) 6

Explaination:
n[(A × B) ∪ (A × C)] = n[ A × (B ∪ C)] = n(A) × n(B ∪ C)
= 2 × 3
= 6

Question 10.
If two sets A and B have 17 elements in common, then the number of elements common to the set A × B and B × A is
(1) 2¹⁷
(2) 17²
(3) 34
(4) Insufficient data
Answer:
(2) 17²

Explanation:
If two sets A and B have 17 elements in common, then the number of elements common to the set A × B
and B × A is 17²

Question 11.
For non-empty sets A and B, if A ⊂ B then (A × B) ∩ (B × A) is equal to
(1) A ∩ B
(2) A × A
(3) B × B
(4) None of these
Answer:
(2) A × A

Explanation:
When A ⊂ B, (A × B) ∩ (B × A) = A × A

Question 12.
The number of relations on a set containing 3 elements is
(1) 9
(2) 81
(3) 512
(4) 1024
Answer:
(3) 512

Explanation:
The number of relations on a set containing n elements is 2ⁿ². Here n = 3
∴ Required number = 2³² = 2⁹
= 512

Question 13.
Let R be the universal relation on a set X with more than one element. Then R is
(1) not reflexive
(2) not symmetric
(3) transitive
(4) none of the above
Answer:
(3) transitive

Explanation:
Given R is a universal relation on the set X.
The universal relation is always an equivalence relation.
R is reflexive, symmetric, and transitive.

Question 14.
Let X = { 1, 2, 3, 4 } and R = { ( 1, 1 ), (1, 2), (1, 3), (2, 2), (3, 3), (2, 1), (3, 1), (1, 4), ( 4, 1) } . Then R is
(1) Reflexive
(2) Symmetric
(3) Transitive
(4) Equivalence
Answer:
(2) Symmetric

Explanation:
(4, 4} ∉ R ⇒ R is not reflexive
(1, 4), (4, 1) ∈ R ⇒ R is symmetric
(1, 4), (4, 1) ∈ R but (4, 4) ∉ R
So R is not transitive

Question 15.
The range of the function \(\frac{1}{1-2 \sin x}\) is
(1) (- ∞, – 1) ∪ (\(\frac{1}{3}\), ∞)
(2) (-1, \(\frac{1}{3}\))
(3) [-1, \(\frac{1}{3}\)]
(4) (- ∞, – 1] ∪ [\(\frac{1}{3}\), ∞)
Answer:
(4) (- ∞, – 1] ∪ [\(\frac{1}{3}\), ∞)

Explaination:

Question 16.
The range of the function
f(x) = |[x] – x|, x ∈ R is
(1) [0, 1]
(2) [0, ∞)
(3) [0, 1)
(4) (0, 1)
Answer:
(3) [0, 1)

Explaination:
f(x) = |[x] – x|
When x = 1 ,
we have [x] = [1] = 1
f(1) = |1 – 1| = o

When x = 1.5
we have [x} = [1.5] = 1
f(1.5) = |1 – 1.5| = |- 0.5| = 0.5

When x = 2.5
we have [x] = [2.5] = 2
f (2.5) = |2 – 2.5| = |- 0.5| = 0.5

When x = – 2.5
we have [x] = [- 2.5] = – 3
f (-2.5) = |- 3 – (-2.5| = |- 3 + 0.5| = |- 0.5| = 0.5
∴ Range of f(x) = |[x] – x| is [0, 1)

Question 17.
The rule f(x) = x² is a bijection if the domain and the co – domain are given by
(1) R, R
(2) R,(0, ∞)
(3) (0, ∞)R
(4) [0, ∞), [0, ∞)
Answer:
(4) [0, ∞), [0, ∞)

Explaination:
Let x ∈ R, then x can be negative or zero or positive.
Given f(x) = x²
The image of x under f is always positive since x² is positive for x = 1 and x = – 1 ∈ R
f(1) = 1² = 1
f(-1) = (-1)² = 1
∴ 1, – 1 have the same image
∴ f is not one – one if the domain is R.
Suppose the domain is [0, ∞) then f is one – one and onto.
Domain = [0, ∞)
Co-domain = [0, ∞)

Question 18.
The number of constant functions from a set containing m elements to a set containing n elements is
(1) mn
(2) m
(3) n
(4) m + n
Answer:
(3) n

Explanation:
Let A be a set having m elements and B be a set having n elements.
When all the elements of A mapped onto the first element of B we get the first constant function. When all the elements of A mapped onto the second element of B we get the second constant function.

When all the elements of A mapped on to the n^th element of B, we get the n^th constant function.
∴ The number of constant functions possible is n.

Question 19.
The function f:[0, 2π] → [- 1, 1] defined by f(x) = sin x is
(1) one to one
(2) onto
(3) bijection
(4) cannot be defined
Answer:
(2) onto

Explaination:
f : [0, 2π] → [- 1, 1]
Defined by f (x) = sin x
f(0) = sin 0 = 0

Question 20.
If the function f : [-3, 3] → S defined by f(x ) = x² is onto, then S is
(1) [-9, 9]
(2) R
(3) [-3, 3]
(4) [0, 9]
Answer:
(4) [0, 9]

Explaination:
f: [-3, 3] → S defined by f(x) = x²
f(-3) = (-3)² = 9
f(0) = 0² = o
f(3) = 3² = 9
∴ S = [0, 9]

Question 21.
Let X = {1, 2, 3, 4}, Y = { a, b , c, d } and f = {(1, a), (4, b), (2, c), (3, d), (2, d)}. Then f is
(1) an one – to – one function
(2) an onto function
(3) a function which is not one to one
(4) not a function
Answer:
(4) not a function

Explaination:
X = {1, 2, 3, 4}, Y = {a, b, c, d>
f = {(1, a), (4, b), (2, c), (3, d), (2, d)}

f is not a function since 2 ∈ X has two images c and d.

Question 22.
The inverse of

(1)
(2)
(3)
(4)
Answer:
(1)

Explaination:

Let f(x) = x if x < 1 —— (1)
Put y = x then
(1) ⇒ f(x) = y
⇒ x = f^-1(y) if y < 1
⇒ y = f^-1(y) if y < 1
⇒ f^-1(x) = x if x < 1
Let f(x) = x² if 1 ≤ x ≤ 4 —– (2)
Put y = x² ⇒ x = √y, if 1 ≤ y ≤ 16
then (2) ⇒ f(x) = y
⇒ x = f^-1(y) if 1 ≤ y ≤ 16
⇒ √(y) = f^-1(y) if 1 ≤ y ≤ 16
⇒ √x = f^-1(y) if 1 ≤ x ≤ 16
Let f(x) = 8√x if x > 4 ———– (3)
Put y = 8√x ⇒ y² = 64 x
⇒ x = \(\frac{y^{2}}{64}\) if y>16
then (3) ⇒ f(x) = y
⇒ x = f^-1(y) if y > 16
⇒ √y = f^-1(y) if y > 16
⇒ \(\frac{y^{2}}{64}\) = f^-1(x) if x > 16

Question 23.
Let f: R → R be defined by f(x) = 1 – |x|. Then the range of f is
(1) R
(2) (1, ∞)
(3) (-1, ∞)
(4) (- ∞, 1)
Answer:
(4) (- ∞, 1)

Explaination:
f: R ➝ R defined by
f(x) = 1 – |x|
For example,
f(1) = 1 – 1 = 0
f(8) = 1 – 8 = -1
f(-9) = 1 – 9 = -8
f(-0.2) = 1 – 0.2 = 0.8
so range = (-∞, 1]

Question 24.
The function f : R → R be defined by f(x) = sin x + cos x is
(1) an odd function
(2) neither an odd function nor an even function
(3) an even function
(4) both odd function and even function
Answer:
(2) neither an odd function nor an even function

Explaination:
f : R → R is defined by f(x) = sin x + cos x
f(-x) = sin (-x) + cos (-x) = -sin x + cos x ≠ f (x)
If f(-x) = -f(x) then f(x) is an odd function.
If f(-x) = f(x) then f(x) is an even function.
∴ f (x) is neither odd function nor an even function.

Question 25.
The function f : R → R be defined by

(1) an odd function
(2) neither an odd function nor an even function
(3) an even function
(4) both odd function and even function.
Answer:
(3) an even function

Explanation:

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 Sets, Relations and Functions Ex 1.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets, Relations and Functions Ex 1.4

Question 1.
For the curve y = x³ given in figure below, draw
(i) y = – x³
(ii) y = x³ + 1
(iii) y = x³ – 1
(iv) y = (x + 1)³ with the same scale.

Answer:
(i) y = – x³

The graph y = – x³ is the reflection of the graph y = x³ about x-axis.
The graph of y = – f( x) is the reflection of the graph of y = f( x) about x – axis.

(ii) y = x³ + 1

The graph of y = x³ + 1, causes the graph y = x³ a shift to the upward by 1 unit.
The graph of y = f(x) + d, d > 0 causes the graph y = f(x) a shift to the upward by d units.

(iii) y = x³ – 1

The graph of y = x³ – 1, causes the graph y = x³ a shift to the downward by 1 unit.
The graph of y = f(x) – d, d > 0 causes the graph y = f(x) a shift to the downward by d units.

(iv) y = (x + 1)⁰⁰³³

The graph y = (x + 1)³ causes the graph of y = x³ a shift to the left by 1 unit.
The graph of y = f(x + c), c > 0 causes the graph y = f(x) a shift to the left by c units.

Question 2.
For the given curve y = x^1/3 given in figure draw
(i) y = – x^1/3
(ii) y = x^1/3 + 1
(iii) y = x^1/3 – 1
(iv) y = (x + 1)^1/3
Answer:

(i) y = – x^1/3
-y = x^1/3
(-y)³ = x
-y³ = x
When y = 0 ⇒ – 0³ ⇒ x = 0
y = 1 ⇒ – 1³ = x ⇒ x = – 1
y = 2 ⇒ – 2³ = x ⇒ x = – 8
y = 3 ⇒ – 3³ = x ⇒ x = – 27
y = -1 ⇒ – (-1)³ = x ⇒ x = 1
y = -2 ⇒ – (-2)³ = x ⇒ x = 8
y = -3 ⇒ – (- 3)³ = x ⇒ x = 27

The graph of y = – x^1/3 is the reflection of the graph of y = x^1/3 about the x-axis.
The graph of y = – f(x) is the reflection of the graph of y = f(x) about x – axis.

(ii) y = x^1/3 + 1
y – 1 = x^1/3
⇒ (y – 1)³ = x

When
y = 0 ⇒ (0 – 1 )³ = x ⇒ x = – 1
y = 1 ⇒ (1 – 1)³ = x ⇒ x = 0
y = 2 ⇒ ( 2 – 1 )³ = x ⇒ x = 1
y = 3 ⇒ (3 – 1)³ = x ⇒ x = 8
y = -1 ⇒ (-1 – 1)³ = x ⇒ x = – 8
y = -2 ⇒ (-2 – 1)³ = x ⇒ x = – 27

The graph of y = x^1/3 + 1 causes the graph y = x^1/3 a shift to the upward by 1 unit.
The graph of y = f(x) + d, d > 0 causes the graph y = f(x) a shift to the upward by d units.

(iii) y = x^1/3 – 1
y + 1 = x^1/3
( y + 1)³ = x
When
y = 0 ⇒ (0 + 1)³ = x ⇒ x = 1
y = 1 ⇒ ( 1 + 1)³ = x ⇒ x = 8
y = 2 ⇒ (2 + 1)³ = x ⇒ x = 27
y = – 1 ⇒ (-1 + 1)³ = x ⇒ x = 0
y = – 2 ⇒ (-2 + 1)³ = x ⇒ x = – 1
y = – 3 ⇒ (-3 + 1)³ = x ⇒ x = – 8

The graph of y = x^1/3 – 1 causes the graph y = x^1/3 a shift to the downward by 1 unit.
The graph of y = f(x) – d, d > 0 causes the graph y = f(x) a shift to the downward by d units.

(iv) (x + 1)^1/3
y³ = x + 1
When
y = 0 ⇒ 0³ = x + 1 ⇒ x = -1
y = 1 ⇒ 1³ = x + 1 ⇒ x = 0
y = 2 ⇒ 2³ = x + 1 ⇒ x = 8 – 1 = 7
y = 3 ⇒ 3³= x + 1 ⇒ x = 27 – 1 = 26
y = – 1 ⇒ (-1)³ = x + 1 ⇒ x = – 1 – 1 = – 2
y = -2 ⇒ (-2)³ = x + 1 ⇒ x = – 8 – 1 = – 9

The graph of y = (x + 1)³ causes the graph y = x^1/3 a shift to the left by 1 unit.
The graph of y = f(x + c), c > 0 causes the graph y = f(x) a shift to the left by c units.

Question 3.
Graph the functions f(x) = x³ and g (x) = \(\sqrt[3]{x}\) on the same coordinate plane. Find fog and the graph it on the plane as well. Explain your results.
Answer:
Given functions are f(x) = x3 and g(x) = x^1/3
fog (x) = f(g(x))
= f\(\left(x^{\frac{1}{3}}\right)\)
= \(\left(x^{\frac{1}{3}}\right)^{3}\) = x
f(x) = x³

g(x) = x^1/3

Graph of fog(x) = x

Since fog(x) = x is symmetric about the line y = x, g(x) is the inverse image of f(x).
∴ g(x) = f^-1(x)

Question 4.
Write steps to obtain the graph of the function y = 3 (x – 1 )² + 5 from the graph y = x²
Answer:
Step 1:
Draw the graph y = x²

Step 2:
The graph of y = (x – 1)² shifts to the right for one unit.

The graph of y = (x – 1 )² shifts the graph
y = x² to the right by 1 unit.
The graph of y = f(x – c), c > 0 causes the graph y = f(x) a shift to the right by c units.

Step 3:
The graph of y = 3 (x – 1)² compresses towards y – axis that is moves away from the x – axis since the multiplying factor is which is greater than 1.

The graph of y = 3 (x – 1)² compresses the graph y = (x – 1)² towards the y-axis that is moving away from the x-axis since the multiplying factor is greater than 1.

For the graph y = kf(x), If k is a positive constant greater than one, the graph moves away from the x-axis. If k is a positive constant less than one, the graph moves towards the x-axis.

Step 4:
The graph of y = 3(x – 1)² + 5 causes the shift to the upward for 5 units.


The graph of y = 3(x – 1)² + 5 causes the graph y = 3(x – 1)² shifts to the upward for 5 units.

The graph of y = f(x) + d, d > 0 causes the graph y = f(x) a shift to the upward by d units.

Question 5.
From the curve y = sin x, graph the functions.
(i) y = sin (- x)
(ii) y = -sin(-x)
(iii) y = sin\(\left(\frac{\pi}{2}+x\right)\) which is cos x
(iv) y = sin\(\left(\frac{\pi}{2}-x\right)\) which is also cos x
(Refer Trigonometry )
Answer:
y = sin x

(i) y = sin(-x)
y = – sin x

The graph of y = sin (- x) is the reflection of the graph of y = sin x about y-axis.
The graph of y = f(- x) is the reflection of the graph of y = f(x) about y – axis.

(ii) y = – sin (-x)
y = sin x


y = – sin (-x) is the reflection of y = sin (-x) about the x – axis.
The graph of y = – f( x) is the reflection of the graph of y = f( x) about x – axis.

(iii) y = sin\(\left(\frac{\pi}{2}+x\right)\)


The graph of y = sin \(\left(\frac{\pi}{2}+x\right)\) causes y = sin x a shift to the left by \(\frac{\pi}{2}\) units.
The graph of y = f(x + c), c > 0 causes the graph y = f(x) a shift to the left by c units.

(iv) y = sin\(\left(\frac{\pi}{2}-x\right)\)



The graph of sin \(\left(\frac{\pi}{2}-x\right)\) causes the graph y = sin x a shift to the right by \(\frac{\pi}{2}\) unit.

The graph of y = f(x – c), c > 0 causes the graph y = f(x) a shift to the right by c units.

Question 6.
From the curve y = x draw
(i) y = -x
(ii) y = 2x
(iii) y = x + 1
(iv) y = \(\frac{1}{2}\)x + 1
(v) 2x + y + 3 = 0
Answer:

(i) y = -x

Graph of y = – x is the reflection of the graph of y = x about the x – axis.
The graph of y = – f(x) is the reflection of the graph of y = f(x) about x – axis.

(ii) y = 2x

The graph of y = 2x compresses the graph y = x towards the y-axis that is moving away from the x-axis since the multiplying factor is 2 which is greater than 1.

The graph of y = k f(x), k > 0 moves away from the x-axis if k is greater than 1.

(iii) y = x + 1


The graph of y = x + 1 causes the graph y = x shift to upward by 1 unit.

The graph of y = f(x) + d, d > 0 causes the graph y = f(x) a shift to the upward by d units.

(iv) y = \(\frac{1}{2}\)x + 1
When
x = 0 ⇒ y = \(\frac{1}{2}\) × 0 + 1 = 1
x = 2 ⇒ y = \(\frac{1}{2}\) × 2 + 1 = 2
x = 4 ⇒ y = \(\frac{1}{2}\) × 4 + 1 = 2 + 1 = 3
x = 6 ⇒ y = \(\frac{1}{2}\) × 6 + 1 = 3 + 1 = 4
x = – 2 ⇒ y = \(\frac{1}{2}\) × – 2 +1= – 1 + 1 = 0
x = – 4 ⇒ y = \(\frac{1}{2}\) × – 4 + 1 = – 2 + 1 = – 1
x = – 6 ⇒ y = \(\frac{1}{2}\) × – 6 + 1 = – 3 + 1 = – 2


The graph of y = \(\frac{1}{2}\)x + 1 stretches the graph y = x towards the x – axis since the multiplying factor is \(\frac{1}{2}\) which is less than 1 and shifts to the upward by 1 unit.

The graph of y = kf(x), k > 0 moves towards the x-axis if k is less than 1.
The graph of y = f(x) + d, d >0 causes the graph y = f(x) a shift to the upward by d units.

(v) 2x + y + 3 = 0
y = -2x – 3
When
x = 0 ⇒ y = -2 × 0 – 3 = -3
x = 1 ⇒ y = -2 × 1 – 3 = -5
x = \(\frac{1}{2}\) ⇒ y = – 2 × \(\frac{1}{2}\) – 3 = – 1 – 3 = – 4
x = 2 ⇒ y = -2 × 2 – 3 = – 4 – 3 = – 7
x = – 1 ⇒ y = -2 × – 1 – 3 = 2 – 3 = – 1
x = – 2 ⇒ y = 2 × – 2 – 3 = 4 – 3 = 1
x = – 3 ⇒ y = -2 × -3 – 3 = 6 – 3 = 3


The graph of y = – 2x – 3 stretches the graph y = x towards the x-axis since the multiplying factor is – 2 which is less than 1 and causes the shift to the downward by 3 units.5

The graph of y = kf(x), k > 0 moves towards the x-axis if k is less than 1.
The graph of y = f(x) – d, d >0 causes the graph y = f(x) a shift to the downward by d units.

Question 7.
From the curve y = |x| draw
(i) y = |x – 1| + 1
(ii) y = |x + 1| – 1
(iii) y = |x + 2| – 3
Answer:
y = |x|

(i) y = |x – 1| + 1
(a) Consider y = |x – 1|

x = 0 ⇒ y = – x + 1 ⇒ y = 1
x = 1 ⇒ y = x – 1 ⇒ y = 0
x = 2 ⇒ y = x – 1 ⇒ y = 1
x = 3 ⇒ y = x – 1 ⇒ y = 2
x = – 1 ⇒ y = – x + 1 ⇒ y = 2
x = – 2 ⇒ y = – x + 1 ⇒ y = 3

The graph of y = |x – 1| causes the graph y = |x| a shift to the right by 1 unit.

The graph of y = f(x – c), c > 0 causes the graph y = f(x) a shift to the right by c units.

(b) Consider y = |x – 1| + 1


x = 0 ⇒ y = – x + 2 ⇒ y = 2
x = 1 ⇒ y = x ⇒ y = 1
x = 2 ⇒ y = x ⇒ y = 2
x = 3 ⇒ y = x ⇒ y = 3
x = – 1 ⇒ y = – x + 2 ⇒ y = 3
x = – 2 ⇒ y = – x + 2 ⇒ y = 4

The graph of y = |x – 1| + 1 shift the graph y = |x| to the right by 1 unit and causes a shift to the upward by 1 unit.

The graph of y = f( x – c), c > 0 causes the graph y = f(x) a shift to the right by c units.
The graph of y = f(x) + d, d > 0 causes the graph y = f(x) a shift to the upward by d units.

(ii) y = |x + 1| – 1
(a) Consider y = |x + 1|

x = 0 ⇒ y = x + 1 ⇒ y = 1
x = 1 ⇒ y = x + 1 ⇒ y = 2
x = 2 ⇒ y = x + 1 ⇒ y = 3
x = 3 ⇒ y = x + 1 ⇒ y = 4
x = – 1 ⇒ y = x + 1 ⇒ y = 0
x = – 2 ⇒ y = – (x + 1) ⇒ y = 1
x = – 3 ⇒ y = – (x + 1) ⇒ y = 2

The graph of y = |x + 1| shifts the graph y = |x| to the left by 1 unit.

The graph of y = f( x + c), c > 0 causes the graph y = f(x) a shift to the left by e units.

(b) Consider y = |x + 1| – 1

x = 0 ⇒ y = x ⇒ y = 0
x = 1 ⇒ y = x ⇒ y = 1
x = 2 ⇒ y = x ⇒ y = 2
x = 3 ⇒ y = x ⇒ y = 3
x = – 1 ⇒ y = x ⇒ y = – 1
x = – 2 ⇒ y = – x – 2 ⇒ y = 0
x = – 3 ⇒ y = – x – 2 ⇒ y = 1
x = – 4 ⇒ y = – x – 5 ⇒ y = -1

The Graph of y = |x + 1 | – 1 shift the graph y = |x| to the left by 1 unit and causes a shift downward by 1 unit.

The graph of y = f(x + c), c > 0 causes the graph y = f(x) a shift to the left by c units.

The graph of y = f(x) – d, d > 0 causes the graph y = f(x) a shift to the downward by d units.

(iii) y = |x + 2| – 3
(a) Consider the curve y = |x + 2|

x = 0 ⇒ y = x + 2 ⇒ y = 2
x = 1 ⇒ y = x + 2 ⇒ y = 3
x = 2 ⇒ y = x + 2 ⇒ y = 4
x = 3 ⇒ y = x + 2 ⇒ y = 5
x = – 1 ⇒ y = x + 2 ⇒ y = 1
x = – 2 ⇒ y = x + 2 ⇒ y = 0
x = – 3 ⇒ y = – x – 2 ⇒ y = 1

The graph of y = |x + 2| shifts the graph y = |x| to the left by 2 units.

The graph of y = f(x + c), c > 0 causes the graph y = f(x) a shift to the left by c units.

(b) Consider the curve y = |x + 2| – 3

x = 0 ⇒ y = x – 1 ⇒ y = – 1
x = 1 ⇒ y = x – 1 ⇒ y = 0
x = 2 ⇒ y = x – 1 ⇒ y = 1
x = 3 ⇒ y = x – 1 ⇒ y = 2
x = – 1 ⇒ y = x – 1 ⇒ y = – 2
x = – 2 ⇒ y = x – 1 ⇒ y = – 3
x = – 3 ⇒ y = – x – 5 ⇒ y = – 2


The graph of y = |x + 2| – 3 shifts the graph y = |x| to the left by 2 units and causes a shift downward by 3 units.

The graph of y = f(x + c), c > 0 causes the graph y = f(x) a shift to the left by c units.
The graph of y = f(x) – d, d > 0 causes the graph y = f(x) a shift to the down ward by d units.

Question 8.
From the curve y = sin x, draw y = sin |x| (Hint: sin(- x) = – sin x)
Answer:
y = sin |x|
(a) y = sin x

(b) Consider y = sin |x|

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 Sets, Relations and Functions Ex 1.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets, Relations and Functions Ex 1.3

Question 1.
Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer.
Answer:
Given A denotes the set of students and B denotes the set of sections. Aslo given there 120 students and 4 sections.

Let f be a relation from A to B as “x related to y if the student x belongs to the section y”

Two are more students in A may belong to same section in B. But one student in A cannot belong to two or more sections in B. Every student in A can belong to any one of the section in B. Therefore / is a function.

In B we can have sections without students. Every element in B need not have preimage in A.
∴ f need not be onto.
Thus, f is a function and inverse relation for f need not exist.

Question 2.
Write the values of f at – 4, 1, -2, 7, 0 if

Answer:

When x = -4
f(x) = – x + 4
f(-4) = – (-4) + 4
= 4 + 4 = 8

When x = 1
f(x) = x – x²
f(1) = 1 – 1²
= 1 – 1 = 0

When x = -2
f(x) = x² – x
f(-2) = (-2)² – (-2)
= 4 + 2 = 6

When x – 7
f(x) = 0
⇒ f(7) = 0

When x = 0
f(x) = x² – x
⇒ f(0) = 0² – 0 = 0

Question 3.
Write the values of f at – 3, 5, 2, – 1, 0 if

Answer:

When x = – 3
f(x) = x² + x – 5
f(-3) = (-3)² + (-3) – 5
= 9 – 3 – 5
= 9 – 8 = 1

When x = 5
f(x) = x² + 3x – 2
f(5) = 5² + 3(5) – 2
= 25 + 15 – 2
= 40 – 2 = 38

When x = 2
f(x) = x² – 3
f(2) = 2² – 3 = 4 – 3 = 1

When x = – 1
f(x) = x² + x – 5
f(-1) = (-1)² – 1 – 5 = 1 – 1 – 5 = – 5

When x = 0
f(x) = x² – 3
f(0) = 0² – 3

Question 4.
State whether the following relations are functions or not. If it is a function, check for one – to – oneness and ontoness. If it is not a function, state why?
(i) If A = { a, b, c } and f = { (a, c), (b, c), (c, b) }; (f : A → A)
Answer:
A = { a, b, c }
f = {(a, c), (b, c), (c, b)}; f : A → A

f is a function since every element in the domain has a unique image in the codomain.
f is not one-one.
a, b belonging to the domain A has the same image in the codomain A. f is not onto since belonging to the codomain A does not have preimage in the domain A Thus the relation / is a function from A to A and it is neither one-one nor onto.

(ii) If X = { x, y, z } and f = { (x, y), (x, z), (z, x) }; (f: X → X)
Answer:
X = { x, y, z }
f = {(x, y), (x, z), (z , x) } f : X → X

The relation f: X → X is not a function since the element x in the domain has two images in the co-domain.

Question 5.
Let A = {1, 2, 3, 4} and B = { a, b , c, d } Give a function from A → B for each of the following.
(i) neither one-to-one nor onto.
Answer:

f = { (1, b) , (2, c) , (3, d) , (4, d)
f is a function, it not one to one and not onto.

(ii) not one – to – one but onto
Answer:
Does not exists

(iii) one – to – one but not onto
Answer:
Does not exist

(iv) one – to – one and onto
Answer:

f = { (1, a) , (2, b) , (3, c) , (4, d) }
f is a function which is one – to – one and onto.

Question 6.
Find the domain of \(\frac{1}{1-2 \sin x}\)
Answer:
Let f(x) = \(\frac{1}{1-2 \sin x}\)
When 1 – 2 sin x = 0
⇒ 1 = 2 sin x
sin x = \(\frac{1}{2}\)
⇒ sin x = sin \(\left(\frac{\pi}{6}\right)\)
x = nπ + (- 1)ⁿ\(\frac{\pi}{6}\), n ∈ Z
sin x = sin α ⇒ x = nπ + (-1)ⁿd, n ∈ Z
∴ Domain of f(x) is

Question 7.
Find the largest possible domain of the real valued function f(x) = \(\frac{\sqrt{4-x^{2}}}{\sqrt{x^{2}-9}}\)
Answer:

∴ For no real values of x, f (x) is defined.
∴ Domain of f(x) = { }

Question 8.
Find the range of the function \(\frac{1}{2 \cos x-1}\)
Answer:
Let f(x) = \(\frac{1}{2 \cos x-1}\)
Range of cosine function is
– 1 ≤ cos x ≤ 1
– 2 ≤ 2 cos x ≤ 2
– 1 ≤ 2 cos x – 1 ≤ 2 – 1
– 3 ≤ 2 cos x – 1 ≤ 1
\(-\frac{1}{3}\) ≥ \(\frac{1}{2 \cos x-1}\) ≥ 1

Question 9.
Show that the relation xy = – 2 is a function for a suitable domain. Find the domain and the range of the function.
Answer:
xy = – 2 ⇒ y = -2/x
which is a function
The domain is (-∞, 0) ∪ (0, ∞) and range is R – {0}

Question 10.
If f, g : R → R are defined by f(x) = |x| + x and g(x) = |x| – x find gof and fog.
Answer:
Given

Question 11.
If f, g, h are real-valued functions defined on R, then prove that (f + g)oh = foh + goh what can you say about fo(g + h )? Justify your answer.
Answer:
Given f : R → R , g : R → R and h : R → R (f + g) oh: R → R and (f o h + g o h) : R → R for any x ∈ R.
[(f + g)oh] (x) = (f + g) h(x)
= f(h(x)) + g(h(x))
= foh(x) + goh(x)
∴ (f + g)oh = foh + goh
Also fo(g + h)(x) = f((g + h)(x)) for any x ∈ R
= f(g(x) + h(x))
= f(g(x)) + f(h(x))
= fog (x) + foh(x)
∴ fo(g + h) = fog +foh

Question 12.
If f : R → R is defined by f( x ) = 3x – 5, Prove that f is a bijection and find its inverse.
Answer:
Given f(x) = 3x – 5
Let y = 3x – 5
y + 5 = 3x
⇒ \(\frac{y+5}{3}\) = x
Let g(y) = \(\frac{y+5}{3}\)
gof (x) = g(f(x))
= g(3x – 5)
= \(\frac{3 x-5+5}{3}\) = \(\frac{3 x}{3}\) = x
gof (x) = x
fog (y) = f(g(y))
= f\(\left(\frac{y+5}{3}\right)\)
= 3\(\left(\frac{y+5}{3}\right)\) – 5
= y + 5 – 5
fog(y) = y
∴ gof = I_x and fog = I_Y
Hence f and g are bijections and inverses to each ot1er.
Hence f is a bijection and f^-1(y) = \(\frac{y+5}{3}\)
Replacing y by x we get f^-1(x) = \(\frac{x+5}{3}\)

Question 13.
The weight of the muscles of a man is a function of his bodyweight x and can be expressed as W ( x ) = 0.35x. Determine the domain of this function.
Answer:
W(x) = 0.35x
Since bodyweight x is positive and if it increases then W(x) also increases.
Domain is (0, ∞) i.e.,x > 0

Question 14.
The distance of an object falling is a function of time t and can be expressed as s ( t) = – 16t². Graph the function and determine if it is one – to – one.
Answer:
Given s (t) = – 16t²
s (t₁) = s (t₂) ⇒ – 16t₁² = – 16t₂²
⇒ t₁² = t₂²
⇒ ± t₁ = ± t₂
Since s (t₁) = s (t₁) 14 t₁ = t₂
∴ The function s(t) is not one-one
Graph of s(t) = – 16t²
Take the time along x – axis and distance along y – axis.

Question 15.
The total cost of airfare on a given route is comprised of the base cost C and the fuel Surcharge S in rupee. Both C and S are functions of the mileage m; C ( m ) = 0.4 m + 50 and S ( m ) = 0.03m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.
Answer:
C – base cost,
S = fuel surcharge,
m = mileage
C(m) = 0.4 m + 50
S(m) = 0.03 m
Total cost = C(m) + S(m)
= 0.4 m + 50 + 0.03 m
= 0.43 m + 50
for 1600 miles
T(c) = 0.43 (1600) + 50 = 688 + 50 = ₹ 738

Question 16.
A salesperson whose annual earnings can be represented by the function A (x) = 30,000 + 0.04 x, where x is the rupee value of the merchandise, he sells. His son is also in sales and his earnings are represented by the function S(x) = 25,000 + 0.05 x. Find (A + S)(x) and determine the total family income if they each sell Rs. 1,50,00,000 worth of merchandise.
Answer:
Given A (x) = 30,000 + 0.04 x
S (x) = 25,000 + 0.05x
A(x) + S(x) = 30,000 + 0.04 x + 25,000 + 0.05x
(A + S)(x) = 55,000 + 0.09 x
Given x = 1,50,00,000
Then (A + S)(x) = 55000 + 0.09 × 1,50,00,000
= 55000 + 1,35000000
Total family income = Rs. 14,05,000

Question 17.
The function for exchanging American dollars for Singapore Dollar on a given day is f (x) = 1.23x, where x represents the number of American dollars. On the same day, the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee.
Answer:
Given f(x) = 1.23x
where x represents the number of American dollars
g(y) = 50.50y
where y represents the number of Singapore dollars.

To convert American dollars to Indian rupees, we must find
gof (x) = g(f(x))
= g (1.23x)
= 50.50 (1.23x)
= 62.115x
∴ The function for the exchange rate of American can dollars in terms of Indian rupees is
gof (x) = 62.1 15x

Question 18.
The owner of a small restaurant can prepare a particular meal at a cost of Rs. 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D (x) = 200 – x. Express his day revenue total cost and profit on this meal as functions of x.
Answer:
cost of one meal = ₹ 100
Total cost = ₹ 100 (200 – x)
Number of customers = 200 – x
Day revenue = ₹ (200 – x) x
Total profit = day revenue – total cost
= (200 – x) x – (100) (200 – x)

Question 19.
The formula for converting from Fahrenheit to Celsius temperature is y = \(\). Find the inverse of this function and determine whether the inverse is also a function?
Answer:

Question 20.
A simple cipher takes a number and codes it, using the function f( x) = 3x – 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x (by drawing the lines)
Answer:
Given f(x) = 3x – 4
Let y = 3x – 4
⇒ y + 4 = 3x
⇒ x = \(\frac{y+4}{3}\)
Let g(y) = \(\frac{y+4}{3}\)
gof (x) = g (f(x) )
= g(3x – 4)
= \(\frac{3 x-4+4}{3}=\frac{3 x}{3}\)
gof(x) = x
and fog(y) = f(g(y))
= f\(\left(\frac{y+4}{3}\right)\)
= 3\(\left(\frac{y+4}{3}\right)\)
= y + 4 – 4 = y
fog (y) = y
Hence g of = I_x and fog = I_y
This shows that f and g are bijections and inverses of each other.
Hence f is bijection and f^-1(y) = \(\frac{y+4}{3}\)
Replacing y by x we get f^-1(x) = \(\frac{x+4}{3}\)
The line y = x

f(x) =
The line y =3x-4
When x = 0 ⇒ y = 3 × 0 – 4 = -4
When x = 1 ⇒ y = 3 × 1 – 4 = -1
When x = -1 ⇒ y = 3 × -1 – 4 = -7
When x = 2 ⇒ y = 3 × 2 – 4 = 2
When x = -2 ⇒ y = 3 × -2 – 4 = -10
When x = 3 ⇒ y = 3 × 3 – 4 = 5
When x = -3 ⇒ y = 3 × -3 – 4 = -13

The line y = \(\frac{x+4}{3}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 Sets, Relations and Functions Ex 1.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets, Relations and Functions Ex 1.2

Question 1.
Discuss the following relations for reflexivity, symmetricity and transitivity:
(i) The relation R defined on the set of all positive integers by “m R n if m divides n”.
(ii) Let P denote the set of all straight lines in a plane. The relation R defined by “ l R m if l is perpendicular to m”.
(iii) Let A be the set consisting of all the members of a family. The relation R defined by “a R b if a is not a sister of b”.
(iv) Let A be the set consisting of all the female members of a family. The relation R defined by “a R b if a is not a sister of b”.
(v) On the set of natural numbers the relation R defined by “x R y if x + 2y = 1”

(i) The relation R defined on the set of all positive integers by “m R n if m divides n”.
Answer:
S = {set of all positive integers}

(a) mRm ⇒ ‘m’ divides’m’ ⇒ reflexive

(b) mRn ⇒ m divides n but
nRm ⇒ n does not divide m
(i.e.,) mRn ≠ nRm
It is not symmetric

(c) mRn ⇒ nRr as n divides r
It is transitive

(ii) Let P denote the set of all straight lines in a plane. The relation R defined by“ l R m if l is perpendicular to m”.
Answer:
Let P denote the set of all straight lines in a plane. The relation R is defined by l R m if l is perpendicular to m.
R = {(l, m): l is perpendicular to m}

(a) Reflexive:
Let l be any line in the plane P. Then line l is not perpendicular to itself.
{1, 1) ∉ R
∴ R is not reflexive.

(b) Symmetric:
Let (1, m) ∉ R ⇒ l is perpendicular to m
∴ m is perpendicular to l.
Hence (m, l) ∈ R
∴ R is symmetric.

(c) Transitive;
Let (l, m), (m, n) ∈ R
⇒ l is perpendicular to m.
∴ l is parallel to n. (l , n) ∉ R
Hence R is not transitive.

(iii) Let A be the set consisting of all the members of a family. The relation R defined by “a R b if a is not a sister of b”.
Answer:
A = {set of all members of the family}
aRb is a is not a sister of b

(a) aRa ⇒ a is not a sister of a It is reflexive

(b) aRb ⇒ a is not a sister of b.
bRa ⇒ b is not a sister of a.
It is symmetric

(c) aRb ⇒ a is not a sister of b.
bRc ⇒ b is not a sister of c.
⇒ aRc ⇒ a can be a sister of c
It is not transitive.

(iv) Let A be the set consisting of all the female members of a family. The relation R defined by “a R b if a is not a sister of b”.
Answer:
Given A is the set containing female members of the family.
Let M = Mother
H = Female child
A = { M, H }
The relation R on A is defined by aRb if a is not a sister of b.
R = {(M, M), (M, H), (H, H), (H, M)}

(a) Reflexive:
Clearly (M, M) and (H, H) ∈ R.
∴ R is reflexive.

(b) Symmetric:
For (M, H) ∈ R, we have (H, M ) ∈ R
∴ R is symmetric.

(c) Transitive:
For (M,M),(M,H) ∈ R ⇒ (M, H) ∈ R
(M,H),(H,H) ∈ R ⇒ (M, H) ∈ R
(H,H),(H,M) ∈ R ⇒ (H, M) ∈ R
(H,M),(M,M) ∈ R ⇒ (H, M) ∈ R
(H,M),(M,H) ∈ R (H, H) ∈ R
∴ R is transitive.

(v) On the set of natural numbers the relation R defined by “x R y if x + 2y = 1”
Answer:
N= {1, 2, 3, 4, 5,….}
xRy if x + 2y = 1 R is an empty set

(a) xRx ⇒ x + 2x = 1 ⇒ x = \(\frac{1}{3}\) ∉ N. It is not reflexive
xRy = yRx ⇒ x + 2y = 1 It does not imply that y + 2x = 1 as y = \(\frac{1-x}{2}\) It is not symmetric.

(b) -x = y ⇒ (-1, 1) ∉ N
It is not transitive.

Question 2.
Let X = { a , b , c , d } and R = { (a, a ) , (b, b ), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence
Answer:
Given X = { a, b, c, d }
R = { (a, a), (b, b), (a, c) }
(i) The minimum ordered pairs to be included to R in order to make R to be reflexive is (c, c) and (d, d)
(ii) The minimum ordered pairs to be included to R in order to make R to be symmetric is (c, a).
(iii) R is transitive. We need not add any pair.
(iv) After adding the ordered pairs (c, c),(d, d), (c, a) the new relation becomes
R, = {(a, a), (b, b), (c, c), (d, d), (a, c), (c, a)}
The new relation satisfies, reflexive, symmetric and transitive property.
∴ R₁ is an equivalence relation.

Question 3.
Let A = { a, b , c } and R = { (a, a ) , (b, b ), (a, c ) }. Write down the minimum number of ordered pairs to be included to R to make it
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence
Answer:
Given A = {a, b, c }
R = { (a, a), (b, b),(a, c) }
(i) The minimum ordered pair to be included to R in order to make it reflexive is (c, c).
(ii) The minimum ordered pair to be included to R in order to make it symmetrical is (c, a).
(iii) R is transitive. We need not add any pair.
(iv) After including the ordered pairs (c, c),(c, a) to R the new relation becomes
R₁ = { (a, a), (b, b), (c, c) , (a, c) , (c, a) }
R₁ is reflexive symmetric and transitive.
∴ R₁ is an equivalence relation.

Question 4.
Let P be the set of all triangles in a plane and R be the relation defined on P as a R b if a is similar to b. Prove that R is an equivalence relation.
Answer:
Given P = the set of all triangles in a plane.
R is the relation defined by a R b if a is similar to b.
R = {(a, b) : a is similar to b for a, b ∈ p }

(a) Reflexive:
(a, a) ⇒ a is similar to a for all a ∈ P
∴ R is reflexive.

(b) Symmetric: .
Let (a,b) ∈ R ⇒ a is similar to b
⇒ b is similar to a
∴ (b, a) ∈ R
Hence R is symmetric.

c) Transitive:
Let (a, b) and ( b, c) ∈ R
(a, b) ∈ R ⇒ a is similar to b
(b, c) ∈ R ⇒ b is similar to c
∴ a is similar to c.
Hence R is transitive.
∴ R is an equivalence relation on P.

Question 5.
On the set of natural numbers let R be the relation defined by a R b if 2a + 3b = 30. Write down the relation by listing all the pairs. Cheek whether it is
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence
Answer:
Given N = set of natural numbers
R is the relation defined by a R b if 2a + 3b = 30


When a > 15, b negative and does not belong to N.
∴ R = { (3,8),(6,6), (9,4), (12,2)}.
(i) R is not reflexive since (a, a) ∉ R for all a ∈ N.
(ii) R is not symmetric since for (3, 8) ∈ R, (8, 3) ∉ R
(iii) Clearly R is transitive since we cannot find elements (a, b), (b, c) in R such that (a, c) ∉ R
∴ R is not an equivalence relation.

Question 6.
Prove that the relation ‘friendship’ is not an equivalence relation on the set of all people in Chennai.
Answer:
(a) S = aRa (i.e. ) a person can be a friend to himself or herself.
So it is reflective.

(b) aRb ⇒ bRa so it is symmetric

(c) aRb, bRc does not ⇒ aRc so it is not transitive
⇒ It is not an equivalence relation

Question 7.
On the set of natural numbers let R be the relation defined by a R b if a + b < 6. Write down the relation by listing all the pairs. Check whether it is
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence.
Answer:
N = the set of natural numbers.
R is the relation defined on N by
a R b if a + b ≤ 6
R = { (a, b), a, b ∈ N / a + b ≤ 6}
a + b ≤ 6 ⇒ b ≤ 6 – a

a = 1,
b ≤ 6 – 1 = 5
b is 1, 2, 3, 4, 5
∴ (1, 1), (1, 2), (1, 3), (1, 4), (1, 5) ∈ R

a = 2,
b ≤ 6 – 2 = 4
b is 1, 2, 3, 4
∴ (2, 1), (2, 2),(2, 3), (2, 4) ∈ R

a = 3,
b < 6 – 3 = 3
b is 1, 2, 3
∴ (3, 1), (3, 2), (3, 3) ∈ R

a = 4 ,
b < 6 – 4 = 2
b is 1, 2
∴ (4, 1), (4, 2) ∈ R

a = 5,
b < 6 – 5 = 1
b is 1
∴ (5, 1) ∈ R
∴ R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (5, 1)}

(i) Reflexive:
R is not reflexive since (4, 4), (5, 5) ∈ R

(ii) Symmetric:
Cleary R is symmetric forever (x, y) ∈ R, we have (y, x) ∈ R.

(iii) Transitive:
(3, 1), (1, 5) ∈ R ⇒ (3,5) ∉ R
∴ R is not transitive.

(iv) R is not an equivalence relation.

Question 8.
Let A = { a, b, c }. What is the equivalence relation of smallest cardinality on A? What is the equivalence relation of largest cardinality on A?
Answer:
R = {{a, a), (b, b), (c, c)} is this smallest cardinality of A to make it equivalence relation n(R) = 3

(i) R = {(a, a), {a, b), (a, c), (b, c), (b, b), {b, c), (c, a), (c, b), (c, c)}
n(R) = 9 is the largest cardinality of R to make it equivalence.

Question 9.
In the set Z of integers, define m Rn if m – n is divisible by 7. Prove that R is an equivalence relation.
Answer:
Z = set of all integers
Relation R is defined on Z by m R n if m – n is divisible by 7.
R = {(m, n), m, n ∈ Z/m – n divisible by 7}
m – n divisible by 7
∴ m – n = 7k where k is an integer.

a) Reflexive:
m – m = 0 = 0 × 7
m – m is divisible by 7
∴ (m, m ) ∈ R for all m ∈ Z
Hence R is reflexive.

b) Symmetric:
Let (m, n ) ∈ R ⇒ m – n is divisible by 7
m – n = 7k
n – m = – 7k
n – m = (-k)7
∴ n – m is divisible by 7
∴ (n, m) ∈ R.

c) Transitive:
Let (m, n) and (n , r) ∈ R
m – n is divisible by 7
m – n = 7k ——— (1)
n – r is divisible by 7
n – r = 7k₁ ——— (2)
(m – n) + (n – r) = 7k + 7k₁
m – r = ( k + k₁) 7
m – r is divisible by 7.
∴ (m, r) ∈ R
Hence R is transitive.
R is an equivalence relation.