Tamilnadu State Board New Syllabus Samcheer Kalvi 11th Business Maths Guide Pdf Chapter 7 Financial Mathematics Ex 7.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 7 Financial Mathematics Ex 7.1
Samacheer Kalvi 11th Business Maths Financial Mathematics Ex 7.1 Text Book Back Questions and Answers
Question 1.
Find the amount of an ordinary annuity of ₹ 3,200 per annum for 12 years at the rate of interest of 10% per year, [(1.1)12 = 3.1384]
Solution:
Here a = 3,200, n = 12, and i = \(\frac{10}{100}\) = 0.1
A = \(\frac{a}{i}\) [(1 + i)n – 1]
= \(\frac{3200}{0.1}\) [(1 + 0.1)12 – 1]
= 32000 [(1.1)12 – 1]
= 32000 [3.1384 – 1] [∵ (1.1)12 = 3.1384]
= 32000 [2.1384]
= ₹ 68,428.8
![]()
Question 2.
If the payment of ₹ 2,000 is made at the end of every quarter for 10 years at the rate of 8% per year, then find the amount of annuity. [(1.02)40 = 2.2080]
Solution:
Here a = 2,000, n = 10 years, and \(\frac{i}{k}=\frac{\frac{8}{100}}{4}=\frac{2}{100}=0.02\)
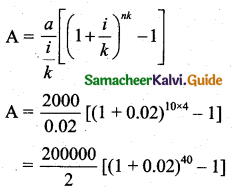
= 100000 [2.2080 – 1] [∵ (1.02)40 = 2.2080]
= 100000 [1.2080]
= ₹ 1,20,800
Question 3.
Find the amount of an ordinary annuity of 12 monthly payments of ₹ 1,500 that earns interest at 12% per annum compounded monthly. [(1.01)12 = 1.1262]
Solution:
Here a = 1,500, n = 1 year, and i = \(\frac{12}{100}\)

= 150000 [(1.01)12 – 1]
= 150000 [1.1262 – 1] (∵ (1.01)12 = 1.1262)
= 150000 [0.1262]
= ₹ 18,930
![]()
Question 4.
A bank pays 8% per annum interest compounded quarterly. Find equal deposits to be made at the end of each quarter for 10 years to have ₹ 30,200? [(1.02)40 = 2.2080]
Solution:
Here A = ₹ 30200, i = \(\frac{8}{100}\)

Question 5.
A person deposits ₹ 2,000 from his salary towards his contributory pension scheme. The same amount is credited by his employer also. If an 8% rate of compound interest is paid, then find the maturity amount at end of 20 years of service. [(1.0067)240 = 4.966]
Solution:
A person deposit ₹ 2,000.
The employer also credited the same amount.
a = ₹ 2,000 + ₹ 2,000 = ₹ 4,000

Note:
If (1.0067) = 4.966 (Original value)
Then A = 600000 (4.966 – 1)
= 600000(3.966)
= ₹ 23,79,600
![]()
Question 6.
Find the present value of ₹ 2,000 per annum for 14 years at the rate of interest of 10% per annum. [(1.04)-14 = 0.6252]
Solution:
Here a = 2000, n = 14, and i = \(\frac{10}{100}\) = 0.1
\(P=\frac{a}{i}\left[1-\frac{1}{(1+i)^{n}}\right]\)
= \(\frac{2000}{0.1}\left[1-\frac{1}{(1+0.1)^{14}}\right]\)
= \(\frac{2000}{0.1}\left[1-(1.1)^{-14}\right]\)
= 20000 [1 – 0.2632]
= 20000 × 0.73678
= ₹ 14,735.60
Question 7.
Find the present value of an annuity of ₹ 900 payable at the end of 6 months for 6 years. The money compounded at 8% per annum. [(1.04)-12 = 0.6252]
Solution:
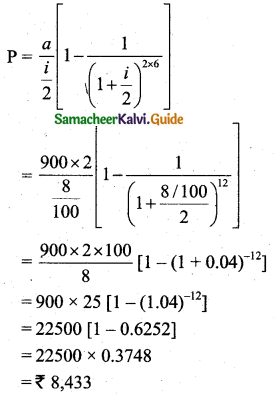
![]()
Question 8.
Find the amount at the end of 12 years of an annuity of ₹ 5,000 payable at the beginning of each year, if the money is compounded at 10% per annum.
Solution:
Here a = 5000, i = 10% = \(\frac{10}{100}\) = 0.1, n = 12
Amount A = (1 + i) \(\frac{a}{i}\) [(1 + i)n – 1]
= (1 + 0.1) \(\frac{5000}{\frac{10}{100}}\) [(1 + 0.1)12 – 1]
= (1.1) 50000 [(1.1)12 – 1]
= 55000 [3.1384 – 1]
= 55000 [2.1384]
= ₹ 1,17,612
Question 9.
What is the present value of an annuity due of ₹ 1,500 for 16 years at 8% per annum? [(1.08)15 = 3.172]
Solution:
Present value of annuity due, \(\mathrm{P}=\frac{a(1+i)}{i}\left[1-\frac{1}{(1+i)^{n}}\right]\)
Here a = 1500, n = 16, i = \(\frac{8}{100}\) = 0.08

= 18750[1.08 – \(\frac{1}{3.1721}\)] [∵ (1.08)15 = 3.1721]
= 18750[1.08 – 0.31524]
= 18750[0.7648]
= ₹ 14340
![]()
Question 10.
What is the amount of perpetual annuity of ₹ 50 at 5% compound interest per year?
Solution:
\(P=\frac{a}{i}=\frac{50}{\left(\frac{5}{100}\right)}=\frac{50 \times 100}{5}=₹ 1,000\)