Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.4
Choose the most suitable answer from the given four alternatives:
Question 1.
Area bounded by the curve y = x (4 – x) between the limits 0 and 4 with x-axis is
(a) \(\frac { 30 }{3}\) sq.unit
(b) \(\frac { 31 }{2}\) sq.unit
(c) \(\frac { 32 }{3}\) sq.unit
(d) \(\frac { 15 }{3}\) sq.unit
Solution:
(c) \(\frac { 32 }{3}\) sq.unit
Hint:
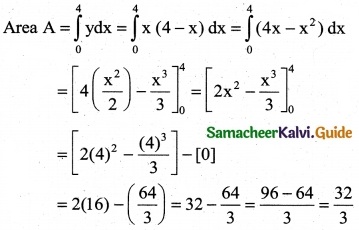
![]()
Question 2.
Area bounded by the curve y = e-2x between the limits 0 < x < ∞ is
(a) 1 sq.units
(b) \(\frac { 1 }{2}\) sq.units
(c) 5 sq.units
(d) 2 sq.units
Solution:
(b) \(\frac { 1 }{2}\) sq.units
Hint:
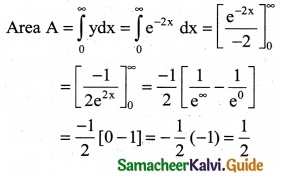
Question 3.
Area bounded by the curve y = \(\frac { 1 }{x}\) between the limits 1 and 2 is
(a) log 2 sq.units
(b) log 5 sq.units
(c) log 3 sq.units
(d) log 4 sq.units
Solution:
(a) log 2 sq.units
Hint:
Area = \(\int_{1}^{2} \frac{1}{x} d x\)
= \((\log x)_{1}^{2}\)
= log 2 – log 1
= log 2 (Since log 1 = 0)
![]()
Question 4.
If the marginal revenue function of a firm is MR = e\(\frac { -x }{10}\) then revenue is
(a) 1 – e-x/10
(b) e-x/10 + 10
(c) 10(1 – e-x/10)
(d) -10e-x/10
Solution:
(c) 10(1 – e-x/10)
Hint:
MR = e\(\frac { -x }{10}\) then R = ∫MR dx
R = ∫e-x/10 dx = \(\frac { e^{-x/10} }{(-1/10)}\) + k
R = -10e-x/10 + k when x = 0, R = 0
⇒ 0 = -10e0 + k
0 = -10(1) + k
∴ k = 10
R = -10e-x/10 + 10 = 10(1 – e-x/10)
Question 5.
If MR and MC denotes the marginal revenue and marginal cost functions, then the profit functions is
(a) P = ∫(MR – MC) dx + k
(b) P = ∫(R – C) dx + k
(c) P = ∫(MR + MC)dx + k
(d) P = ∫(MR) (MC) dx + k
Solution:
(a) P = ∫(MR – MC) dx + k
Hint:
Profit = Revenue – Cost
Question 6.
The demand and supply functions are given by D(x) = 16 – x² and S(x) = 2x² + 4 are under perfect competition, then the equilibrium price x is
(a) 2
(b) 3
(c) 4
(d) 5
Solution:
(a) 2
Hint:
D(x) =16 – x² and S(x) = 2x² + 4
Under perfect competition D(x) = S(x)
16 – x² = 2x² + 4; 16 – 4 = 2x² + x²
3x² = 12 ⇒ x² = \(\frac { 12 }{3}\) = 4
∴ x = ± 2, x cannot be in negative
∴ x = 2
![]()
Question 7.
The marginal revenue and marginal coast functions of a company are MR = 30 – 6x and MC = -24 + 3x where x is the product, profit function is
(a) 9x² + 54x
(b) 9x² – 54x
(c) 54x – \(\frac { 9x^2 }{2}\)
(d) 54x – \(\frac { 9x^2 }{2}\) + k
Solution:
(d) 54x – \(\frac { 9x^2 }{2}\) + k
Hint:
Profit = ∫(MR – MC) dx + k
= ∫(30 – 60) – (-24 + 3x) dx + k
= ∫(54 – 9x) dx + k
= 54x – \(\frac{9 x^{2}}{2}\) + k
Question 8.
The given demand and supply function are given by D(x) = 20 – 5x and S(x) = 4x + 8 if they are under perfect competition then the equilibrium demand is
(a) 40
(b) \(\frac { 41 }{2}\)
(c) \(\frac { 40 }{3}\)
(d) \(\frac { 41 }{5}\)
Solution:
(c) \(\frac { 40 }{3}\)
Hint:
Under perfect competition D(x) = S(x)
20 – 5x = 4x + 8
20 – 8 = 4x + 5x ⇒ 9x = 12
x = \(\frac { 4 }{3}\)
when x = \(\frac { 4 }{3}\); D(x) = 20 – 5(\(\frac { 4 }{3}\)) = 20 – \(\frac { 20 }{3}\)
= \(\frac { 40 }{3}\)
Question 9.
If the marginal revenue MR = 35 +7x – 3x², then the average revenue AR is.
(a) 35x + \(\frac { 7x^2 }{2}\) – x³
(b) 35x + \(\frac { 7x }{2}\) – x²
(c) 35x + \(\frac { 7x }{2}\) + x²
(d) 35x + 7x + x²
Solution:
(c) \(\frac { 40 }{3}\)
Hint:
R = ∫MR dx = ∫(35 + 7x – 3x²) dx
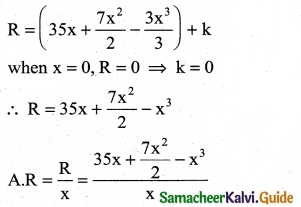
![]()
Question 10.
The profit of a function p(x) is maximum when
(a) MC – MR = 0
(b) MC = 0
(c) MR = 0
(d) MC + MR = 0
Solution:
(a) MC – MR = 0
Hint:
P = Revenue – Cost
P is maximum when \(\frac{d p}{d x}\) = 0
\(\frac{d p}{d x}\) = R'(x) – C'(x) = MR – MC = 0
Question 11.
For the demand function p(x), the elasticity of demand with respect to price is unity then.
(a) revenue is constant
(b) a cost function is constant
(c) profit is constant
(d) none of these
Solution:
(a) Revenue is constant
Question 12.
The demand function for the marginal function MR = 100 – 9x² is
(a) 100 – 3x²
(b) 100x – 3x²
(c) 100x – 9x²
(d) 100 + 9x²
Solution:
(a) 100 – 3x²
Hint:
R = ∫(MR) dx + c1
R = ∫(100 – 9x2) dx + c1
R = 100x – 3x3 + c1
When R = 0, x = 0, c1 = 0
R = 100x – 3x3
Demand function is \(\frac{R}{x}\) = 100 – 3x2
![]()
Question 13.
When x0 = 5 and p0 = 3 the consumer’s surplus for the demand function pd = 28 – x²
(a) 250 units
(b) \(\frac { 250 }{3}\) units
(c) \(\frac { 251 }{2}\) units
(d) \(\frac { 251 }{3}\) units
Solution:
(b) \(\frac { 250 }{3}\) units
Hint:

Question 14.
When x0 = 2 and P0 = 12 the producer’s surplus for the supply function P0 = 2x² + 4 is
(a) \(\frac { 31 }{5}\) units
(b) \(\frac { 31 }{2}\) units
(c) \(\frac { 32 }{2}\) units
(d) \(\frac { 30 }{7}\) units
Solution:
(c) \(\frac { 32 }{2}\) units
Hint:
Producer’s Surplus

Question 15.
Area bounded by y = x between the lines y = 1, y = 2 with y = axis is
(a) \(\frac { 1 }{2}\) sq units
(b) \(\frac { 5 }{2}\) sq units
(c) \(\frac { 3 }{2}\) sq units
(d) 1 sq units
Solution:
(c) \(\frac { 3 }{2}\) sq units
Hint:
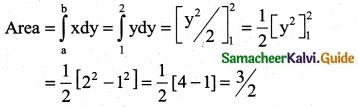
![]()
Question 16.
The producer’s surplus when supply the function for a commodity is p = 3 + x and x0 = 3 is
(a) \(\frac { 1 }{2}\)
(b) \(\frac { 9 }{2}\)
(c) \(\frac { 3 }{2}\)
(d) \(\frac { 7 }{2}\)
Solution:
(b) \(\frac { 9 }{2}\)
Hint:
p = 3 + x and x0 = 3
then p0 = 3 + 3 = 6

Question 17.
The marginal cost function is MC = 100√x find AC given that TC = 0 when the out put is zero is
(a) \(\frac { 200 }{3}\) x1/2
(b) \(\frac { 200 }{3}\) x3/2
(c) \(\frac { 200 }{3x^{3/2}}\)
(d) \(\frac { 200 }{3x^{1/2}}\)
Solution:
(a) \(\frac { 200 }{3}\) x1/2
Hint:
TC = ∫MC dx = ∫100√x dx = 100 ∫(x)1/2 dx

Question 18.
The demand and supply function of a commodity are P(x) = (x – 5)² and S(x) = x² + x + 3 then the equilibrium quantity x0 is
(a) 5
(b) 2
(c) 3
(d) 10
Solution:
(b) 2
Hint:
At equilibrium, P(x) = S(x)
⇒ (x – 5)2 = x2 + x + 3
⇒ x2 – 10x + 25 = x2 + x + 3
⇒ 11x = 22
⇒ x = 2
![]()
Question 19.
The demand and supply function of a commodity are D(x) = 25 – 2x and S(x) = \(\frac { 10+x }{2}\) then the equilibrium price P0 is
(a) 2
(b) 2
(c) 3
(d) 10
Solution:
(a) 2
Hint:
At equilibrium, D(x) = S(x)
25 – 2x = \(\frac{10+x}{4}\)
⇒ 100 – 8x = 10 + x
⇒ x = 10
That is x0 = 10
P0 = 25 – 2(x0) = 25 – 20 = 5
Question 20.
If MR and MC denote the marginal revenue and marginal cost and MR – MC = 36x – 3x² – 81, then maximum profit at x equal to
(a) 3
(b) 6
(c) 9
(d) 10
Solution
(c) 9
Hint:
Profit P = ∫(MR – MC) dx = ∫(36x – 3x² – 81) dx
P = [\(\frac { 36x^2 }{2}\) – \(\frac { 3x^3 }{3}\) – 81x] = 18x² – x³ – 81x
when p = 0; 18x² – x³ – 81x = 0 ⇒ x² – 18x + 81 = 0
(x – 9)² = 0 ⇒ x – 9 = 0
∴ x = 9
Question 21.
If the marginal revenue of a firm is constant, then the demand function is
(a) MR
(b) MC
(c) C(x)
(d) AC
Solution:
(a) MR
Hint:
MR = k (constant)
Revenue function R = ∫(MR) dx + c1
= ∫kdx + c1
= kx + c1
When R = 0, x = 0, ⇒ c1 = 0
R = kx
Demand function p = \(\frac{R}{x}=\frac{k x}{x}\) = k constant
⇒ p = MR
![]()
Question 22.
For a demand function p, if ∫\(\frac { dp }{p}\) = k ∫\(\frac { dx }{x}\) then k is equal to
(a) nd
(b) -nd
(c) \(\frac { -1 }{n_d}\)
(d) \(\frac { 1 }{n_d}\)
Solution:
(c) \(\frac { -1 }{n_d}\)
Question 23.
The area bounded by y = ex between the limits 0 to 1 is
(a) (e – 1) sq.units
(b) (e + 1) sq.units
(c) (1 – \(\frac { 1 }{e}\)) sq.units
(d) (1 + \(\frac { 1 }{e}\)) sq.units
Solution:
(a) (e – 1) sq.units
Hint:
Area A = \(\int_{a}^{b}\)ydx = \(\int_{0}^{1}\)exdx = [ex]\(_{0}^{1}\)
= [ex – e°] = [e – 1]
Question 24.
The area bounded by the parabola y² = 4x bounded by its latus rectum is
(a) \(\frac { 16 }{3}\) sq units
(b) \(\frac { 8 }{3}\) sq units
(c) \(\frac { 72 }{3}\) sq units
(d) \(\frac { 1 }{3}\) sq units
Solution:
(b) \(\frac { 8 }{3}\) sq units
Hint:
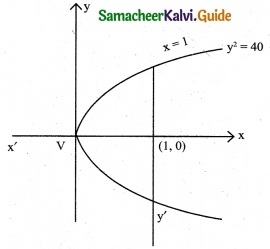
y² = 4x ⇒ y = \(\sqrt { 4x}\) 2√x = 2(x)1/2
In this parabola 4a = 4 ⇒ a = 1 and vertex V(0, 0)
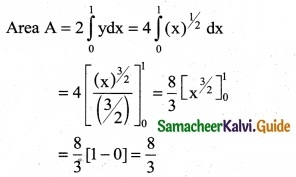
![]()
Question 25.
The area bounded by y = |x| between the limits 0 and 2 is
(a) 1 sq.units
(b) 3 sq.units
(c) 2 sq.units
(d) 4 sq.units
Solution:
(c) 2 sq.units
Hint:
Area A = \(\int_{a}^{b}\)ydx = \(\int_{0}^{2}\)x dx = [ \(\frac { x^2 }{2}\) ]\(_{0}^{2}\)
= \(\frac { (2)^2 }{2}\) – (0) = \(\frac { 4 }{2}\) = 2
Must Read: