Students can download Maths Chapter 1 Relations and Functions Ex 1.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.2
Question 1.
Let A = {1, 2, 3, 7} and B = {3, 0, -1, 7}, which of the following are relation from A to B?
(i) R1 = {(2,1), (7,1)}
(ii) R2 = {(-1,1)}
(iii) R3 = {(2,-1), (7, 7), (1,3)}
(iv) R4 = {(7, -1), (0, 3), (3, 3), (0, 7)}
Answer:
A = {1,2,3,7} B = {3,0,-1, 7}
A × B = {1,2,3} × {3, 0,-1, 7}
A × B = {(1,3) (1,0) (1,-1) (1,7) (2,3) (2, 0)
(2, -1) (2, 7) (3, 3) (3,0) (3,-1)
(3, 7) (7, 3) (7, 0) (7,-1) (7, 7)}
(i) R1 = {(2, 1)} (7, 1)
It is not a relation, there is no element of (2, 1) and (7, 1) in A × B
(ii) R2 = {(-1),1)}
It is not a relation, there is no element of
(-1, 1) in A × B
(iii) R3 = {(2,-1) (7, 7) (1,3)}
Yes, It is a relation
(iv) R4 = {(7,-1) (0,3) (3, 3) (0,7)}
It is not a relation, there is no element of (0, 3) and (0, 7) in A × B
![]()
Question 2.
Let A = {1, 2, 3, 4,…,45} and R be the relation defined as “is square of ” on A. Write R as a subset of A × A. Also, find the domain and range of R.
Solution:
A = {1, 2, 3, 4, . . . 45}, A × A = {(1, 1), (2, 2) ….. (45, 45)}
R – is square of’
R = {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25), (6, 36)}
R ⊂ (A × A)
Domain of R = {1, 2, 3, 4, 5, 6}
Range of R = {1, 4, 9, 16, 25, 36}
Question 3.
A Relation R is given by the set {(x, y)/y = x + 3, x ∈ {0, 1, 2, 3, 4, 5}}. Determine its domain and range.
Answer:
x = {0, 1, 2, 3, 4, 5}
y = x + 3
when x = 0 ⇒ y = 0 + 3 = 3
when x = 1 ⇒ y = 1 + 3 = 4
when x = 2 ⇒ y = 2 + 3 = 5
when x = 3 ⇒ y = 3 + 3 = 6
when x = 4 ⇒ y = 4 + 3 = 7
when x = 5 y = 5 + 3 = 8
R = {(0, 3) (1,4) (2, 5) (3, 6) (4, 7) (5, 8)}
Domain = {0, 1, 2, 3, 4, 5}
Range = {3, 4, 5, 6, 7, 8}
![]()
Question 4.
Represent each of the given relations by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible.
(i) {(x,y) | x = 2y,x ∈ {2, 3, 4, 5}, y ∈ {1, 2, 3, 4}
(ii) {(x, y) | y = x + 3, x, y are natural numbers < 10}
Answer:
(i) x = {2, 3, 4, 5} y = {1, 2, 3, 4}
x = 2y
wheny y = 1 ⇒ x = 2 × 1 = 2
when y = 2 ⇒ x = 2 × 2 = 4
when y = 3 ⇒ r = 2 × 3 = 6
when y = 4 ⇒ x = 2 × 4 = 8
(a) Arrow diagram
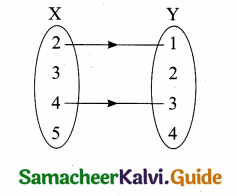
(b) Graph
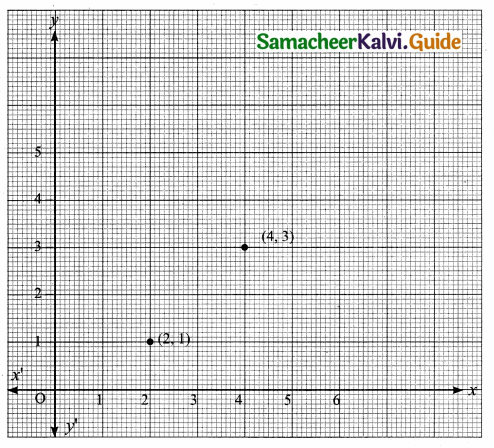
(c) Roster form R = {(2, 1) (4, 3)}
(ii) x = {1, 2, 3, 4, 5, 6, 7, 8, 9}
y = {1,2, 3, 4, 5, 6, 7, 8,9}
y = x + 3
when x = 1 ⇒ y = 1 + 3 = 4
when x = 2 ⇒ y = 2 + 3 = 5
when x = 3 ⇒ y = 3 + 3 = 6
when x = 4 ⇒ y = 4 + 3 = 7
when x = 5 ⇒ y = 5 + 3 = 8
when x = 6 ⇒ y = 6 + 3 = 9
when x = 7 ⇒ y = 7 + 3 = 10
when x = 8 ⇒ y = 8 + 3 = 11
when x = 9 ⇒ y = 9 + 3 = 12
R = {(1,4) (2, 5) (3,6) (4, 7) (5, 8) (6, 9)}
![]()
(a) Arrow diagram
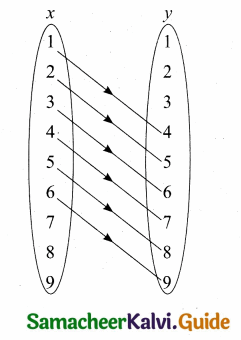
(b) Graph
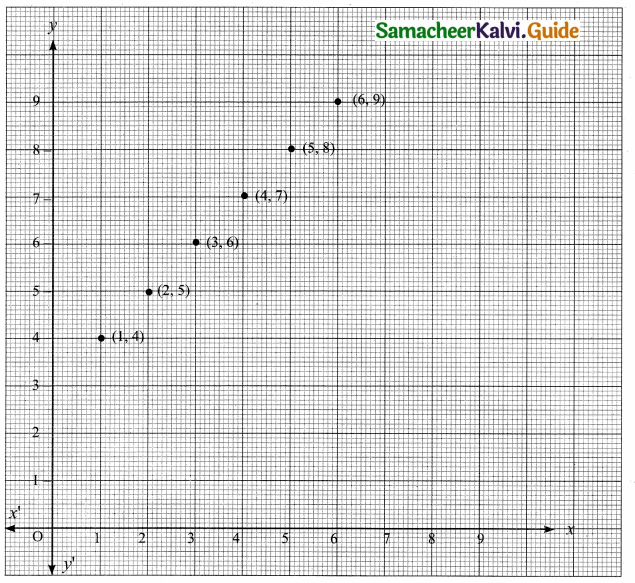
(c) Roster form: R = {(1, 4) (2, 5) (3, 6) (4, 7) (5, 8) (6, 9)}
![]()
Question 5.
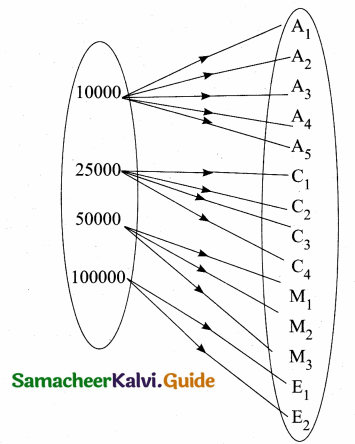
A company has four categories of employees given by Assistants (A), Clerks (C), Managers (M) and an Executive Officer (E). The company provide ₹10,000, ₹25,000, ₹50,000 and ₹1,00,000 as salaries to the people who work in the categories A, C, M and E respectively. If A1, A2, A3, A4 and A5 were Assistants; C1, C2, C3, C4 were Clerks; M1, M2, M3 were managers and E1, E2 were Executive officers and if the relation R is defined by xRy, where x is the salary given to person y, express the relation R through an ordered pair and an arrow diagram.
Answer:
Assistants → A1, A2, A3, A4, A5
Clerks → C1, C2, C3, C4
Managers → M1, M2, M3
Executive officers → E1, E2
R = {00000, A1) (10000, A2) (10000, A3) (10000, A4) (10000, A5)
(25000, C1) (25000, C2) (25000, C3) (25000, C4)
(50000, M1) (50000, M2) (50000, M3) (100000, E1) (100000, E2)}
(a) Arrow diagram
![]()
Functions Definition
A relation f between two non – empty sets X and Y is called a function from X to Y if for each x ∈ X there exists only one Y ∈ Y such that (x, y) ∈ f
f = {(x, y) / for all x ∈ X, y ∈ f}
Note: The range of a function is a subset of its co-domain