Students can download Maths Chapter 2 Numbers and Sequences Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.3
Question 1.
Find the least positive value of x such that
(i) 71 = x (mod 8)
Answer:
71 = 7 (mod 8)
∴ The value of x = 7

(ii) 78 + x = 3 (mod 5)
78 + x – 3 = 5n (n is any integer)
75 + x = 5n
(Let us take x = 5)
75 + 5 = 80 (80 is a multiple of 5)
∴ The least value of x is 5
![]()
(iii) 89 = (x + 3) (mod 4)
89 – (x + 3) = 4n
(n may be any integer)
89 – x – 3 = 4n
89 – x = 4n
86 – x is a multiple of 4
(84 is a multiple of 4)
86 – 2 = 4n
84 = 4n
The value of x is 2
(iv) 96 = \(\frac { x }{ 7 } \) (mod 5)
96 – \(\frac { x }{ 7 } \) = 5n (n may be any integer)
672 – x = 35n (multiple of 35 is 665)
672 – 7 = 665
∴ The value of x = 7
(v) 5x = 4 (mod 6)
5x – 4 = 6n (n may be any integer)
5x = 6n + 4
x = \(\frac { 6n+4 }{ 5 } \)
Substitute the value of n as 1, 6, 11, 16 …. as n values in x = \(\frac { 6n+4 }{ 5 } \) which is divisible by 5.
2, 8, 14, 20,…………
The least positive value is 2.
Question 2.
If x is congruent to 13 modulo 17 then 7x -3 is congruent to which number modulo 17?
Solution:
x ≡ 13 (mod 17)
Let p be the required number …………. (1)
7x – 3 ≡ p (mod 17) ………….. (2)
From (1),
x – 13 = 17n for some integer M.
x – 13 is a multiple of 17.
x must be 30.
∴ 30 – 13 = 17
which is a multiple of 17.
From (2),
7 × 30 – 3 ≡ p (mod 17)
210 – 3 ≡ p (mod 17)
207 ≡ p (mod 17)
207 ≡ 3 (mod 17)
∴ P ≡ 3
![]()
Question 3.
Solve 5x ≡ 4 (mod 6)
5x – 4 = 6n (n may be any integer)
5x = 6n + 4
x = \(\frac{6 n+4}{5}\)
The value of n 1, 6, 11, 16 ……..
∴ The value of x is 2, 8, 14, 20 …………..
Question 4.
Solve 3x – 2 = 0 (mod 11)
Answer:
Given 3x – 2 = 0(mod 11)
3x – 2 = 11n (n may be any integer)
3x = 2 + 11n
x = \(\frac { 11n+2 }{ 3 } \)
Substitute the value of n = 2, 5, 8, 11 ….
When n ≡ 2 ⇒ x = \(\frac { 22+2 }{ 3 } \) = \(\frac { 24 }{ 3 } \) = 8
When n = 5 ⇒ x = \(\frac { 55+2 }{ 3 } \) = \(\frac { 57 }{ 3 } \) = 19
When n = 8 ⇒ x = \(\frac { 88+2 }{ 3 } \) = \(\frac { 90 }{ 3 } \) = 30
When n = 11 ⇒ x = \(\frac { 121+2 }{ 3 } \) = \(\frac { 123 }{ 3 } \) = 41
∴ The value of x is 8, 19, 30,41
Question 5.
What is the time 100 hours after 7 a.m.?
Answer:
100 ≡ x (mod 12) Note: In a clock every 12 hours
100 ≡ 4 (mod 12) the numbers repeats.
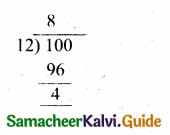
The time repeat after 7 am is 7 + 4 = 11 o’ clock (or) 11 am.
![]()
Question 6.
What is time 15 hours before 11 p.m.?
Solution:
15 ≡ x (mod 12)
15 – x = 12n
15 – x is a multiple of 12 x must be 3.
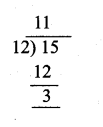
∴ The time 15 hrs before 11 O’clock is 11 – 3 = 8 O’ clock i.e. 8 p.m
Question 7.
Today is Tuesday. My uncle will come after 45 days. In which day my uncle will be coming?
Answer:
Number of days in a week = 7
45 ≡ x (mod 7)
45 ≡ 3 (mod 7)
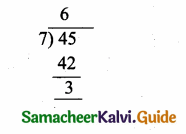
The value of x must be 3.
Three days after tuesday is friday uncle will come on friday.
![]()
Question 8.
Prove that 2n + 6 × 9n is always divisible by 7 for any positive integer n.
Solution:
21 + 6 × 91 = 2 + 54 = 56 is divisible by 7
When n = k,
2k + 6 × 9k = 7 m [where m is a scalar]
⇒ 6 × 9k = 7 m – 2k …………. (1)
Let us prove for n = k + 1
Consider 2k+1 + 6 × 9k+1 = 2k+1 + 6 × 9k × 9
= 2k+1 + (7m – 2k)9 (using (1))
= 2k+1 + 63m – 9.2k = 63m + 2k.21 – 9.2k
= 63m – 2k (9 – 2) = 63m – 7.2k
= 7 (9m – 2k) which is divisible by 7
∴ 2n + 6 × 9n is divisible by 7 for any positive integer n
Question 9.
Find the remainder when 281 is divided by 17?
Answer:
281 ≡ x(mod 17)
240 × 240 × 21 ≡ x(mod 17)
(24)10 × (24)10 × 21 ≡ x(mod 17)
(16)10 × (16)10 × 21 ≡ x(mod 17)
(162)5 × (162)5 × 21 ≡ x(mod 17)
= 1 × 1 × 2 (mod 17)
[(16)2 = 256 = 1 (mod 17)]
= 2 (mod 17)
281 = 2(mod 17)
∴ x = 2
The remainder is 2
![]()
Question 10.
The duration of flight travel from Chennai to London through British Airlines is approximately 11 hours. The airplane begins its journey on Sunday at 23:30 hours. If the time at Chennai is four and half hours ahead to that of London’s time, then find the time at London, when will the flight lands at London Airport?
Answer:
Duration of the flight time = 11 hours
(Chennai to London)
Starting time on Sunday = 23 : 30 hour

Time difference is 4 \(\frac { 1 }{ 2 } \) horns ahead to london
The time to reach London airport = (10.30 – 4.30)
= 6 am
The first reach the london airport next day (monday) at 6 am